Chủ đề trắc nghiệm chuyển động thẳng đều: Trắc nghiệm chuyển động thẳng đều là một phần quan trọng trong chương trình Vật lý lớp 10, giúp học sinh củng cố kiến thức về chuyển động cơ bản. Bài viết này cung cấp các câu hỏi trắc nghiệm phong phú, phân tích chi tiết và lời giải, giúp học sinh ôn tập hiệu quả và chuẩn bị cho các kỳ kiểm tra với kết quả tốt nhất.
Mục lục
Trắc Nghiệm Chuyển Động Thẳng Đều
Chuyển động thẳng đều là một trong những kiến thức cơ bản trong chương trình vật lý trung học phổ thông. Dưới đây là một số bài tập trắc nghiệm phổ biến về chủ đề này, cùng với các công thức và phương pháp giải thích liên quan.
1. Khái Niệm Về Chuyển Động Thẳng Đều
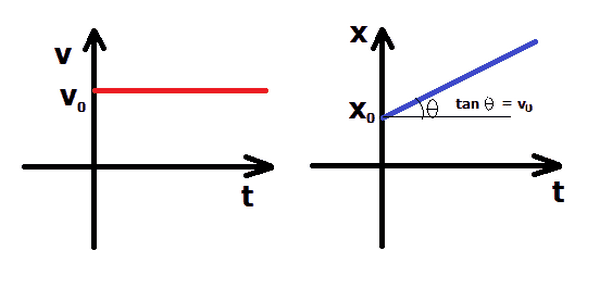
Chuyển động thẳng đều là chuyển động có quỹ đạo là một đường thẳng và tốc độ không thay đổi theo thời gian. Công thức tính quãng đường và vận tốc trong chuyển động thẳng đều được thể hiện qua các công thức sau:
- Quãng đường: \( s = v \cdot t \)
- Vận tốc: \( v = \frac{s}{t} \)
2. Bài Tập Trắc Nghiệm
Dưới đây là một số bài tập trắc nghiệm về chuyển động thẳng đều:
- Một vật chuyển động thẳng đều với vận tốc 20 m/s trong 10 giây. Hỏi vật đi được quãng đường bao nhiêu?
- Đáp án:
- A. 100 m
- B. 200 m
- C. 400 m
- D. 500 m
- Phương trình nào sau đây là phương trình của chuyển động thẳng đều?
- A. \( x = 5 + 10t \)
- B. \( x = 5 + 10t + 0,5t^2 \)
- C. \( x = 10 - 2t + 6t^2 \)
- D. \( x = 4 + 3t - t^2 \)
- A. 1 giờ
- B. 2 giờ
- C. 0.5 giờ
- D. 3 giờ
3. Phương Pháp Giải Các Bài Toán Chuyển Động Thẳng Đều
Để giải các bài toán chuyển động thẳng đều, ta có thể sử dụng các bước cơ bản như sau:
- Xác định các đại lượng liên quan như quãng đường, thời gian, vận tốc.
- Áp dụng các công thức: \( v = \frac{s}{t} \) và \( s = v \cdot t \).
- Suy luận logic dựa trên dữ liệu đề bài cung cấp.
4. Một Số Công Thức Quan Trọng
| Công thức | Giải thích |
| \( v = \frac{s}{t} \) | Tính vận tốc trung bình, trong đó \( v \) là vận tốc, \( s \) là quãng đường và \( t \) là thời gian. |
| \( s = v \cdot t \) | Tính quãng đường đi được với vận tốc \( v \) và thời gian \( t \). |
| \( t = \frac{s}{v} \) | Tính thời gian chuyển động khi biết quãng đường và vận tốc. |
5. Lời Kết
Chuyển động thẳng đều là một chủ đề quan trọng trong vật lý học, cung cấp nền tảng cho các bài toán về động lực học và kinematics. Việc nắm vững các công thức và phương pháp giải sẽ giúp học sinh dễ dàng vượt qua các bài kiểm tra và hiểu rõ hơn về chuyển động trong thực tế.

.png)
1. Khái niệm cơ bản về chuyển động thẳng đều
Chuyển động thẳng đều là một loại chuyển động mà trong đó vận tốc của vật không thay đổi theo thời gian, tức là vật di chuyển với vận tốc không đổi trên một đường thẳng. Đặc điểm chính của chuyển động này là:
- Vận tốc có độ lớn không đổi: \(v = \frac{s}{t}\), trong đó \(s\) là quãng đường đi được và \(t\) là thời gian di chuyển.
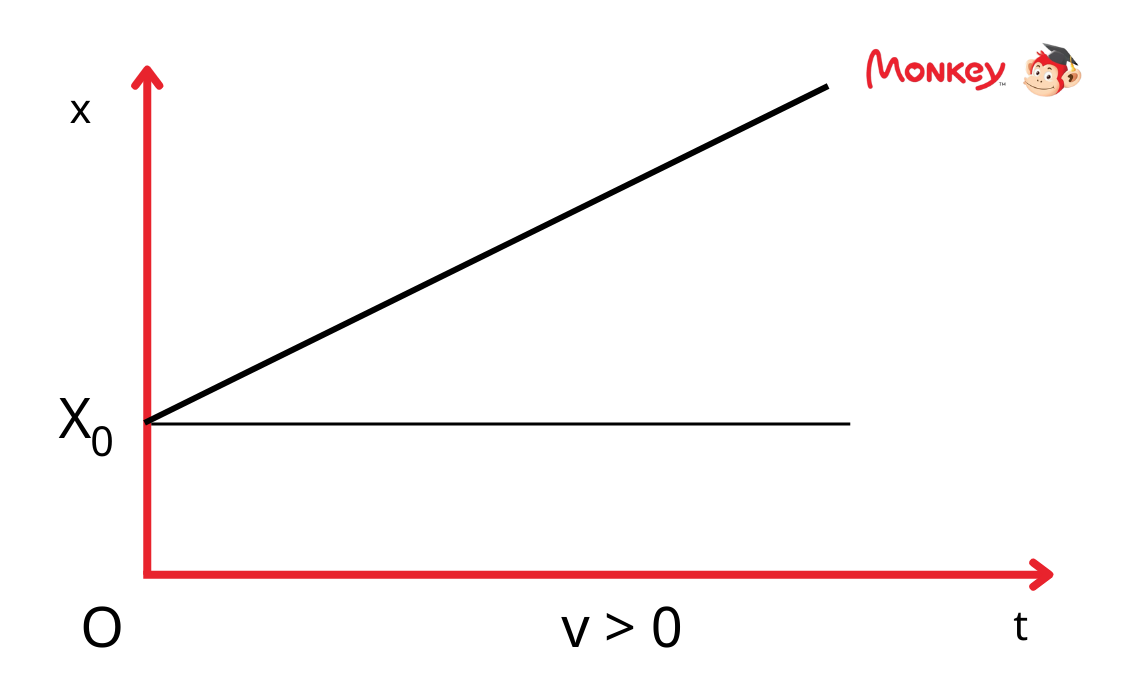
- Phương trình chuyển động có dạng: \(x = x_0 + v \cdot t\), với \(x_0\) là vị trí ban đầu và \(v\) là vận tốc.
- Đồ thị tọa độ theo thời gian của chuyển động thẳng đều là một đường thẳng, vì tọa độ \(x\) là hàm bậc nhất của thời gian.
Ví dụ minh họa:
- Một chiếc xe di chuyển với vận tốc \(40\, \text{km/h}\) trên một quãng đường thẳng trong 2 giờ. Quãng đường xe đã di chuyển được là \(s = v \cdot t = 40 \times 2 = 80\, \text{km}\).
Do vận tốc không đổi nên các chuyển động thẳng đều rất dễ dự đoán và tính toán, đây là một trong những dạng chuyển động đơn giản nhất trong vật lý.
2. Bài tập và trắc nghiệm về chuyển động thẳng đều
Chuyển động thẳng đều là một trong những khái niệm quan trọng trong động học chất điểm, được đưa vào rất nhiều bài tập và trắc nghiệm để giúp học sinh nắm rõ lý thuyết và áp dụng vào thực tế. Phần này sẽ giới thiệu một số dạng bài tập phổ biến cùng với cách giải chi tiết.
- Bài tập tính vận tốc trong chuyển động thẳng đều
- Bài tập xác định quãng đường trong chuyển động thẳng đều
- Bài tập trắc nghiệm với nhiều phương án lựa chọn
- Một người đi bộ với vận tốc không đổi 2 m/s trong 6 phút. Quãng đường người đó đi được là:
- A. 360 m
- B. 720 m
- C. 180 m
- D. 540 m
- Một xe máy đi với vận tốc 20 m/s trong 10 giây. Tính quãng đường xe đã đi được:
- A. 200 m
- B. 100 m
- C. 400 m
- D. 50 m
Cho biết quãng đường và thời gian, học sinh cần tính vận tốc bằng công thức:
\[ v = \frac{s}{t} \]Ví dụ: Một xe ô tô đi được quãng đường 100 m trong 10 giây. Vận tốc của xe là:
\[ v = \frac{100}{10} = 10 \, m/s \]Với vận tốc không đổi, quãng đường được tính bằng công thức:
\[ s = v \cdot t \]Ví dụ: Một người đi bộ với vận tốc 2 m/s trong 5 giây. Quãng đường người đó đi được là:
\[ s = 2 \cdot 5 = 10 \, m \]Trắc nghiệm sẽ cung cấp nhiều phương án để học sinh lựa chọn, ví dụ:

3. Phân tích và so sánh các dạng bài tập chuyển động thẳng đều
Chuyển động thẳng đều là dạng chuyển động cơ bản trong vật lý, với nhiều bài tập áp dụng khác nhau. Dưới đây là các dạng bài tập thường gặp:
- Dạng 1: Xác định vận tốc trung bình
Ở dạng này, bài tập yêu cầu tính toán vận tốc trung bình của một vật di chuyển trong một quãng đường nhất định. Công thức cơ bản là:
\[ v_{tb} = \frac{s}{t} \]Trong đó:
- v_{tb} là vận tốc trung bình.
- s là quãng đường vật đi được.
- t là thời gian vật di chuyển.
- Dạng 2: Viết phương trình chuyển động
Ở dạng bài tập này, người giải phải thiết lập phương trình chuyển động của vật. Với chuyển động thẳng đều, phương trình có dạng:
\[ x = v t + x_0 \]Trong đó:
- x là vị trí của vật tại thời điểm t.
- v là vận tốc không đổi.
- x_0 là vị trí ban đầu của vật.
- Dạng 3: Tìm thời điểm gặp nhau của hai vật chuyển động
Dạng bài tập này yêu cầu tính thời điểm và vị trí mà hai vật chuyển động gặp nhau. Phương pháp giải thường là thiết lập phương trình chuyển động cho từng vật và giải hệ phương trình:
\[ x_1 = x_2 \]Giải phương trình này ta tìm được thời gian và vị trí gặp nhau.

4. Các mẹo và chiến lược giải bài tập trắc nghiệm
Khi giải các bài tập trắc nghiệm về chuyển động thẳng đều, việc nắm vững các mẹo và chiến lược sẽ giúp bạn tiết kiệm thời gian và tránh sai lầm. Dưới đây là một số gợi ý hữu ích:
- Xác định các đại lượng chính: Trước tiên, hãy xác định các đại lượng như vận tốc, thời gian và quãng đường, sử dụng các công thức chính như \( s = v t \).
- Sử dụng phương trình phù hợp: Đối với mỗi dạng bài tập, áp dụng các công thức thích hợp, ví dụ như tính vận tốc trung bình \( v_{tb} = \frac{s}{t} \).
- Loại trừ đáp án sai: Nếu không chắc chắn với một đáp án, hãy sử dụng phương pháp loại trừ các câu trả lời không hợp lý để thu hẹp lựa chọn.
- Chú ý đến đơn vị: Chuyển đổi đơn vị là rất quan trọng, đặc biệt trong bài tập liên quan đến vận tốc và thời gian. Hãy chú ý đổi \( km/h \) sang \( m/s \) khi cần.
Với các mẹo này, bạn sẽ có thể giải quyết các câu hỏi trắc nghiệm về chuyển động thẳng đều một cách dễ dàng và nhanh chóng.

5. Tài liệu tham khảo và nguồn học tập
Để hiểu sâu hơn về chuyển động thẳng đều và các dạng bài tập liên quan, bạn có thể tham khảo các tài liệu và nguồn học tập sau đây:
- Sách giáo khoa Vật lý lớp 10: Đây là nguồn học liệu chính thống, cung cấp các kiến thức cơ bản về chuyển động thẳng đều và các bài tập vận dụng đi kèm.
- Trang web học trực tuyến: Các nền tảng học tập như Olm.vn hoặc VietJack cung cấp các bài tập trắc nghiệm với đáp án chi tiết, giúp bạn luyện tập.
- Video bài giảng: Các kênh YouTube giáo dục như Vật Lý 10 - Cô Hằng có nhiều video giải thích rõ ràng về lý thuyết và cách giải bài tập trắc nghiệm.
- Ứng dụng di động: Ứng dụng như Zuni hoặc Hocmai có các bài kiểm tra và bài giảng tương tác, giúp bạn nắm vững kiến thức.
Việc kết hợp nhiều nguồn tài liệu sẽ giúp bạn tiếp cận kiến thức từ nhiều góc độ và rèn luyện kỹ năng giải quyết các bài tập một cách hiệu quả.