PT chuyển động thẳng đều: Khái niệm, công thức và ứng dụng thực tế

Chuyển động thẳng đều là một dạng chuyển động cơ bản trong vật lý, trong đó vật di chuyển trên quỹ đạo thẳng và vận tốc không đổi theo thời gian. Dưới đây là những thông tin chi tiết về chuyển động thẳng đều, bao gồm định nghĩa, phương trình, và các bài tập minh họa.

Định nghĩa

Chuyển động thẳng đều là chuyển động của một vật trên một đường thẳng với tốc độ trung bình không đổi. Tốc độ trung bình của vật được xác định bởi công thức:

\[v = \frac{s}{t}\]

Trong đó:

• \(v\) là vận tốc của vật
• \(s\) là quãng đường đi được

Phương trình chuyển động thẳng đều

Phương trình tổng quát của chuyển động thẳng đều được viết dưới dạng:

\[x = x_0 + v(t - t_0)\]

Trong đó:

• \(x\) là tọa độ của vật tại thời điểm \(t\)
• \(x_0\) là tọa độ của vật tại thời điểm bắt đầu \(t_0\)
• \(t_0\) là thời điểm bắt đầu chuyển động

Ví dụ minh họa

Xét một vật chuyển động thẳng đều từ điểm \(A\) đến điểm \(B\) với vận tốc \(v = 10\, m/s\). Biết rằng thời điểm bắt đầu là \(t_0 = 0\, s\), tọa độ ban đầu của vật là \(x_0 = 0\, m\). Sau 5 giây, tọa độ của vật là bao nhiêu?

Lời giải:

Sử dụng phương trình chuyển động thẳng đều:

\[x = x_0 + v(t - t_0)\]

Thay các giá trị vào phương trình:

\[x = 0 + 10(5 - 0) = 50\, m\]

Vậy sau 5 giây, vật sẽ ở vị trí cách điểm bắt đầu 50m.

Quãng đường đi được trong chuyển động thẳng đều

Quãng đường vật đi được trong chuyển động thẳng đều được tính theo công thức:

\[s = v \cdot t\]

Trong đó:

• \(t\) là thời gian chuyển động

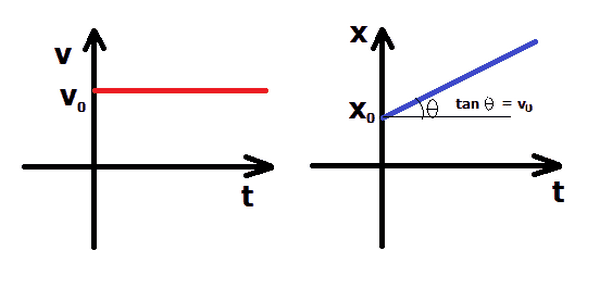
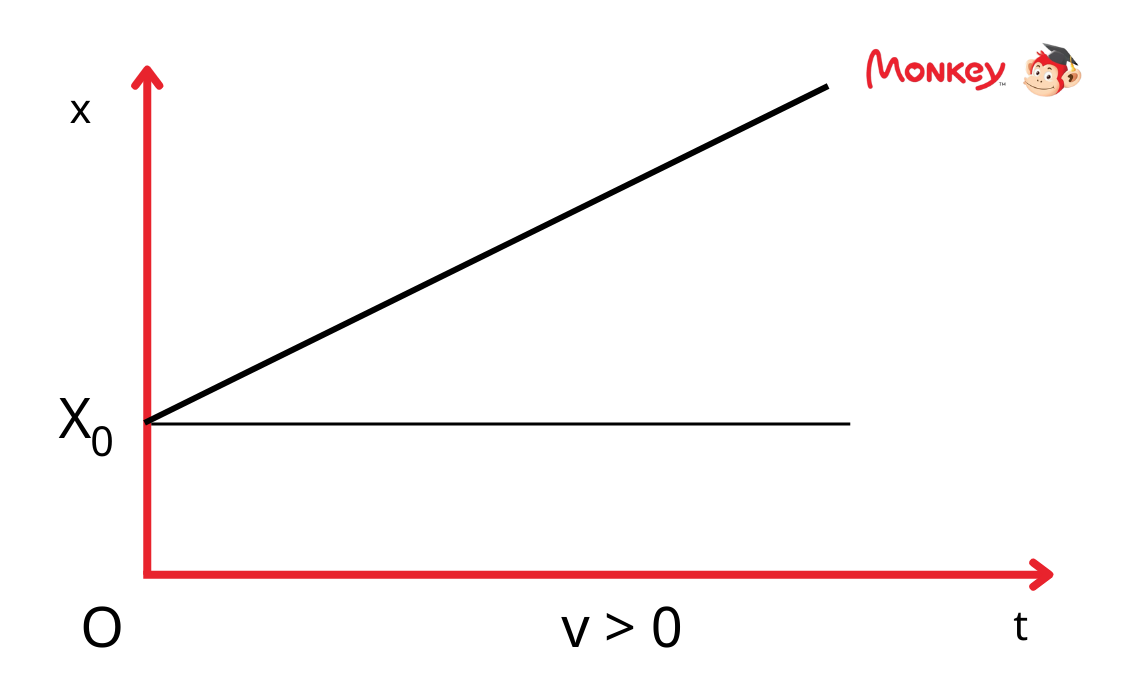
Đồ thị chuyển động thẳng đều

Đồ thị chuyển động thẳng đều trên hệ trục tọa độ thời gian - tọa độ là một đường thẳng với độ dốc bằng vận tốc của vật. Đồ thị này giúp mô tả rõ ràng sự thay đổi vị trí của vật theo thời gian.

\[x = v \cdot t + x_0\]

Bài tập thực hành

Dưới đây là một số bài tập giúp bạn rèn luyện kỹ năng giải bài toán chuyển động thẳng đều:

1. Một xe ô tô xuất phát từ điểm \(A\) với vận tốc \(v = 15\, m/s\). Tính quãng đường xe đi được sau 10 giây.
2. Một vật di chuyển từ điểm \(O\) với vận tốc không đổi \(v = 20\, km/h\). Sau 2 giờ, vật sẽ ở đâu?
3. Viết phương trình chuyển động của một xe bắt đầu từ vị trí \(x_0 = 10\, m\) với vận tốc \(v = 5\, m/s\) sau 8 giây.

Chuyển động thẳng đều là một loại chuyển động trong đó vật di chuyển trên một đường thẳng với vận tốc không đổi theo thời gian. Điều này có nghĩa là quãng đường đi được của vật trong mọi khoảng thời gian là như nhau, không phụ thuộc vào thời điểm bắt đầu. Chuyển động thẳng đều thường được mô tả bởi phương trình:

Trong đó:

• \(x\): Vị trí của vật tại thời điểm \(t\).
• \(x_0\): Vị trí ban đầu của vật (khi \(t = 0\)).
• \(v\): Vận tốc của vật (không đổi).
• \(t\): Thời gian vật chuyển động.

Để hiểu rõ hơn, có thể hình dung vật chuyển động với vận tốc \(v\) không đổi, nghĩa là quãng đường mà vật đi được trong mỗi đơn vị thời gian là không thay đổi. Ví dụ, nếu vật di chuyển với vận tốc \(v = 20\) km/h, thì mỗi giờ nó sẽ di chuyển được 20 km, không thay đổi dù ở thời điểm nào trong hành trình.

Chuyển động thẳng đều thường được gặp trong nhiều bài toán thực tế như xe ô tô di chuyển trên đường thẳng với vận tốc cố định, hoặc các hiện tượng chuyển động trong vật lý cơ bản.

Ví dụ một bài toán về chuyển động thẳng đều:

1. Một ô tô chuyển động thẳng đều từ điểm A đến điểm B với vận tốc 60 km/h. Quãng đường từ A đến B là 120 km. Hãy tính thời gian để ô tô đi từ A đến B?

Giải:

Như vậy, ô tô cần 2 giờ để đi từ A đến B.

Dưới đây là một số bài tập vận dụng về chuyển động thẳng đều, giúp người học nắm vững lý thuyết và phương pháp giải các bài toán liên quan.

• Bài tập 1: Một xe ô tô di chuyển với vận tốc không đổi trên quãng đường 100 km trong thời gian 2 giờ. Tính vận tốc của xe.

Gợi ý: Sử dụng công thức \(v = \frac{s}{t}\), với \(s = 100 \, \text{km}\) và \(t = 2 \, \text{giờ}\).

• Bài tập 2: Một vật chuyển động thẳng đều với vận tốc 20 m/s trong thời gian 10 giây. Tính quãng đường mà vật đi được.

Gợi ý: Sử dụng công thức \(s = v \cdot t\), với \(v = 20 \, \text{m/s}\) và \(t = 10 \, \text{giây}\).

• Bài tập 3: Một xe máy đi từ vị trí \(x_0 = 0\) với vận tốc 15 m/s trong thời gian 5 giây. Tính tọa độ của xe sau 5 giây.

Gợi ý: Sử dụng phương trình chuyển động thẳng đều \(x = x_0 + v \cdot t\), với \(x_0 = 0\), \(v = 15 \, \text{m/s}\), và \(t = 5 \, \text{giây}\).

• Bài tập 4: Một người đi bộ với vận tốc 5 km/h trong 3 giờ. Tính tổng quãng đường mà người này đã đi được.

Gợi ý: Sử dụng công thức \(s = v \cdot t\), với \(v = 5 \, \text{km/h}\) và \(t = 3 \, \text{giờ}\).

• Bài tập 5: Một chiếc xe đạp đi qua hai quãng đường liên tiếp: 50 km với vận tốc 25 km/h và 30 km với vận tốc 20 km/h. Tính vận tốc trung bình của xe trên cả quãng đường.

Gợi ý: Sử dụng công thức tính vận tốc trung bình \(v_{tb} = \frac{s_1 + s_2}{t_1 + t_2}\).

Chuyển động thẳng đều là một trong những loại chuyển động cơ bản và dễ hiểu trong vật lý, ứng dụng của nó hiện diện trong nhiều lĩnh vực của đời sống. Trong thực tế, chuyển động thẳng đều có thể quan sát được ở nhiều phương tiện giao thông như ô tô, tàu hỏa, hoặc máy bay di chuyển trên đường thẳng với vận tốc không đổi.

Dưới đây là một số ứng dụng cụ thể:

• Trong giao thông vận tải: Phương trình chuyển động thẳng đều giúp tính toán vận tốc và khoảng cách giữa các phương tiện, hỗ trợ trong việc điều khiển và lập kế hoạch di chuyển.
• Trong sản xuất công nghiệp: Chuyển động thẳng đều được ứng dụng trong các hệ thống băng chuyền và robot công nghiệp, đảm bảo quá trình sản xuất diễn ra trơn tru và liên tục.
• Trong khoa học và nghiên cứu: Các thí nghiệm vật lý liên quan đến chuyển động của các hạt trong môi trường không trọng lực hay trong chân không thường dựa trên nguyên lý của chuyển động thẳng đều.

Bên cạnh đó, chuyển động thẳng đều còn được áp dụng trong các lĩnh vực đo lường thời gian, không gian và định vị chính xác trong các hệ thống dẫn đường và GPS.

Để giảng dạy và học tập hiệu quả về chuyển động thẳng đều, việc lựa chọn phương pháp phù hợp là rất quan trọng. Giáo viên cần kết hợp các phương pháp như giảng giải, đàm thoại, nêu vấn đề và giải quyết vấn đề. Học sinh cần tham gia vào quá trình học tập thông qua các hoạt động như phân tích bài toán, vẽ đồ thị, và thực hành thí nghiệm.

• Phương pháp phân tích: Giáo viên nên trình bày các khái niệm về chuyển động thẳng đều, ví dụ như vận tốc không đổi và các phương trình liên quan, thông qua việc phân tích các bài toán thực tiễn.
• Phương pháp đàm thoại: Học sinh có thể đặt câu hỏi và thảo luận về các tình huống liên quan đến chuyển động thẳng đều, giúp làm rõ các khái niệm và tăng cường sự tương tác.
• Phương pháp giải quyết vấn đề: Học sinh sẽ được giao các bài tập thực hành để giải quyết những vấn đề liên quan đến chuyển động thẳng đều. Ví dụ, học sinh cần xác định thời gian và quãng đường của các vật thể chuyển động.

Trong quá trình học tập, học sinh cần nắm vững phương trình chuyển động thẳng đều:

Việc vẽ đồ thị và áp dụng các bài toán thực tế sẽ giúp học sinh hiểu sâu hơn về chuyển động này.