Chủ đề bài tập đồ thị chuyển động thẳng đều: Khám phá cách giải quyết các bài tập đồ thị chuyển động thẳng đều với hướng dẫn chi tiết và dễ hiểu. Bài viết này cung cấp các ví dụ thực tiễn, công thức tính toán và hướng dẫn vẽ đồ thị, giúp bạn nắm vững kiến thức và áp dụng hiệu quả vào học tập và công việc.
Mục lục
Bài Tập Đồ Thị Chuyển Động Thẳng Đều
Đồ thị chuyển động thẳng đều là một phần quan trọng trong vật lý, đặc biệt là trong việc hiểu và phân tích chuyển động của các vật thể với vận tốc không đổi. Dưới đây là một số thông tin chi tiết về bài tập liên quan đến đồ thị chuyển động thẳng đều:
1. Khái Niệm Cơ Bản
Chuyển động thẳng đều là loại chuyển động mà trong đó vật thể di chuyển theo một đường thẳng với vận tốc không đổi. Đồ thị của chuyển động thẳng đều thường là một đường thẳng trong hệ tọa độ thời gian và khoảng cách.
2. Công Thức và Đồ Thị
Công thức chính của chuyển động thẳng đều là:
\[ s = v \cdot t \]
Trong đó:
- s là khoảng cách di chuyển.
- v là vận tốc của vật thể.
- t là thời gian di chuyển.
3. Ví Dụ Bài Tập
Dưới đây là một số ví dụ bài tập để áp dụng kiến thức về đồ thị chuyển động thẳng đều:
- Bài Tập 1: Một xe ô tô di chuyển với vận tốc 60 km/h. Tính khoảng cách mà xe ô tô đi được sau 2 giờ.
- Bài Tập 2: Vẽ đồ thị chuyển động của một vật thể di chuyển đều với vận tốc 5 m/s trong 10 giây.
- Bài Tập 3: Xác định vận tốc của một xe đạp nếu đồ thị khoảng cách-thời gian của xe là một đường thẳng với độ dốc 2 m/s.
4. Đồ Thị Ví Dụ
Dưới đây là một ví dụ đồ thị chuyển động thẳng đều:
| Thời Gian (t) | Khoảng Cách (s) |
|---|---|
| 0 | 0 |
| 1 | 10 |
| 2 | 20 |
| 3 | 30 |
Đồ thị từ bảng trên là một đường thẳng, cho thấy mối quan hệ tỷ lệ thuận giữa thời gian và khoảng cách.
5. Ứng Dụng
Hiểu về đồ thị chuyển động thẳng đều giúp học sinh và sinh viên giải quyết các bài toán trong vật lý, đồng thời ứng dụng vào các tình huống thực tiễn trong đời sống và các ngành công nghiệp.

.png)
1. Khái Niệm Về Chuyển Động Thẳng Đều
Chuyển động thẳng đều là một loại chuyển động trong đó một vật thể di chuyển theo một đường thẳng với vận tốc không đổi. Điều này có nghĩa là quãng đường mà vật di chuyển được trong mỗi đơn vị thời gian là như nhau.
Công thức chính của chuyển động thẳng đều:
\[ s = v \cdot t \]
Trong đó:
- s là quãng đường vật di chuyển được (đơn vị: mét).
- v là vận tốc không đổi của vật (đơn vị: mét/giây).
- t là thời gian vật di chuyển (đơn vị: giây).
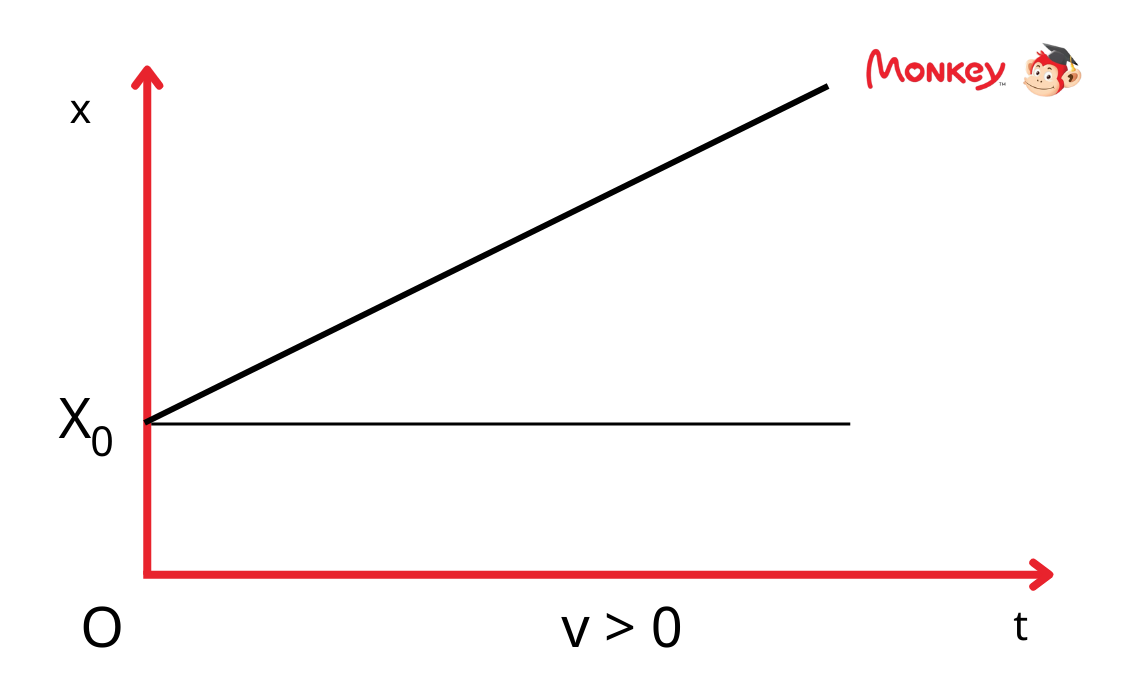
Đồ thị của chuyển động thẳng đều trong hệ tọa độ \((t, s)\) sẽ là một đường thẳng có độ dốc bằng vận tốc của vật thể. Độ dốc càng lớn thì vận tốc càng cao.
Các Đặc Điểm Chính Của Chuyển Động Thẳng Đều:
- Quãng đường di chuyển tỉ lệ thuận với thời gian.
- Vận tốc của vật thể luôn không thay đổi.
- Đồ thị chuyển động thẳng đều là một đường thẳng.
Chuyển động thẳng đều thường được áp dụng trong các bài toán đơn giản về chuyển động, giúp người học dễ dàng hiểu và phân tích các yếu tố như quãng đường, vận tốc, và thời gian.
2. Đồ Thị Chuyển Động Thẳng Đều
Đồ thị chuyển động thẳng đều là một công cụ trực quan giúp ta hiểu rõ hơn về mối quan hệ giữa quãng đường, thời gian và vận tốc của một vật thể di chuyển theo đường thẳng với vận tốc không đổi.
Đồ thị thường được biểu diễn trong hệ tọa độ \((t, s)\), trong đó:
- t là trục thời gian (trục hoành - đơn vị: giây).
- s là trục quãng đường (trục tung - đơn vị: mét).
2.1 Đặc Điểm Của Đồ Thị Chuyển Động Thẳng Đều
- Đồ thị là một đường thẳng đi lên nếu vật chuyển động theo chiều dương và đi xuống nếu vật chuyển động theo chiều âm.
- Độ dốc của đường thẳng chính là vận tốc \((v)\) của vật thể. Công thức biểu diễn độ dốc của đồ thị:
- Nếu đường thẳng càng dốc, vận tốc của vật càng lớn.
- Nếu đồ thị là một đường thẳng nằm ngang, nghĩa là vận tốc bằng 0, vật không di chuyển.
\[ v = \frac{\Delta s}{\Delta t} \]
2.2 Cách Vẽ Đồ Thị Chuyển Động Thẳng Đều
- Xác định các giá trị của quãng đường \((s)\) tại các thời điểm khác nhau \((t)\).
- Chọn hệ tọa độ \((t, s)\) phù hợp, với trục hoành là thời gian và trục tung là quãng đường.
- Vẽ các điểm tương ứng với các cặp giá trị \((t, s)\).
- Nối các điểm lại với nhau để tạo thành đường thẳng đại diện cho chuyển động.
2.3 Phân Tích Đồ Thị Chuyển Động Thẳng Đều
- Nếu đường thẳng có độ dốc lớn, vật di chuyển nhanh.
- Nếu đường thẳng có độ dốc nhỏ, vật di chuyển chậm.
- Nếu độ dốc bằng 0 (đường nằm ngang), vật đứng yên.
Việc phân tích đồ thị giúp học sinh hiểu sâu hơn về mối liên hệ giữa quãng đường, thời gian và vận tốc, từ đó giải quyết các bài toán chuyển động một cách dễ dàng hơn.

3. Công Thức Chuyển Động Thẳng Đều
Chuyển động thẳng đều được mô tả bằng một số công thức cơ bản, giúp tính toán quãng đường, vận tốc, và thời gian trong chuyển động. Dưới đây là các công thức chính:
3.1 Công Thức Tính Khoảng Cách
Khoảng cách \((s)\) mà vật di chuyển được có thể tính bằng:
\[ s = v \cdot t \]
Trong đó:
- s là quãng đường (đơn vị: mét).
- v là vận tốc (đơn vị: mét/giây).
- t là thời gian (đơn vị: giây).
3.2 Công Thức Tính Vận Tốc
Vận tốc \((v)\) của vật trong chuyển động thẳng đều được tính bằng:
\[ v = \frac{s}{t} \]
Trong đó:
- v là vận tốc (đơn vị: mét/giây).
- s là quãng đường (đơn vị: mét).
- t là thời gian (đơn vị: giây).
3.3 Công Thức Tính Thời Gian
Thời gian \((t)\) cần thiết để vật di chuyển một quãng đường \((s)\) với vận tốc \((v)\) được tính bằng:
\[ t = \frac{s}{v} \]
Trong đó:
- t là thời gian (đơn vị: giây).
- s là quãng đường (đơn vị: mét).
- v là vận tốc (đơn vị: mét/giây).
Những công thức này là cơ sở để giải quyết các bài tập liên quan đến chuyển động thẳng đều. Hiểu rõ và áp dụng đúng các công thức này sẽ giúp bạn giải quyết các vấn đề chuyển động một cách hiệu quả và chính xác.
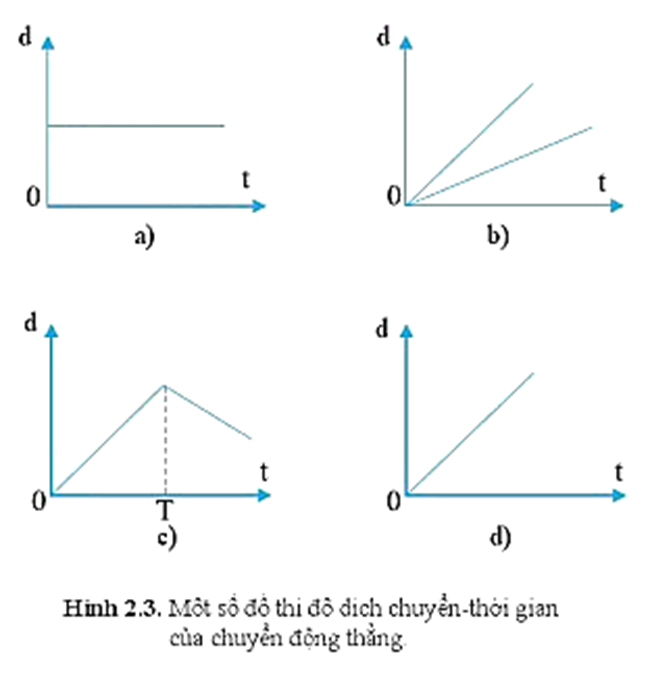
4. Bài Tập Về Chuyển Động Thẳng Đều
Dưới đây là một số bài tập mẫu về chuyển động thẳng đều để giúp bạn luyện tập và củng cố kiến thức. Các bài tập này sẽ bao gồm hướng dẫn chi tiết và giải pháp để bạn dễ dàng theo dõi và áp dụng.
4.1 Bài Tập 1: Tính Quá Trình Di Chuyển
Vật di chuyển với vận tốc 20 m/s. Tính quãng đường vật đi được trong 10 giây.
- Đề bài: Vận tốc \((v) = 20 \text{ m/s}\), Thời gian \((t) = 10 \text{ s}\).
- Giải: Sử dụng công thức \[ s = v \cdot t \], ta có \[ s = 20 \text{ m/s} \times 10 \text{ s} = 200 \text{ m} \].
4.2 Bài Tập 2: Tính Vận Tốc
Vật di chuyển một quãng đường 150 mét trong 5 giây. Tính vận tốc của vật.
- Đề bài: Quãng đường \((s) = 150 \text{ m}\), Thời gian \((t) = 5 \text{ s}\).
- Giải: Sử dụng công thức \[ v = \frac{s}{t} \], ta có \[ v = \frac{150 \text{ m}}{5 \text{ s}} = 30 \text{ m/s} \].
4.3 Bài Tập 3: Tính Thời Gian
Vật có vận tốc 12 m/s và di chuyển một quãng đường 96 mét. Tính thời gian cần thiết để di chuyển quãng đường này.
- Đề bài: Vận tốc \((v) = 12 \text{ m/s}\), Quãng đường \((s) = 96 \text{ m}\).
- Giải: Sử dụng công thức \[ t = \frac{s}{v} \], ta có \[ t = \frac{96 \text{ m}}{12 \text{ m/s}} = 8 \text{ s} \].
4.4 Bài Tập 4: Đồ Thị Chuyển Động
Vẽ đồ thị chuyển động của vật di chuyển với vận tốc không đổi 25 m/s trong thời gian 8 giây. Xác định quãng đường và phân tích đồ thị.
- Đề bài: Vận tốc \((v) = 25 \text{ m/s}\), Thời gian \((t) = 8 \text{ s}\).
- Giải: Tính quãng đường \((s) = v \cdot t = 25 \text{ m/s} \times 8 \text{ s} = 200 \text{ m}\).
- Vẽ đồ thị với trục thời gian \((t)\) và quãng đường \((s)\). Đồ thị là một đường thẳng với độ dốc bằng vận tốc 25 m/s.
Việc thực hành các bài tập này sẽ giúp bạn củng cố kiến thức về chuyển động thẳng đều và nâng cao khả năng giải quyết các bài toán liên quan.

5. Ứng Dụng Của Chuyển Động Thẳng Đều
Chuyển động thẳng đều có nhiều ứng dụng quan trọng trong đời sống và khoa học. Dưới đây là một số ứng dụng tiêu biểu của loại chuyển động này:
5.1 Ứng Dụng Trong Giao Thông
Chuyển động thẳng đều là một khái niệm cơ bản trong giao thông. Ví dụ, khi một chiếc xe ô tô di chuyển với vận tốc không đổi trên một đoạn đường, chúng ta có thể sử dụng công thức của chuyển động thẳng đều để dự đoán thời gian di chuyển và quãng đường còn lại.
- Ưu điểm: Giúp lên kế hoạch hành trình hiệu quả.
- Ứng dụng: Xác định thời gian đến đích, lập kế hoạch lộ trình.
5.2 Ứng Dụng Trong Kỹ Thuật
Trong kỹ thuật, đặc biệt là trong các thiết bị cơ khí, chuyển động thẳng đều thường được áp dụng để thiết kế các cơ cấu chuyển động với vận tốc ổn định.
- Ưu điểm: Tăng cường độ chính xác và hiệu suất của máy móc.
- Ứng dụng: Hệ thống truyền động, thiết bị đo lường.
5.3 Ứng Dụng Trong Khoa Học Vật Lý
Chuyển động thẳng đều là một phần quan trọng trong nghiên cứu vật lý. Các nhà khoa học sử dụng lý thuyết này để hiểu rõ hơn về các hiện tượng cơ học và thực hiện các thí nghiệm.
- Ưu điểm: Cung cấp nền tảng cho các nghiên cứu và thí nghiệm.
- Ứng dụng: Phân tích chuyển động, nghiên cứu động lực học.
5.4 Ứng Dụng Trong Giáo Dục
Trong giáo dục, việc dạy và học về chuyển động thẳng đều giúp học sinh và sinh viên hiểu rõ hơn về các nguyên lý cơ bản của vật lý. Điều này không chỉ giúp trong việc giải bài tập mà còn trong việc áp dụng kiến thức vào thực tiễn.
- Ưu điểm: Cải thiện khả năng giải quyết vấn đề và tư duy logic.
- Ứng dụng: Bài tập thực hành, dự án nghiên cứu.
Việc hiểu và áp dụng chuyển động thẳng đều trong các lĩnh vực này không chỉ giúp nâng cao kiến thức mà còn cải thiện các kỹ năng thực tế trong nhiều tình huống khác nhau.