Chủ đề thế nào là chuyển động thẳng đều: Chuyển động thẳng đều là một trong những khái niệm cơ bản trong vật lý học, giúp hiểu rõ về cách thức vật thể di chuyển với vận tốc không đổi trên quãng đường thẳng. Trong bài viết này, chúng tôi sẽ giải thích chi tiết về định nghĩa, công thức tính toán, cũng như các ví dụ minh họa sinh động để giúp bạn nắm vững khái niệm này một cách dễ dàng và thú vị.
Mục lục
Chuyển Động Thẳng Đều: Định Nghĩa và Các Đặc Điểm
Chuyển động thẳng đều là một khái niệm cơ bản trong vật lý, thường được giảng dạy ở cấp trung học phổ thông. Đây là dạng chuyển động mà trong đó một vật thể di chuyển theo một đường thẳng với vận tốc không đổi.
Định Nghĩa
Chuyển động thẳng đều là loại chuyển động trong đó vật thể di chuyển trên một đường thẳng và có vận tốc tức thời không thay đổi. Điều này có nghĩa là gia tốc của vật thể bằng không và vận tốc của nó không đổi trong suốt thời gian chuyển động.
Các Đặc Điểm Của Chuyển Động Thẳng Đều
- Quỹ đạo: Đường thẳng.
- Vận tốc: Không đổi trong suốt quá trình chuyển động.
- Gia tốc: Bằng không, vì vận tốc không thay đổi.
Công Thức và Phương Trình
Để mô tả chuyển động thẳng đều, người ta sử dụng các công thức sau:
| Đại lượng | Công thức | Giải thích |
|---|---|---|
| Vận tốc | \( v = \frac{s}{t} \) | Vận tốc bằng quãng đường chia cho thời gian. |
| Quãng đường | \( s = v \cdot t \) | Quãng đường là tích của vận tốc và thời gian. |
| Phương trình chuyển động | \( x = x_0 + v(t - t_0) \) | Tọa độ của vật tại thời điểm \( t \) được tính từ tọa độ ban đầu và vận tốc. |
Ví Dụ Minh Họa
Giả sử một xe ô tô di chuyển trên một con đường thẳng với vận tốc không đổi là 60 km/h. Nếu xe bắt đầu từ điểm A và sau 2 giờ, xe sẽ ở điểm B. Quá trình di chuyển của xe là một ví dụ về chuyển động thẳng đều.
Đồ Thị
Đồ thị của chuyển động thẳng đều thường là một đường thẳng trong hệ tọa độ với trục hoành là thời gian và trục tung là quãng đường. Độ dốc của đường thẳng này tương ứng với vận tốc của vật thể.
Chuyển động thẳng đều là một khái niệm rất quan trọng trong vật lý, giúp hiểu rõ hơn về các dạng chuyển động cơ bản và các mối quan hệ giữa các đại lượng như vận tốc, quãng đường và thời gian.
.png)
1. Định nghĩa chuyển động thẳng đều
Chuyển động thẳng đều là dạng chuyển động trong đó một vật thể di chuyển trên một đường thẳng với vận tốc không đổi theo thời gian. Điều này có nghĩa là quãng đường mà vật đi được tỉ lệ thuận với thời gian di chuyển, và không có sự thay đổi về vận tốc hay hướng di chuyển.
Trong chuyển động thẳng đều, gia tốc của vật bằng 0 vì không có sự thay đổi vận tốc. Công thức cơ bản mô tả chuyển động này là:
- Vận tốc trung bình: \[ v = \frac{s}{t} \]
- Quãng đường: \[ s = v \cdot t \]
- Phương trình chuyển động: \[ x = x_0 + v(t - t_0) \]
Trong đó:
- \( v \) là vận tốc không đổi của vật (m/s)
- \( s \) là quãng đường di chuyển (m)
- \( t \) là thời gian di chuyển (s)
- \( x \) là vị trí của vật tại thời điểm \( t \)
- \( x_0 \) là vị trí ban đầu của vật tại thời điểm \( t_0 \)
Chuyển động thẳng đều là một khái niệm cơ bản trong vật lý, giúp hiểu rõ hơn về các loại chuyển động và các yếu tố liên quan như vận tốc và quãng đường.
2. Công thức tính vận tốc trong chuyển động thẳng đều
Trong chuyển động thẳng đều, vận tốc là một đại lượng không đổi và được xác định bằng cách chia quãng đường di chuyển cho thời gian di chuyển. Dưới đây là các công thức cơ bản để tính vận tốc trong chuyển động thẳng đều:
- Vận tốc trung bình: \[ v = \frac{s}{t} \]
Trong đó, \( v \) là vận tốc trung bình, \( s \) là quãng đường di chuyển và \( t \) là thời gian di chuyển.
- Quãng đường di chuyển: \[ s = v \cdot t \]
Quãng đường \( s \) là tích của vận tốc \( v \) và thời gian \( t \).
- Phương trình chuyển động: \[ x = x_0 + v(t - t_0) \]
Trong phương trình này, \( x \) là vị trí của vật tại thời điểm \( t \), \( x_0 \) là vị trí ban đầu tại thời điểm \( t_0 \), và \( v \) là vận tốc không đổi.
Ví dụ minh họa
Giả sử một xe ô tô di chuyển trên một đoạn đường thẳng với vận tốc không đổi là 80 km/h. Nếu xe di chuyển trong 2 giờ, quãng đường đi được được tính như sau:
| Đại lượng | Giá trị | Công thức |
|---|---|---|
| Vận tốc (v) | 80 km/h | |
| Thời gian (t) | 2 giờ | |
| Quãng đường (s) | 160 km | \[ s = v \cdot t = 80 \text{ km/h} \times 2 \text{ h} \] |
Như vậy, quãng đường di chuyển của xe là 160 km, tính bằng cách nhân vận tốc với thời gian di chuyển. Công thức này giúp bạn dễ dàng tính toán và áp dụng trong nhiều tình huống thực tế.

3. Đồ thị của chuyển động thẳng đều
Trong chuyển động thẳng đều, đồ thị mô tả mối quan hệ giữa các đại lượng như quãng đường, vận tốc và thời gian rất quan trọng để hiểu rõ hơn về tính chất của chuyển động. Có hai loại đồ thị chính thường được sử dụng:
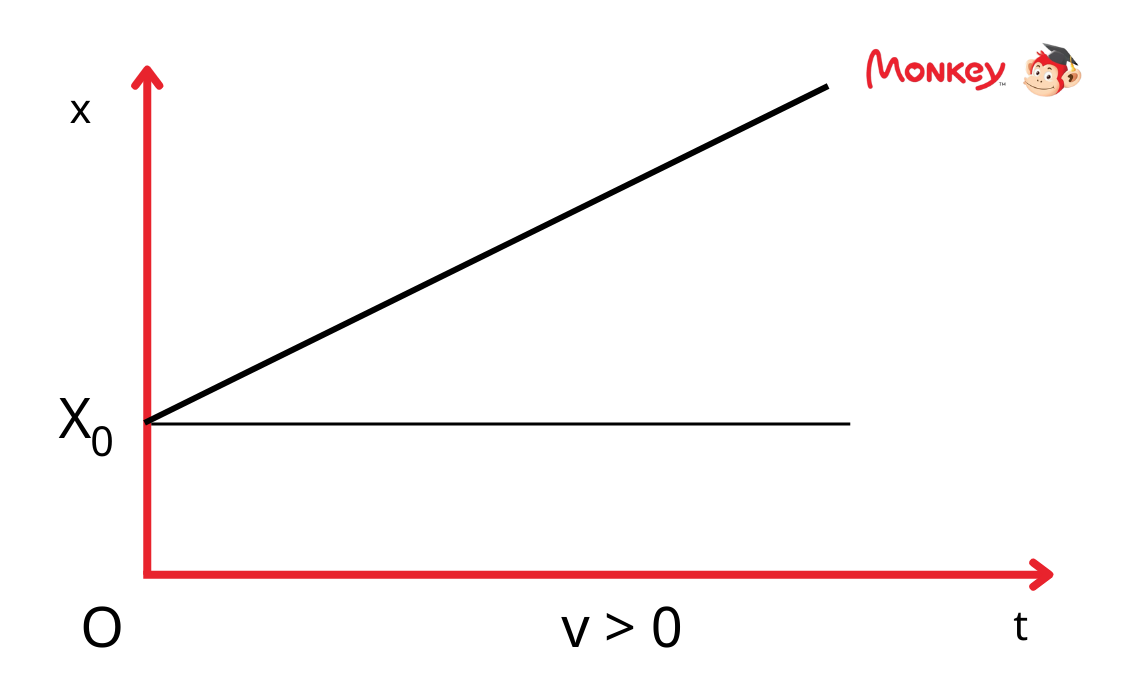
3.1 Đồ thị quãng đường - thời gian
Đồ thị quãng đường - thời gian thể hiện mối quan hệ giữa quãng đường di chuyển và thời gian. Đối với chuyển động thẳng đều, đồ thị này là một đường thẳng có độ dốc không đổi. Độ dốc của đường thẳng chính là vận tốc của vật.
Công thức biểu diễn đồ thị quãng đường - thời gian là:
- Phương trình đồ thị: \[ s = v \cdot t \]
- Trong đó, \( s \) là quãng đường, \( v \) là vận tốc không đổi và \( t \) là thời gian.
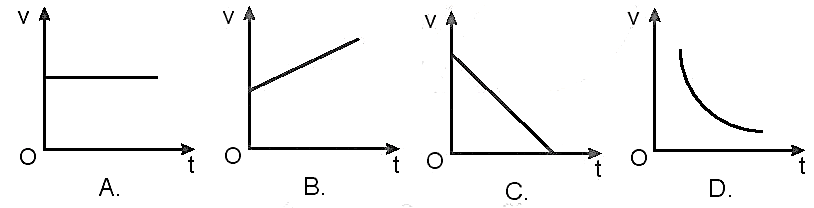
3.2 Đồ thị vận tốc - thời gian
Đối với chuyển động thẳng đều, đồ thị vận tốc - thời gian là một đường nằm ngang, phản ánh vận tốc không thay đổi theo thời gian. Đường thẳng này nằm ở mức vận tốc cố định.
Công thức biểu diễn đồ thị vận tốc - thời gian là:
- Phương trình đồ thị: \[ v = \text{hằng số} \]
- Trong đó, \( v \) là vận tốc không đổi.
Ví dụ minh họa
Giả sử một xe chạy với vận tốc không đổi là 60 km/h. Đồ thị quãng đường - thời gian sẽ là một đường thẳng với độ dốc 60 km/h, trong khi đồ thị vận tốc - thời gian sẽ là một đường ngang ở mức 60 km/h.
| Loại đồ thị | Mô tả |
|---|---|
| Quãng đường - Thời gian | Đường thẳng với độ dốc bằng vận tốc. |
| Vận tốc - Thời gian | Đường ngang phản ánh vận tốc không đổi. |
Những đồ thị này giúp bạn dễ dàng hình dung và phân tích chuyển động thẳng đều trong các tình huống khác nhau.

4. Ví dụ về chuyển động thẳng đều
Đồ thị của chuyển động thẳng đều giúp chúng ta hình dung mối quan hệ giữa các đại lượng quãng đường, thời gian và vận tốc. Có hai loại đồ thị cơ bản trong chuyển động thẳng đều:
3.1 Đồ thị quãng đường - thời gian
Trong đồ thị này, trục hoành (trục x) biểu thị thời gian \( t \), còn trục tung (trục y) biểu thị quãng đường \( s \). Đặc điểm của đồ thị quãng đường - thời gian trong chuyển động thẳng đều là một đường thẳng nghiêng lên, cho thấy quãng đường di chuyển tỉ lệ thuận với thời gian. Công thức của quãng đường trong chuyển động thẳng đều là:
- Đường thẳng này có độ dốc bằng vận tốc \( v \). Vận tốc càng lớn thì độ dốc của đồ thị càng lớn.
- Quãng đường \( s \) tăng đều theo thời gian \( t \), vì vậy đồ thị có dạng một đường thẳng đi lên.
Ví dụ: Nếu một chiếc xe di chuyển với vận tốc \( 20 \, \text{m/s} \), đồ thị quãng đường - thời gian sẽ là một đường thẳng với độ dốc tương ứng với vận tốc này.
3.2 Đồ thị vận tốc - thời gian
Trong đồ thị này, trục hoành (trục x) biểu thị thời gian \( t \), còn trục tung (trục y) biểu thị vận tốc \( v \). Đồ thị vận tốc - thời gian của chuyển động thẳng đều là một đường thẳng nằm ngang, thể hiện rằng vận tốc không thay đổi theo thời gian. Điều này được biểu diễn bằng công thức:
- Đường thẳng nằm ngang chứng tỏ rằng vận tốc \( v \) không thay đổi trong suốt quá trình chuyển động.
- Nếu vận tốc của vật là \( 10 \, \text{m/s} \), đường thẳng trên đồ thị sẽ nằm ở vị trí \( v = 10 \, \text{m/s} \) trên trục tung.
Ví dụ: Khi một vật di chuyển với vận tốc không đổi là \( 5 \, \text{m/s} \), đồ thị vận tốc - thời gian sẽ là một đường thẳng nằm ngang tại mức \( 5 \, \text{m/s} \) trên trục vận tốc.

5. Phân biệt giữa chuyển động thẳng đều và chuyển động thẳng biến đổi đều
Chuyển động thẳng đều và chuyển động thẳng biến đổi đều là hai khái niệm cơ bản trong cơ học. Dưới đây là sự phân biệt chi tiết giữa chúng:
-
5.1 Sự khác nhau giữa hai loại chuyển động
Chuyển động thẳng đều: Là loại chuyển động trong đó vật chuyển động theo một đường thẳng với vận tốc không đổi. Điều này có nghĩa là vật di chuyển một quãng đường bằng nhau trong những khoảng thời gian bằng nhau. Công thức mô tả chuyển động thẳng đều là:
\[ v = \frac{S}{t} \]
Trong đó, \( v \) là vận tốc, \( S \) là quãng đường, và \( t \) là thời gian.
Chuyển động thẳng biến đổi đều: Là loại chuyển động trong đó vật chuyển động theo một đường thẳng nhưng vận tốc thay đổi đều theo thời gian. Vận tốc của vật thay đổi với một gia tốc không đổi. Công thức mô tả chuyển động thẳng biến đổi đều là:
\[ v = u + at \]
\[ S = ut + \frac{1}{2}at^2 \]
Trong đó, \( u \) là vận tốc ban đầu, \( a \) là gia tốc, và \( t \) là thời gian.
-
5.2 Cách nhận biết từng loại chuyển động
Đối với chuyển động thẳng đều: Đồ thị quãng đường - thời gian là một đường thẳng với độ dốc không đổi, cho thấy vận tốc không thay đổi. Đồ thị vận tốc - thời gian là một đường ngang, chứng tỏ vận tốc không thay đổi theo thời gian.
Đối với chuyển động thẳng biến đổi đều: Đồ thị quãng đường - thời gian có hình dạng parabol, cho thấy quãng đường thay đổi theo thời gian theo một quy luật bậc hai. Đồ thị vận tốc - thời gian là một đường thẳng nghiêng, cho thấy vận tốc thay đổi đều theo thời gian.