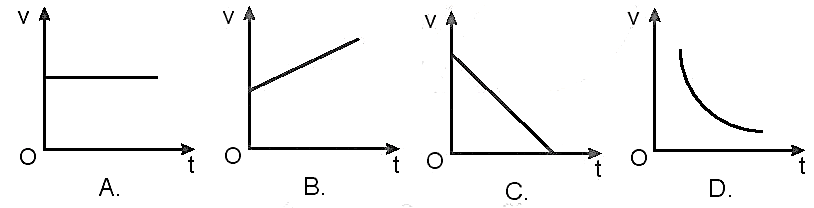
Chủ đề chuyển động thẳng chậm dần đều nhất thiết phải có: Chuyển động thẳng chậm dần đều là một trong những khái niệm cơ bản nhưng quan trọng trong vật lý học. Bài viết này sẽ giúp bạn hiểu rõ nguyên lý hoạt động, các yếu tố cần thiết và ứng dụng thực tiễn của chuyển động thẳng chậm dần đều trong cuộc sống hàng ngày và khoa học kỹ thuật.
Mục lục
- Thông Tin Chi Tiết về Chuyển Động Thẳng Chậm Dần Đều
- Giới thiệu về chuyển động thẳng chậm dần đều
- Các đặc điểm chính của chuyển động thẳng chậm dần đều
- Ứng dụng của chuyển động thẳng chậm dần đều
- Phân tích chuyên sâu về chuyển động thẳng chậm dần đều
- Những vấn đề thường gặp và cách khắc phục
- Tài liệu tham khảo và nguồn học liệu
Thông Tin Chi Tiết về Chuyển Động Thẳng Chậm Dần Đều
Chuyển động thẳng chậm dần đều là một khái niệm cơ bản trong vật lý, thuộc chương trình giáo dục phổ thông. Dưới đây là các thông tin chi tiết về chủ đề này:
1. Khái Niệm Cơ Bản
Chuyển động thẳng chậm dần đều là loại chuyển động trong đó một vật di chuyển theo một đường thẳng với gia tốc không đổi, nhưng gia tốc có giá trị âm. Điều này có nghĩa là vận tốc của vật giảm dần theo thời gian.
2. Các Điều Kiện Cần Có
- Gia tốc âm: Để chuyển động thẳng chậm dần đều, gia tốc phải có giá trị âm, thể hiện rằng vận tốc giảm dần.
- Vận tốc đầu khác không: Vật phải có vận tốc ban đầu khác không để có thể xảy ra chuyển động chậm dần đều.
- Quỹ đạo lớn hơn kích thước vật: Quá trình này thường giả định rằng quỹ đạo chuyển động của vật lớn hơn nhiều lần so với kích thước của nó.
3. Các Phương Trình Chính
Các phương trình cơ bản liên quan đến chuyển động thẳng chậm dần đều bao gồm:
- Phương trình vận tốc: \( v = u + at \), trong đó \( v \) là vận tốc tại thời điểm \( t \), \( u \) là vận tốc ban đầu, và \( a \) là gia tốc.
- Phương trình quãng đường: \( s = ut + \frac{1}{2}at^2 \), trong đó \( s \) là quãng đường di chuyển trong thời gian \( t \).
4. Ví Dụ Thực Tế
Trong thực tế, chuyển động thẳng chậm dần đều có thể thấy ở nhiều tình huống như xe hơi phanh gấp, vật thể rơi tự do từ trên cao với lực cản không khí, hay khi một vật ném lên với gia tốc trọng trường.
5. Ứng Dụng và Ý Nghĩa
Hiểu rõ về chuyển động thẳng chậm dần đều giúp học sinh nắm bắt các khái niệm cơ bản trong vật lý và có thể áp dụng vào các bài tập thực tế cũng như trong các tình huống giao thông hàng ngày.
| Khái Niệm | Ý Nghĩa |
|---|---|
| Gia tốc âm | Vận tốc giảm dần |
| Vận tốc đầu khác không | Có chuyển động bắt đầu |
| Quỹ đạo lớn hơn kích thước vật | Chuyển động có thể được xem xét trong một không gian lớn hơn |
.png)
Giới thiệu về chuyển động thẳng chậm dần đều
Chuyển động thẳng chậm dần đều là một dạng chuyển động cơ học, trong đó vận tốc của vật giảm dần đều theo thời gian trên một đường thẳng. Đây là một khái niệm quan trọng trong vật lý, được ứng dụng trong nhiều lĩnh vực như giao thông, cơ khí và kỹ thuật. Để hiểu rõ hơn về loại chuyển động này, ta cần xem xét các đặc điểm và phương trình cơ bản.
- Đặc điểm chính: Trong chuyển động thẳng chậm dần đều, gia tốc luôn có giá trị âm, nghĩa là nó có xu hướng giảm vận tốc của vật.
- Vận tốc: Vận tốc của vật giảm dần với gia tốc có độ lớn không đổi.
- Phương trình vận tốc:
\[
v = v_0 - a t
\]
Trong đó:
- \(v_0\): Vận tốc ban đầu (m/s)
- \(a\): Gia tốc (m/s²)
- \(t\): Thời gian (s)
- Phương trình quãng đường:
\[
s = v_0 t - \frac{1}{2} a t^2
\]
Trong đó:
- \(s\): Quãng đường (m)
- \(v_0\): Vận tốc ban đầu (m/s)
- \(a\): Gia tốc (m/s²)
- \(t\): Thời gian (s)
Với những phương trình này, ta có thể tính toán vận tốc, quãng đường của vật tại mỗi thời điểm cụ thể trong quá trình chuyển động thẳng chậm dần đều. Điều này giúp chúng ta hiểu rõ hơn cách mà vật chậm lại trong một khoảng thời gian nhất định.
Các đặc điểm chính của chuyển động thẳng chậm dần đều
Chuyển động thẳng chậm dần đều có những đặc điểm nổi bật giúp chúng ta phân biệt nó với các loại chuyển động khác. Dưới đây là các đặc điểm chính của loại chuyển động này:
- Vận tốc giảm đều: Vận tốc của vật giảm dần theo thời gian với một gia tốc không đổi. Điều này có nghĩa là vật đang mất đi động năng và tiến dần đến trạng thái nghỉ.
- Gia tốc âm: Gia tốc trong chuyển động thẳng chậm dần đều luôn là một hằng số âm, nghĩa là nó có giá trị ngược với chiều chuyển động. Gia tốc này làm giảm vận tốc của vật:
\[
a = \frac{\Delta v}{\Delta t} < 0
\]
Trong đó:
- \(a\): Gia tốc (m/s²)
- \(\Delta v\): Sự thay đổi vận tốc (m/s)
- \(\Delta t\): Thời gian thay đổi (s)
- Phương trình vận tốc: Vận tốc tại một thời điểm \(t\) có thể được tính bằng công thức:
\[
v = v_0 - a t
\]
Với:
- \(v\): Vận tốc tại thời điểm \(t\) (m/s)
- \(v_0\): Vận tốc ban đầu (m/s)
- \(a\): Gia tốc (m/s²)
- \(t\): Thời gian (s)
- Phương trình quãng đường: Quãng đường đi được trong khoảng thời gian \(t\) được tính theo công thức:
\[
s = v_0 t - \frac{1}{2} a t^2
\]
Trong đó:
- \(s\): Quãng đường đi được (m)
- \(v_0\): Vận tốc ban đầu (m/s)
- \(a\): Gia tốc (m/s²)
- \(t\): Thời gian (s)
- Thời gian dừng: Khi vận tốc của vật bằng 0, vật dừng lại hoàn toàn. Thời gian để vật dừng lại được tính bằng công thức: \[ t_{\text{dừng}} = \frac{v_0}{a} \] Điều này giúp xác định khoảng thời gian cần thiết để vật chấm dứt chuyển động hoàn toàn.
Những đặc điểm này là cơ sở để phân tích và giải quyết các bài toán liên quan đến chuyển động thẳng chậm dần đều, giúp chúng ta hiểu rõ hơn về cách vật thể giảm vận tốc và dừng lại.

Ứng dụng của chuyển động thẳng chậm dần đều
Chuyển động thẳng chậm dần đều có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật. Các nguyên lý của loại chuyển động này được áp dụng trong nhiều lĩnh vực khác nhau, từ giao thông đến công nghệ sản xuất. Dưới đây là một số ứng dụng tiêu biểu:
- Phanh xe ô tô và xe máy: Khi một phương tiện giao thông như ô tô hoặc xe máy dừng lại, quá trình phanh làm cho chuyển động của xe trở thành chuyển động thẳng chậm dần đều. Gia tốc âm giúp phương tiện giảm dần tốc độ cho đến khi dừng hoàn toàn.
- Hệ thống thang máy: Trong thang máy, khi di chuyển lên hoặc xuống và gần đến tầng yêu cầu, thang máy thường giảm tốc độ để tránh va chạm mạnh. Đây là ứng dụng điển hình của chuyển động thẳng chậm dần đều nhằm đảm bảo an toàn cho hành khách.
- Dừng tàu hỏa: Tàu hỏa khi đến ga thường phải giảm tốc độ một cách từ từ. Quá trình này tuân theo quy luật của chuyển động thẳng chậm dần đều, giúp tàu dừng lại an toàn mà không gây ra sự chấn động mạnh.
- Thiết kế đường dốc: Các con đường dốc trên đèo núi hoặc đường dốc dẫn lên cầu thường được thiết kế để xe giảm tốc độ tự nhiên theo chuyển động thẳng chậm dần đều, nhằm đảm bảo an toàn cho các phương tiện.
- Hệ thống đóng mở cửa tự động: Trong các hệ thống cửa tự động, chuyển động của cửa khi đóng lại thường giảm dần tốc độ trước khi đóng hẳn. Điều này đảm bảo an toàn và tránh gây ra va đập mạnh.
Chuyển động thẳng chậm dần đều là cơ sở cho nhiều ứng dụng kỹ thuật và công nghệ trong cuộc sống, đặc biệt trong việc điều khiển tốc độ và đảm bảo an toàn trong các hệ thống di chuyển và vận hành.

XEM THÊM:
Phân tích chuyên sâu về chuyển động thẳng chậm dần đều
Chuyển động thẳng chậm dần đều là một dạng chuyển động cơ học mà ở đó vận tốc của vật giảm dần đều theo thời gian. Phân tích chuyên sâu về loại chuyển động này đòi hỏi chúng ta phải nắm rõ các phương trình liên quan đến vận tốc, quãng đường, và gia tốc cũng như ý nghĩa vật lý của chúng. Dưới đây là các phân tích chi tiết:
- Vận tốc tức thời: Vận tốc của vật tại thời điểm \(t\) được xác định bằng phương trình: \[ v = v_0 - a t \] Điều này có nghĩa là vận tốc sẽ giảm đều với tốc độ bằng gia tốc \(a\) trong suốt quá trình chuyển động. Nếu \(a > 0\), vật sẽ giảm tốc, và nếu \(v = 0\), vật sẽ dừng lại hoàn toàn.
- Gia tốc không đổi: Gia tốc trong chuyển động thẳng chậm dần đều là một hằng số âm, điều này làm cho vận tốc giảm dần. Gia tốc không đổi cũng dẫn đến sự thay đổi tuyến tính của vận tốc theo thời gian: \[ a = \frac{\Delta v}{\Delta t} \] Đây là yếu tố quan trọng trong việc dự đoán sự thay đổi vận tốc của vật khi thời gian trôi qua.
- Phương trình quãng đường: Quãng đường đi được trong thời gian \(t\) của vật có thể được tính bằng công thức: \[ s = v_0 t - \frac{1}{2} a t^2 \] Phương trình này cho phép chúng ta xác định được quãng đường vật đã đi trong quá trình giảm tốc. Khi \(t\) tăng, quãng đường đi được giảm dần do vận tốc bị giảm.
- Thời gian dừng: Khi vận tốc của vật giảm xuống bằng 0, vật dừng lại. Thời gian để vật dừng lại hoàn toàn được tính bằng: \[ t_{\text{dừng}} = \frac{v_0}{a} \] Đây là khoảng thời gian mà vật mất để giảm hết vận tốc ban đầu \(v_0\) và đạt tới trạng thái nghỉ.
- Năng lượng và động lượng: Khi vật chuyển động chậm dần, năng lượng động học của nó cũng giảm dần: \[ E_{\text{k}} = \frac{1}{2} m v^2 \] Với \(v\) giảm, năng lượng động học cũng giảm, và khi \(v = 0\), vật không còn năng lượng động học.
Phân tích chuyển động thẳng chậm dần đều cho phép chúng ta hiểu rõ cách mà vận tốc, quãng đường, gia tốc và năng lượng thay đổi trong quá trình vật chuyển động. Những phương trình này là công cụ mạnh mẽ để giải quyết các bài toán liên quan đến chuyển động trong vật lý.

Những vấn đề thường gặp và cách khắc phục
Trong quá trình nghiên cứu và giải quyết các bài toán về chuyển động thẳng chậm dần đều, người học thường gặp phải một số vấn đề phổ biến. Dưới đây là những vấn đề thường gặp và cách khắc phục từng vấn đề một cách chi tiết.
1. Xác định sai gia tốc
Gia tốc trong chuyển động thẳng chậm dần đều luôn có giá trị âm, do đó nhiều người học thường mắc sai lầm khi sử dụng gia tốc dương trong các phương trình. Điều này dẫn đến việc tính toán sai vận tốc hoặc thời gian chuyển động.
- Cách khắc phục: Hãy luôn nhớ rằng gia tốc \(a < 0\) trong chuyển động chậm dần đều. Khi giải các bài toán, đảm bảo xác định đúng dấu của gia tốc trước khi thay vào các phương trình chuyển động.
2. Tính toán nhầm quãng đường
Một lỗi khác thường gặp là xác định sai quãng đường mà vật đã di chuyển. Điều này thường xảy ra khi người học quên rằng quãng đường không thể có giá trị âm, bất kể gia tốc có âm hay không.
- Cách khắc phục: Sử dụng công thức quãng đường \(s = v_0 t + \frac{1}{2} a t^2\) và kiểm tra lại xem kết quả của quãng đường có hợp lý hay không. Nếu kết quả ra âm, cần xem lại các bước tính toán.
3. Xác định sai vận tốc cuối cùng
Nhiều người gặp khó khăn trong việc tính vận tốc cuối cùng của vật khi chuyển động chậm dần đều. Một sai lầm phổ biến là không áp dụng đúng công thức hoặc nhầm lẫn giữa vận tốc cuối và vận tốc ban đầu.
- Cách khắc phục: Sử dụng chính xác công thức \(v = v_0 + a t\) để tính vận tốc tại mỗi thời điểm. Đảm bảo rằng gia tốc được thay thế với đúng dấu âm.
4. Xác định sai thời gian dừng
Thời gian vật dừng lại là một thông số quan trọng nhưng dễ bị nhầm lẫn khi không tính toán chính xác. Nhiều người không để ý rằng khi vật dừng lại, vận tốc bằng 0 và sử dụng sai công thức.
- Cách khắc phục: Khi giải bài toán, hãy luôn nhớ sử dụng điều kiện \(v = 0\) khi vật dừng lại và áp dụng công thức \(v = v_0 + a t\) để tính thời gian dừng.
5. Hiểu sai quỹ đạo chuyển động
Trong chuyển động thẳng chậm dần đều, một số học sinh nhầm lẫn rằng vật luôn đi theo đường thẳng hoặc không hiểu rõ quỹ đạo của chuyển động này.
- Cách khắc phục: Nhớ rằng trong chuyển động thẳng chậm dần đều, vật di chuyển theo quỹ đạo đường thẳng và vận tốc giảm dần cho đến khi bằng 0.
Kết luận
Để khắc phục những vấn đề trên, người học cần nắm rõ lý thuyết về chuyển động thẳng chậm dần đều, hiểu rõ các công thức và luôn kiểm tra lại kết quả tính toán. Khi áp dụng đúng các nguyên tắc này, việc giải các bài toán liên quan sẽ trở nên dễ dàng và chính xác hơn.
Tài liệu tham khảo và nguồn học liệu
Để hiểu rõ hơn về chuyển động thẳng chậm dần đều và áp dụng kiến thức này vào thực tế, dưới đây là một số tài liệu tham khảo và nguồn học liệu hữu ích:
Sách và tài liệu học tập
- Sách Vật lý lớp 10 - Cung cấp kiến thức cơ bản và các công thức liên quan đến chuyển động thẳng chậm dần đều.
- Giáo trình Vật lý đại cương - Bao gồm các bài giảng chi tiết về chuyển động thẳng chậm dần đều và các bài tập minh họa.
- Phương pháp giải bài tập Vật lý - Hướng dẫn cách giải các bài toán liên quan đến chuyển động thẳng chậm dần đều với ví dụ cụ thể.
Các nguồn tài nguyên trực tuyến
- Website VietJack - Cung cấp các bài viết và công thức về chuyển động thẳng chậm dần đều, bao gồm cả bài tập và đáp án.
- Website Khoahoc.vn - Cung cấp thông tin và giải thích chi tiết về các khái niệm và phương pháp liên quan đến chuyển động thẳng chậm dần đều.
- Youtube - Các video bài giảng và hướng dẫn giải bài tập về chuyển động thẳng chậm dần đều từ các giảng viên và chuyên gia.
Các khóa học trực tuyến
- Khóa học Vật lý trực tuyến - Các khóa học cung cấp bài giảng video và bài tập về chuyển động thẳng chậm dần đều.
- Chương trình luyện thi trực tuyến - Được thiết kế để giúp học sinh ôn tập và làm quen với các dạng bài tập về chuyển động thẳng chậm dần đều.