Vectơ Gia Tốc Trong Chuyển Động Thẳng Biến Đổi Đều: Định Nghĩa, Tính Chất và Ứng Dụng

Chuyển động thẳng biến đổi đều là một dạng chuyển động trong đó vận tốc của vật thay đổi đều đặn theo thời gian. Trong quá trình này, vectơ gia tốc đóng vai trò quan trọng trong việc xác định sự thay đổi vận tốc của vật.

1. Khái Niệm Vectơ Gia Tốc

Gia tốc \( \vec{a} \) là một đại lượng vectơ, được định nghĩa là thương số giữa độ biến thiên của vectơ vận tốc \( \Delta \vec{v} \) và khoảng thời gian \( \Delta t \) trong đó vận tốc biến thiên:

Trong chuyển động thẳng nhanh dần đều, vectơ gia tốc có phương và chiều trùng với phương và chiều của vectơ vận tốc, và có độ lớn không đổi.

2. Tính Chất Của Vectơ Gia Tốc

• Phương của vectơ gia tốc: Trùng với phương của vectơ vận tốc.
• Chiều của vectơ gia tốc: Nếu chuyển động nhanh dần đều, vectơ gia tốc cùng chiều với vectơ vận tốc; nếu chuyển động chậm dần đều, vectơ gia tốc ngược chiều với vectơ vận tốc.
• Độ lớn của vectơ gia tốc: Không đổi trong suốt quá trình chuyển động thẳng biến đổi đều.

3. Công Thức Tính Vận Tốc và Gia Tốc

Trong chuyển động thẳng nhanh dần đều, vận tốc \( v \) của vật tại một thời điểm bất kỳ có thể được tính bằng công thức:

Trong đó:

• \( v_0 \) là vận tốc ban đầu của vật.
• \( a \) là gia tốc không đổi.
• \( t \) là thời gian.

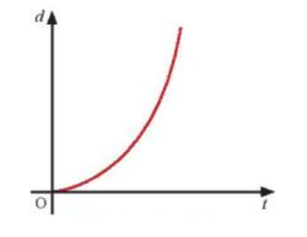
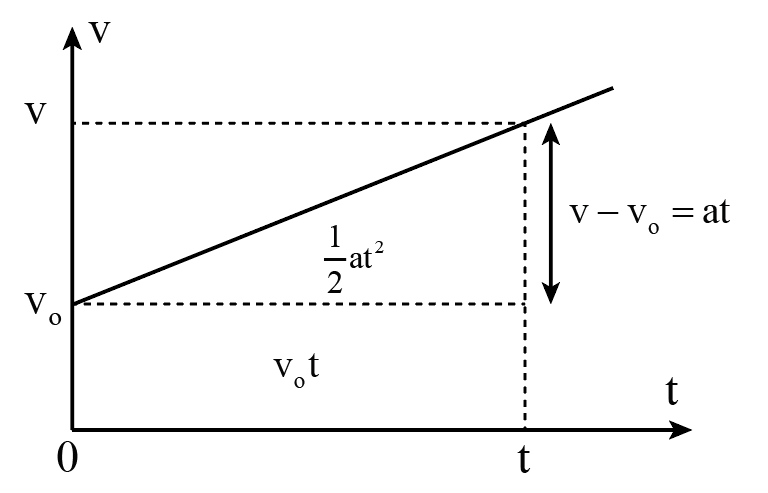
4. Đồ Thị Vận Tốc - Thời Gian

Đồ thị biểu diễn sự phụ thuộc của vận tốc theo thời gian là một đoạn thẳng, trong đó độ dốc của đoạn thẳng này chính là gia tốc \( a \).

5. Ứng Dụng Thực Tiễn

Vectơ gia tốc trong chuyển động thẳng biến đổi đều được ứng dụng rộng rãi trong các bài toán vật lý, đặc biệt là trong việc phân tích và dự đoán chuyển động của các vật thể trong cơ học cổ điển.

Việc nắm vững khái niệm và các công thức liên quan đến vectơ gia tốc giúp chúng ta hiểu rõ hơn về sự biến đổi của chuyển động trong cuộc sống hàng ngày, từ những ứng dụng đơn giản như chuyển động của xe cộ đến các nghiên cứu phức tạp trong khoa học và kỹ thuật.

Vectơ gia tốc là một đại lượng vật lý quan trọng, được sử dụng để mô tả sự biến thiên của vận tốc theo thời gian. Trong chuyển động thẳng biến đổi đều, vectơ gia tốc có một số đặc điểm quan trọng:

• Định nghĩa: Vectơ gia tốc (\(\overrightarrow{a}\)) là đại lượng vectơ biểu thị sự thay đổi của vận tốc (\(\overrightarrow{v}\)) theo thời gian (\(t\)). Công thức tổng quát của vectơ gia tốc là: \[ \overrightarrow{a} = \frac{\Delta \overrightarrow{v}}{\Delta t} \]
• Tính chất: Trong chuyển động thẳng biến đổi đều, vectơ gia tốc có các tính chất sau:
  1. Hướng: Vectơ gia tốc luôn cùng hướng hoặc ngược hướng với vectơ vận tốc, tùy thuộc vào chuyển động nhanh dần đều hay chậm dần đều.
  2. Độ lớn: Độ lớn của vectơ gia tốc là không đổi trong suốt quá trình chuyển động. Được tính bằng công thức: \[ a = \frac{\Delta v}{\Delta t} \]
• Chuyển động thẳng nhanh dần đều: Trong loại chuyển động này, vận tốc tăng đều theo thời gian, do đó vectơ gia tốc có cùng hướng với vectơ vận tốc.
• Chuyển động thẳng chậm dần đều: Ngược lại, trong chuyển động chậm dần đều, vận tốc giảm đều theo thời gian, dẫn đến vectơ gia tốc ngược hướng với vectơ vận tốc.

Tóm lại, vectơ gia tốc trong chuyển động thẳng biến đổi đều không chỉ đóng vai trò quan trọng trong việc xác định vận tốc của vật mà còn giúp hiểu rõ hơn về bản chất của chuyển động.

Chuyển động thẳng biến đổi đều là loại chuyển động trong đó vận tốc của vật thay đổi một cách đều đặn theo thời gian. Dựa trên đặc điểm của vectơ gia tốc, chuyển động thẳng biến đổi đều được phân thành hai loại chính:

• Chuyển động thẳng nhanh dần đều:
  1. Đặc điểm: Trong chuyển động này, vận tốc của vật tăng đều theo thời gian. Điều này có nghĩa là vectơ gia tốc (\(\overrightarrow{a}\)) và vectơ vận tốc (\(\overrightarrow{v}\)) có cùng hướng.
  2. Công thức: Vận tốc tại một thời điểm bất kỳ được tính bằng công thức: \[ v = v_0 + a t \] Trong đó:
     • \(v\): Vận tốc tại thời điểm \(t\)
     • \(v_0\): Vận tốc ban đầu
     • \(a\): Gia tốc không đổi
     • \(t\): Thời gian đã trôi qua
• Chuyển động thẳng chậm dần đều:
  1. Đặc điểm: Trong chuyển động này, vận tốc của vật giảm đều theo thời gian. Vectơ gia tốc (\(\overrightarrow{a}\)) có hướng ngược lại với vectơ vận tốc (\(\overrightarrow{v}\)).
  2. Công thức: Vận tốc tại một thời điểm bất kỳ trong chuyển động này được tính bằng công thức: \[ v = v_0 - a t \] Trong đó:
     • \(v\): Vận tốc tại thời điểm \(t\)
     • \(v_0\): Vận tốc ban đầu
     • \(a\): Gia tốc không đổi
     • \(t\): Thời gian đã trôi qua

Cả hai loại chuyển động thẳng biến đổi đều này đều tuân theo các nguyên tắc cơ bản của động học và được ứng dụng rộng rãi trong nhiều bài toán vật lý thực tiễn.

Trong chuyển động thẳng biến đổi đều, vectơ gia tốc là một yếu tố quan trọng xác định sự thay đổi vận tốc của vật theo thời gian. Dưới đây là các công thức liên quan đến vectơ gia tốc trong chuyển động thẳng biến đổi đều:

• Công thức tính gia tốc:

Gia tốc được tính bằng công thức:

\[
\vec{a} = \frac{\Delta \vec{v}}{\Delta t}
\]
Trong đó:




• \(\vec{a}\) là vectơ gia tốc (m/s²)


• \(\Delta \vec{v}\) là sự thay đổi vận tốc (m/s)


• \(\Delta t\) là khoảng thời gian tương ứng (s)




• Phương trình chuyển động:

Phương trình mô tả mối quan hệ giữa vị trí, vận tốc và gia tốc của vật trong chuyển động thẳng biến đổi đều:

\[
v = v_0 + at
\]
\[
x = x_0 + v_0t + \frac{1}{2}at^2
\]
\[
v^2 = v_0^2 + 2a(x - x_0)
\]
Trong đó:




• \(v\) là vận tốc tại thời điểm \(t\) (m/s)


• \(v_0\) là vận tốc ban đầu (m/s)


• \(x\) là vị trí tại thời điểm \(t\) (m)


• \(x_0\) là vị trí ban đầu (m)


• \(a\) là gia tốc (m/s²)


• \(t\) là thời gian (s)




• Mối quan hệ giữa gia tốc và độ dốc của đồ thị vận tốc:

Trong đồ thị vận tốc theo thời gian, độ dốc của đường thẳng biểu thị chính là gia tốc. Nếu độ dốc dương, chuyển động là nhanh dần đều; nếu độ dốc âm, chuyển động là chậm dần đều.

Vectơ gia tốc là một khái niệm quan trọng trong vật lý học, đặc biệt là trong việc phân tích các loại chuyển động. Những ứng dụng của vectơ gia tốc không chỉ giới hạn trong các bài toán lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật. Dưới đây là một số ứng dụng điển hình của vectơ gia tốc:

• Thiết kế và vận hành phương tiện giao thông:

  Vectơ gia tốc đóng vai trò quan trọng trong việc thiết kế hệ thống phanh và tăng tốc của các phương tiện giao thông như ô tô, xe máy, và tàu hỏa. Việc tính toán chính xác gia tốc giúp cải thiện hiệu suất và độ an toàn của phương tiện khi di chuyển ở các tốc độ khác nhau.

• Điều khiển robot và máy móc:

  Trong lĩnh vực robot và tự động hóa, vectơ gia tốc được sử dụng để điều khiển chuyển động của các cánh tay robot hoặc các thiết bị tự động. Các cảm biến gia tốc được tích hợp để đảm bảo các chuyển động diễn ra mượt mà và chính xác, tránh các va chạm và hỏng hóc không mong muốn.

• Công nghệ hàng không và vũ trụ:

  Vectơ gia tốc được áp dụng trong việc điều hướng và kiểm soát tàu vũ trụ, máy bay, và tên lửa. Khả năng tính toán và kiểm soát vectơ gia tốc giúp đảm bảo các thiết bị này di chuyển đúng quỹ đạo, thực hiện các nhiệm vụ như tiếp đất, quay trở về, và giữ ổn định trong không gian.

• Phân tích các bài toán trong xây dựng:

  Trong xây dựng, vectơ gia tốc được sử dụng để phân tích sức chịu đựng của các công trình khi gặp phải tác động của lực, chẳng hạn như trong các trận động đất hoặc gió bão. Các kỹ sư sử dụng các mô hình mô phỏng để tính toán và thiết kế các công trình chịu được các lực tác động bất thường này.

• Nghiên cứu khoa học:

  Vectơ gia tốc là công cụ không thể thiếu trong nghiên cứu khoa học, từ việc phân tích chuyển động của các hạt trong vật lý hạt nhân đến việc nghiên cứu sự chuyển động của các thiên thể trong thiên văn học.

Như vậy, vectơ gia tốc không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn, đóng góp vào sự phát triển của khoa học kỹ thuật và đời sống hàng ngày.

• 1. Vectơ gia tốc trong chuyển động thẳng biến đổi đều là gì?

  Vectơ gia tốc là đại lượng vectơ biểu thị sự thay đổi của vectơ vận tốc theo thời gian trong chuyển động thẳng biến đổi đều. Nó thể hiện cả về độ lớn lẫn hướng của sự thay đổi vận tốc.

• 2. Vectơ gia tốc có luôn cùng hướng với vectơ vận tốc không?

  Không, vectơ gia tốc không nhất thiết phải cùng hướng với vectơ vận tốc. Trong trường hợp gia tốc âm (chuyển động chậm dần đều), vectơ gia tốc sẽ ngược hướng với vectơ vận tốc.

• 3. Công thức tính vectơ gia tốc trong chuyển động thẳng biến đổi đều là gì?

  Trong chuyển động thẳng biến đổi đều, gia tốc được tính bằng công thức: \[ a = \frac{\Delta v}{\Delta t} \], trong đó \( \Delta v \) là sự thay đổi vận tốc và \( \Delta t \) là khoảng thời gian thay đổi.

• 4. Vectơ gia tốc ảnh hưởng thế nào đến chuyển động của vật?

  Vectơ gia tốc quyết định sự thay đổi vận tốc của vật theo thời gian. Nếu gia tốc dương, vận tốc tăng dần, nếu gia tốc âm, vận tốc giảm dần.

• 5. Các ứng dụng thực tiễn của vectơ gia tốc là gì?

  Vectơ gia tốc có nhiều ứng dụng trong đời sống, như thiết kế phanh xe, điều khiển robot, nghiên cứu chuyển động thiên thể, và nhiều lĩnh vực khác.