Chủ đề một vật chuyển động thẳng biến đổi đều thì: Một vật chuyển động thẳng biến đổi đều thì là chủ đề quan trọng trong vật lý học. Bài viết này sẽ giúp bạn hiểu rõ về khái niệm, công thức tính toán và các ứng dụng thực tế của chuyển động thẳng biến đổi đều, từ đó áp dụng kiến thức vào các bài toán và cuộc sống hàng ngày.
Mục lục
- Một Vật Chuyển Động Thẳng Biến Đổi Đều Thì
- 1. Khái Niệm Chuyển Động Thẳng Biến Đổi Đều
- 2. Các Công Thức Liên Quan Đến Chuyển Động Thẳng Biến Đổi Đều
- 3. Các Bài Tập Về Chuyển Động Thẳng Biến Đổi Đều
- 4. Ứng Dụng Thực Tế Của Chuyển Động Thẳng Biến Đổi Đều
- 5. Tài Liệu Tham Khảo Về Chuyển Động Thẳng Biến Đổi Đều
Một Vật Chuyển Động Thẳng Biến Đổi Đều Thì
Trong vật lý học, chuyển động thẳng biến đổi đều là một khái niệm quan trọng, đặc biệt trong việc nghiên cứu các hiện tượng chuyển động. Dưới đây là các thông tin chi tiết về chuyển động thẳng biến đổi đều và cách tính toán.
1. Định Nghĩa
Chuyển động thẳng biến đổi đều là chuyển động có vận tốc thay đổi đều theo thời gian. Trong đó, gia tốc của vật là một đại lượng không đổi, tức là:
\[ a = \frac{\Delta v}{\Delta t} = const \]
2. Công Thức Tính Toán
- Vận tốc tức thời của vật tại thời điểm \( t \):
- Quãng đường vật đi được sau thời gian \( t \):
- Vận tốc cuối cùng liên quan đến quãng đường và gia tốc:
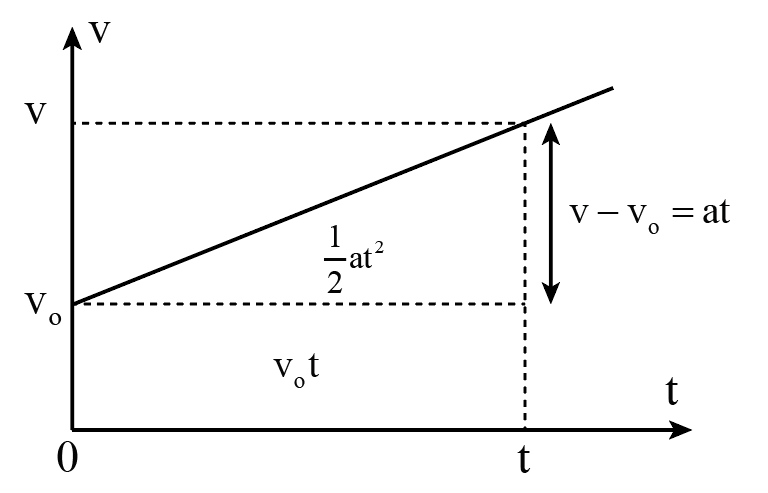
\[ v = v_0 + a t \]
\[ s = v_0 t + \frac{1}{2} a t^2 \]
\[ v^2 = v_0^2 + 2 a s \]
3. Ví Dụ Minh Họa
Giả sử một vật có vận tốc ban đầu \( v_0 = 5 \, \text{m/s} \) và gia tốc không đổi \( a = 2 \, \text{m/s}^2 \). Sau \( 3 \, \text{s} \), vận tốc tức thời của vật là:
\[ v = 5 + 2 \times 3 = 11 \, \text{m/s} \]
Quãng đường mà vật đi được sau \( 3 \, \text{s} \) là:
\[ s = 5 \times 3 + \frac{1}{2} \times 2 \times 3^2 = 15 + 9 = 24 \, \text{m} \]
4. Kết Luận
Chuyển động thẳng biến đổi đều là một loại chuyển động cơ bản và thường gặp trong các bài toán vật lý. Việc nắm vững công thức và cách tính toán sẽ giúp hiểu rõ hơn về cách mà các đối tượng di chuyển trong thực tế.

.png)
1. Khái Niệm Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều là một loại chuyển động quan trọng trong vật lý học, trong đó vận tốc của vật thay đổi đều theo thời gian. Điều này có nghĩa là vật di chuyển theo một đường thẳng với gia tốc không đổi.
Để hiểu rõ hơn, chúng ta có thể định nghĩa chuyển động thẳng biến đổi đều như sau:
- Vận tốc của vật thay đổi đều theo thời gian, tức là:
- Gia tốc là đại lượng không đổi, và vận tốc của vật thay đổi tuyến tính theo thời gian:
\[ a = const \]
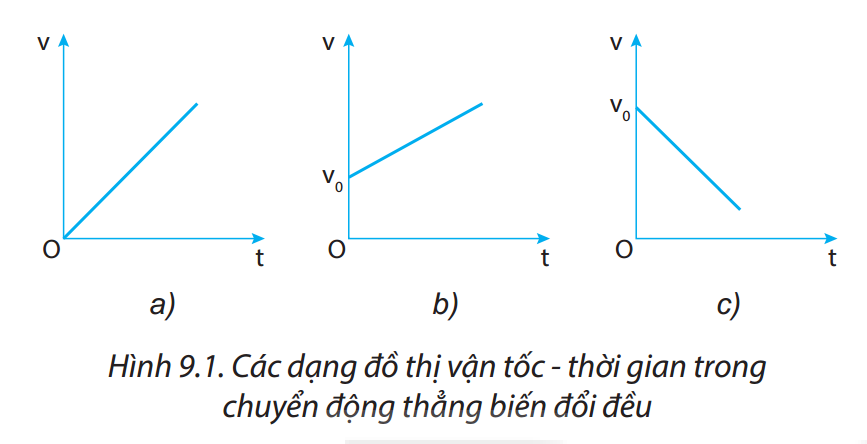
\[ v = v_0 + a t \]
Trong chuyển động thẳng biến đổi đều, quãng đường mà vật di chuyển được có thể tính bằng công thức:
\[ s = v_0 t + \frac{1}{2} a t^2 \]
Ở đây:
- \(v_0\) là vận tốc ban đầu của vật.
- \(a\) là gia tốc không đổi của vật.
- \(t\) là thời gian mà vật di chuyển.
- \(s\) là quãng đường mà vật đã di chuyển.
Ví dụ, nếu một vật có vận tốc ban đầu là \(v_0 = 0\) và gia tốc không đổi \(a = 2 \, \text{m/s}^2\), thì sau 5 giây, vận tốc của vật sẽ là:
\[ v = 0 + 2 \times 5 = 10 \, \text{m/s} \]
Quãng đường mà vật đi được trong khoảng thời gian này là:
\[ s = 0 \times 5 + \frac{1}{2} \times 2 \times 5^2 = 25 \, \text{m} \]
Chuyển động thẳng biến đổi đều là nền tảng để giải quyết nhiều bài toán khác trong vật lý, giúp chúng ta hiểu rõ hơn về cách các đối tượng di chuyển trong thực tế.
2. Các Công Thức Liên Quan Đến Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều là chuyển động có gia tốc không đổi theo thời gian. Các công thức cơ bản liên quan đến chuyển động này bao gồm:
2.1. Công Thức Tính Vận Tốc
Vận tốc tức thời \(v_t\) của một vật tại thời điểm \(t\) được tính theo công thức:
\[v_t = v_0 + a \cdot t\]
Trong đó:
- \(v_t\): Vận tốc tại thời điểm \(t\) (m/s)
- \(v_0\): Vận tốc ban đầu (m/s)
- \(a\): Gia tốc (m/s2)
- \(t\): Thời gian (s)
2.2. Công Thức Tính Quãng Đường
Quãng đường \(s\) mà vật di chuyển trong khoảng thời gian \(t\) được tính theo công thức:
\[s = v_0 \cdot t + \dfrac{1}{2} \cdot a \cdot t^2\]
Trong đó:
- \(s\): Quãng đường (m)
- \(v_0\): Vận tốc ban đầu (m/s)
- \(a\): Gia tốc (m/s2)
- \(t\): Thời gian (s)
2.3. Công Thức Liên Hệ Giữa Vận Tốc, Gia Tốc và Quãng Đường
Công thức liên hệ giữa vận tốc cuối cùng \(v_t\), vận tốc ban đầu \(v_0\), gia tốc \(a\), và quãng đường \(s\) là:
\[v_t^2 = v_0^2 + 2 \cdot a \cdot s\]
Trong đó:
- \(v_t\): Vận tốc tại thời điểm \(t\) (m/s)
- \(v_0\): Vận tốc ban đầu (m/s)
- \(a\): Gia tốc (m/s2)
- \(s\): Quãng đường (m)

3. Các Bài Tập Về Chuyển Động Thẳng Biến Đổi Đều
Dưới đây là một số bài tập cơ bản và nâng cao về chuyển động thẳng biến đổi đều. Các bài tập này sẽ giúp bạn nắm vững các khái niệm và công thức liên quan.
3.1. Bài Tập Tính Vận Tốc
-
Bài tập 1: Một vật bắt đầu chuyển động với vận tốc ban đầu \(v_0 = 0\). Sau 5 giây, vận tốc của vật đạt \(v = 10 \, \text{m/s}\). Tính gia tốc \(a\) của vật.
Lời giải:
Áp dụng công thức: \(v = v_0 + at\), ta có:
\[ 10 = 0 + a \times 5 \]=> \(a = 2 \, \text{m/s}^2\)
-
Bài tập 2: Một vật chuyển động thẳng biến đổi đều với vận tốc ban đầu \(v_0 = 5 \, \text{m/s}\). Sau 4 giây, vận tốc của vật là \(v = 25 \, \text{m/s}\). Tính gia tốc của vật.
Lời giải:
Áp dụng công thức: \(v = v_0 + at\), ta có:
\[ 25 = 5 + a \times 4 \]=> \(a = 5 \, \text{m/s}^2\)
3.2. Bài Tập Tính Quãng Đường
-
Bài tập 3: Một vật bắt đầu chuyển động với vận tốc ban đầu \(v_0 = 0\) và gia tốc \(a = 3 \, \text{m/s}^2\). Tính quãng đường \(s\) vật đi được trong 5 giây đầu tiên.
Lời giải:
Áp dụng công thức: \(s = v_0t + \frac{1}{2}at^2\), ta có:
\[ s = 0 \times 5 + \frac{1}{2} \times 3 \times 5^2 = 37.5 \, \text{m} \] -
Bài tập 4: Một xe đang chạy với vận tốc \(v_0 = 20 \, \text{m/s}\) thì bắt đầu giảm tốc độ với gia tốc \(a = -2 \, \text{m/s}^2\). Tính quãng đường xe đi được cho đến khi dừng hẳn.
Lời giải:
Áp dụng công thức: \(v^2 = v_0^2 + 2as\), với \(v = 0\), ta có:
\[ 0 = 20^2 + 2(-2)s \]=> \(s = 100 \, \text{m}\)
3.3. Bài Tập Tính Gia Tốc
-
Bài tập 5: Một xe máy bắt đầu chuyển động từ trạng thái nghỉ với gia tốc không đổi. Sau khi đi được quãng đường \(s = 100 \, \text{m}\), vận tốc của xe đạt \(v = 20 \, \text{m/s}\). Tính gia tốc \(a\) của xe.
Lời giải:
Áp dụng công thức: \(v^2 = v_0^2 + 2as\), với \(v_0 = 0\), ta có:
\[ 20^2 = 0 + 2a \times 100 \]=> \(a = 2 \, \text{m/s}^2\)
-
Bài tập 6: Một đoàn tàu đang chạy với vận tốc \(v_0 = 36 \, \text{km/h}\) thì hãm phanh. Sau 5 giây, tàu dừng hẳn. Tính gia tốc và quãng đường tàu đi được trong thời gian hãm phanh.
Lời giải:
Đổi \(v_0 = 36 \, \text{km/h} = 10 \, \text{m/s}\). Áp dụng công thức: \(v = v_0 + at\), với \(v = 0\), ta có:
\[ 0 = 10 + a \times 5 \]=> \(a = -2 \, \text{m/s}^2\)
Quãng đường tàu đi được:
\[ s = v_0t + \frac{1}{2}at^2 = 10 \times 5 + \frac{1}{2}(-2) \times 5^2 = 25 \, \text{m} \]
4. Ứng Dụng Thực Tế Của Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều có nhiều ứng dụng thực tế quan trọng trong cuộc sống, đặc biệt là trong các lĩnh vực như giao thông, thiết kế cơ khí và các nghiên cứu khoa học.
4.1. Ứng Dụng Trong Giao Thông
Kiểm soát tốc độ: Việc hiểu rõ quy luật chuyển động thẳng biến đổi đều giúp các kỹ sư giao thông thiết kế và kiểm soát tốc độ của các phương tiện. Ví dụ, khi một xe ô tô tăng tốc từ trạng thái nghỉ đến một vận tốc nhất định, quy luật này giúp tính toán thời gian và khoảng cách cần thiết để đạt được tốc độ mong muốn.
Dừng khẩn cấp: Trong tình huống dừng khẩn cấp, các phương tiện sẽ sử dụng nguyên lý của chuyển động thẳng biến đổi đều để tính toán khoảng cách phanh cần thiết, nhằm đảm bảo an toàn cho người tham gia giao thông.
4.2. Ứng Dụng Trong Thiết Kế Cơ Khí
Thiết kế hệ thống truyền động: Trong các hệ thống cơ khí như băng chuyền, thang máy, việc tính toán gia tốc và vận tốc dựa trên chuyển động thẳng biến đổi đều là rất quan trọng để đảm bảo thiết bị hoạt động ổn định và hiệu quả.
Tối ưu hóa hiệu suất máy móc: Các kỹ sư có thể sử dụng công thức của chuyển động thẳng biến đổi đều để tối ưu hóa hiệu suất của các thiết bị cơ khí, đảm bảo chúng hoạt động với tốc độ phù hợp mà không gây mài mòn quá mức.
Những ứng dụng trên cho thấy tầm quan trọng của việc nắm vững kiến thức về chuyển động thẳng biến đổi đều trong việc giải quyết các vấn đề thực tiễn và nâng cao hiệu suất trong các lĩnh vực kỹ thuật và giao thông.

5. Tài Liệu Tham Khảo Về Chuyển Động Thẳng Biến Đổi Đều
Để hiểu rõ hơn về chuyển động thẳng biến đổi đều, dưới đây là một số tài liệu tham khảo hữu ích giúp bạn củng cố kiến thức và làm bài tập hiệu quả:
-
Giáo trình Vật Lý 10: Đây là nguồn tài liệu cơ bản, cung cấp kiến thức nền tảng về chuyển động thẳng biến đổi đều, bao gồm các công thức quan trọng như:
- Phương trình tọa độ: \( x = x_0 + v_0(t - t_0) + \frac{1}{2}a(t - t_0)^2 \)
- Phương trình vận tốc: \( v = v_0 + a(t - t_0) \)
- Hệ thức độc lập thời gian: \( v^2 - v_0^2 = 2a\Delta x \)
- Bài giảng online và video học tập: Các bài giảng trực tuyến và video học tập trên các nền tảng giáo dục như YouTube, Marathon Education, hay các trang web học tập khác giúp bạn tiếp cận kiến thức một cách trực quan và sinh động. Ví dụ, các video giải thích đồ thị vận tốc-thời gian, hay cách áp dụng công thức vào các bài toán thực tế sẽ giúp bạn nắm vững kiến thức hơn.
- Ứng dụng giải bài tập: Các ứng dụng như Wolfram Alpha, GeoGebra hay các công cụ trực tuyến khác giúp bạn giải nhanh các bài toán về chuyển động thẳng biến đổi đều, đồng thời cung cấp lời giải chi tiết từng bước.
- Sách tham khảo nâng cao: Nếu bạn muốn đi sâu hơn vào lĩnh vực này, hãy tìm đọc các sách nâng cao như "Vật Lý Đại Cương" của các tác giả nổi tiếng. Những cuốn sách này không chỉ cung cấp kiến thức mở rộng mà còn mang lại các bài tập thực hành đa dạng và phong phú.
Bằng cách kết hợp các tài liệu trên, bạn sẽ có thể nắm vững lý thuyết và áp dụng hiệu quả vào việc giải các bài tập về chuyển động thẳng biến đổi đều.