Các Dạng Bài Tập Chuyển Động Thẳng Biến Đổi Đều: Hướng Dẫn Chi Tiết Và Bài Tập Thực Hành

Chuyển động thẳng biến đổi đều là dạng chuyển động trong đó gia tốc của vật là không đổi. Dưới đây là các dạng bài tập phổ biến liên quan đến chủ đề này, kèm theo phương pháp giải và công thức toán học liên quan.

Dạng 1: Tính vận tốc trong chuyển động thẳng biến đổi đều

Sử dụng công thức:

\[v = v_0 + at\]

• \(v\): Vận tốc tại thời điểm \(t\)
• \(v_0\): Vận tốc ban đầu
• \(a\): Gia tốc của chuyển động
• \(t\): Thời gian

Dạng 2: Tính quãng đường đi được

Quãng đường vật đi được trong chuyển động thẳng biến đổi đều được tính bằng công thức:

\[s = v_0t + \frac{1}{2}at^2\]

• \(s\): Quãng đường vật đã di chuyển
• Các ký hiệu khác như trong công thức vận tốc

Dạng 3: Viết phương trình chuyển động

Phương trình chuyển động thẳng biến đổi đều có dạng:

\[x = x_0 + v_0t + \frac{1}{2}at^2\]

• \(x\): Vị trí tại thời điểm \(t\)
• \(x_0\): Vị trí ban đầu
• Các ký hiệu khác như trên

Dạng 4: Tính vận tốc độc lập thời gian

Trong trường hợp không biết thời gian, vận tốc có thể được tính theo công thức:

\[v^2 = v_0^2 + 2a(x - x_0)\]

Trong đó:

• \(x - x_0\): Quãng đường đã đi

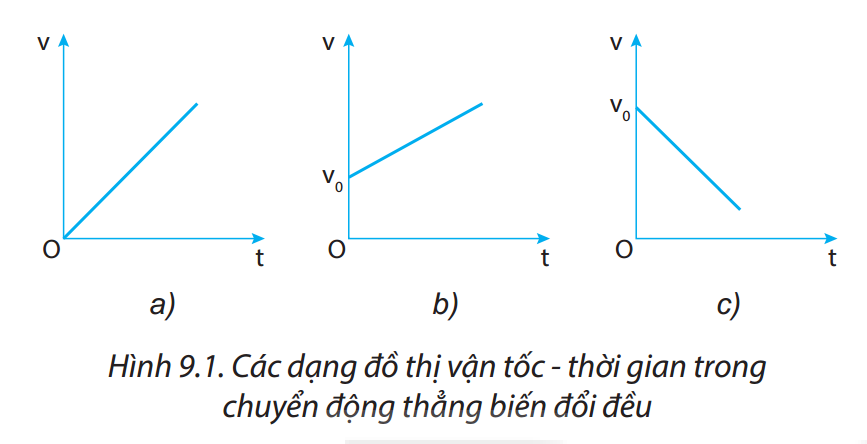
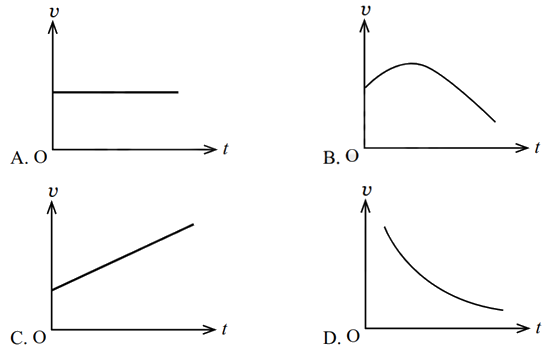
Dạng 5: Đồ thị của chuyển động thẳng biến đổi đều

Các đồ thị trong bài tập chuyển động thẳng biến đổi đều thường bao gồm:

• Đồ thị vận tốc – thời gian
• Đồ thị gia tốc – thời gian
• Đồ thị quãng đường – thời gian

Việc phân tích và vẽ đồ thị giúp làm rõ mối quan hệ giữa các đại lượng trong chuyển động.

Dạng 6: Bài tập tổng hợp

Các bài tập tổng hợp yêu cầu kết hợp nhiều công thức để tính toán các đại lượng như vận tốc, quãng đường, và gia tốc từ các dữ kiện khác nhau.

Các dạng bài tập chuyển động thẳng biến đổi đều đóng vai trò quan trọng trong chương trình học Vật lý lớp 10. Học sinh cần nắm vững công thức và phương pháp giải để giải quyết tốt các bài tập liên quan.

Các dạng bài tập chuyển động thẳng biến đổi đều đóng vai trò quan trọng trong chương trình học Vật lý lớp 10. Học sinh cần nắm vững công thức và phương pháp giải để giải quyết tốt các bài tập liên quan.

Chuyển động thẳng biến đổi đều là loại chuyển động mà vận tốc của vật thay đổi đều đặn theo thời gian. Điều này có nghĩa là gia tốc của vật luôn không đổi và có thể dương (chuyển động nhanh dần đều) hoặc âm (chuyển động chậm dần đều).

Trong chuyển động thẳng biến đổi đều, có hai trường hợp chính:

• Chuyển động thẳng nhanh dần đều: Vận tốc của vật tăng đều theo thời gian với gia tốc \( a > 0 \).
• Chuyển động thẳng chậm dần đều: Vận tốc của vật giảm đều theo thời gian với gia tốc \( a < 0 \).

Công thức cơ bản của chuyển động thẳng biến đổi đều là:

• Phương trình vận tốc: \( v = v_0 + at \), trong đó:
  • \( v_0 \) là vận tốc ban đầu
  • \( a \) là gia tốc
  • \( t \) là thời gian
• Phương trình quãng đường: \( s = v_0t + \frac{1}{2}at^2 \)
• Công thức liên hệ giữa vận tốc và quãng đường: \( v^2 = v_0^2 + 2as \)

Trong đó:

• \( v \): Vận tốc của vật sau khoảng thời gian \( t \)
• \( v_0 \): Vận tốc ban đầu của vật
• \( a \): Gia tốc (có thể âm hoặc dương)
• \( t \): Thời gian chuyển động
• \( s \): Quãng đường đi được

Một ví dụ thực tế về chuyển động thẳng biến đổi đều là khi một chiếc xe ô tô bắt đầu chuyển động nhanh dần đều từ trạng thái đứng yên. Khi đó, vận tốc của xe sẽ tăng lên đều đặn cho đến khi đạt đến một giá trị nhất định.

Trong chuyển động thẳng biến đổi đều, các đại lượng cơ bản bao gồm:

• Vận tốc tức thời \(v\): Đây là đại lượng đo sự thay đổi vị trí của vật theo thời gian. Vận tốc tức thời tại thời điểm \(t\) được tính bằng công thức: \[ v = v_0 + a \cdot t \] Trong đó:
  • \(v_0\): Vận tốc ban đầu (m/s)
  • \(a\): Gia tốc (m/s²)
  • \(t\): Thời gian (s)
• Gia tốc \(a\): Là đại lượng đặc trưng cho sự thay đổi vận tốc của vật trong một khoảng thời gian. Công thức tính gia tốc là: \[ a = \frac{v - v_0}{t} \] Trong đó:
  • \(v\): Vận tốc tại thời điểm t (m/s)
  • \(v_0\): Vận tốc ban đầu (m/s)
  • \(t\): Thời gian (s)
• Quãng đường \(s\): Là tổng độ dài đường đi của vật trong một khoảng thời gian. Đối với chuyển động thẳng biến đổi đều, quãng đường được tính bằng công thức: \[ s = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 \] Trong đó:
  • \(s\): Quãng đường (m)
  • \(v_0\): Vận tốc ban đầu (m/s)
  • \(a\): Gia tốc (m/s²)
  • \(t\): Thời gian (s)
• Phương trình chuyển động: Phương trình mô tả vị trí của vật theo thời gian là: \[ x = x_0 + v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 \] Trong đó:
  • \(x\): Vị trí của vật tại thời điểm \(t\) (m)
  • \(x_0\): Vị trí ban đầu (m)
  • \(v_0\): Vận tốc ban đầu (m/s)
  • \(a\): Gia tốc (m/s²)
  • \(t\): Thời gian (s)

Trong chuyển động thẳng biến đổi đều, có nhiều dạng bài tập phổ biến nhằm giúp học sinh hiểu và áp dụng các công thức vật lý để giải quyết các vấn đề liên quan. Các dạng bài tập này thường xoay quanh việc tính toán vận tốc, quãng đường, và gia tốc của vật thể.

• Dạng 1: Tính gia tốc và vận tốc tức thời

  Ví dụ: Một ô tô đang chuyển động với vận tốc ban đầu là \(v_0 = 20 \, km/h\) và gia tốc \(a = 2 \, m/s^2\). Hãy tính vận tốc của xe sau \(t = 5 \, s\).

  Công thức áp dụng: \[ v = v_0 + a \cdot t \]

• Dạng 2: Tính quãng đường đi được

  Ví dụ: Một vật bắt đầu chuyển động từ trạng thái nghỉ với gia tốc không đổi \(a = 1.5 \, m/s^2\). Tính quãng đường đi được sau 10 giây.

  Công thức áp dụng: \[ S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 \]

• Dạng 3: Bài toán về phương trình chuyển động

  Ví dụ: Viết phương trình chuyển động của một vật chuyển động nhanh dần đều với vận tốc ban đầu \(v_0 = 5 \, m/s\) và gia tốc \(a = 0.8 \, m/s^2\).

  Phương trình: \[ x = x_0 + v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 \]

Các bài tập này yêu cầu sử dụng các phương trình cơ bản của chuyển động thẳng biến đổi đều như vận tốc, quãng đường, và gia tốc để tìm kiếm lời giải.

Dưới đây là các bài tập chi tiết giúp bạn thực hành và củng cố kiến thức về chuyển động thẳng biến đổi đều. Mỗi bài tập đi kèm hướng dẫn và lời giải cụ thể, giúp bạn hiểu rõ hơn cách áp dụng các công thức vật lý đã học.

• Bài tập 1: Tính quãng đường và vận tốc
  1. Đề bài: Một vật bắt đầu chuyển động từ trạng thái nghỉ, với gia tốc không đổi \(a = 2 \, m/s^2\). Tính quãng đường vật đi được sau \(t = 8 \, s\).
  2. Hướng dẫn: Sử dụng công thức \[S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2\]
  3. Lời giải: Quãng đường đi được là \[S = 0 + \frac{1}{2} \cdot 2 \cdot 8^2 = 64 \, m\]
• Bài tập 2: Vận tốc tức thời của vật
  1. Đề bài: Một xe ô tô chuyển động với vận tốc ban đầu \(v_0 = 10 \, m/s\) và gia tốc \(a = 1.5 \, m/s^2\). Tính vận tốc của xe sau \(t = 6 \, s\).
  2. Hướng dẫn: Áp dụng công thức tính vận tốc \[v = v_0 + a \cdot t\]
  3. Lời giải: Vận tốc sau \(t = 6 \, s\) là \[v = 10 + 1.5 \cdot 6 = 19 \, m/s\]
• Bài tập 3: Phương trình chuyển động
  1. Đề bài: Một vật chuyển động nhanh dần đều với gia tốc \(a = 0.5 \, m/s^2\), vận tốc ban đầu \(v_0 = 5 \, m/s\). Hãy viết phương trình chuyển động của vật sau \(t = 4 \, s\).
  2. Hướng dẫn: Sử dụng phương trình chuyển động \[x = x_0 + v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2\]
  3. Lời giải: Phương trình chuyển động của vật là \[x = 0 + 5 \cdot 4 + \frac{1}{2} \cdot 0.5 \cdot 4^2 = 20 + 4 = 24 \, m\]

Thực hành các dạng bài tập này sẽ giúp bạn làm quen với cách áp dụng lý thuyết và công thức vào thực tế, từ đó nắm vững kiến thức về chuyển động thẳng biến đổi đều.

Các công thức cơ bản trong chuyển động thẳng biến đổi đều giúp xác định các đại lượng như vận tốc, quãng đường và gia tốc của vật chuyển động. Dưới đây là các công thức quan trọng cần ghi nhớ:

• Công thức tính vận tốc: \[v = v_0 + a \cdot t\]
  • \(v\) là vận tốc tức thời tại thời điểm \(t\)
  • \(v_0\) là vận tốc ban đầu
  • \(a\) là gia tốc của vật
  • \(t\) là thời gian
• Công thức tính quãng đường: \[S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2\]
  • \(S\) là quãng đường vật đã đi
  • \(v_0\) là vận tốc ban đầu
  • \(a\) là gia tốc của vật
  • \(t\) là thời gian chuyển động
• Công thức liên hệ giữa vận tốc và quãng đường: \[v^2 = v_0^2 + 2aS\]
  • \(v\) là vận tốc tại thời điểm cần tính
  • \(v_0\) là vận tốc ban đầu
  • \(a\) là gia tốc của vật
  • \(S\) là quãng đường vật đi được

Các công thức này giúp giải quyết hầu hết các bài toán liên quan đến chuyển động thẳng biến đổi đều, cung cấp cơ sở lý thuyết và thực tiễn cho các bài tập phức tạp hơn.

Chuyển động thẳng biến đổi đều là một trong những dạng chuyển động cơ bản và quan trọng trong vật lý, có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và kỹ thuật. Việc nắm vững kiến thức về chuyển động này không chỉ giúp học sinh hiểu sâu hơn về các khái niệm vật lý mà còn có thể áp dụng trong thực tế.

6.1. Các Đặc Điểm Quan Trọng Của Chuyển Động Thẳng Biến Đổi Đều

• Tính đều đặn: Trong chuyển động thẳng biến đổi đều, gia tốc của vật không đổi, nghĩa là vận tốc thay đổi một cách đều đặn theo thời gian.
• Phương trình chuyển động: Có thể xác định vị trí, vận tốc, và gia tốc của vật tại bất kỳ thời điểm nào thông qua các phương trình liên quan.
• Ứng dụng thực tiễn: Chuyển động thẳng biến đổi đều xuất hiện trong nhiều trường hợp thực tế, chẳng hạn như sự giảm tốc của xe ô tô khi phanh hoặc sự tăng tốc của vật rơi tự do.

6.2. Ứng Dụng Của Chuyển Động Thẳng Trong Cuộc Sống

• Trong giao thông: Hiểu biết về chuyển động thẳng biến đổi đều giúp tính toán quãng đường, vận tốc và thời gian cần thiết trong các tình huống giao thông như phanh khẩn cấp, tăng tốc.
• Trong kỹ thuật và công nghệ: Chuyển động của các máy móc, robot, và các thiết bị tự động đều được thiết kế dựa trên nguyên lý của chuyển động thẳng biến đổi đều.
• Trong giáo dục: Học sinh nắm vững kiến thức này sẽ có nền tảng tốt để tiếp cận các dạng chuyển động phức tạp hơn trong tương lai.

Tóm lại, chuyển động thẳng biến đổi đều không chỉ là một khái niệm lý thuyết mà còn có những ứng dụng thực tiễn quan trọng. Việc hiểu và áp dụng chính xác các công thức và quy luật của chuyển động này sẽ giúp chúng ta giải quyết được nhiều bài toán trong thực tế, từ đó cải thiện hiệu quả công việc và nâng cao chất lượng cuộc sống.