Chủ đề đồ thị của chuyển động thẳng biến đổi đều: Khám phá chi tiết về đồ thị của chuyển động thẳng biến đổi đều, từ khái niệm cơ bản đến các ứng dụng thực tiễn trong cuộc sống. Bài viết này sẽ cung cấp cho bạn cái nhìn toàn diện về cách phân tích đồ thị và hiểu rõ hơn về các hiện tượng vật lý liên quan.
Mục lục
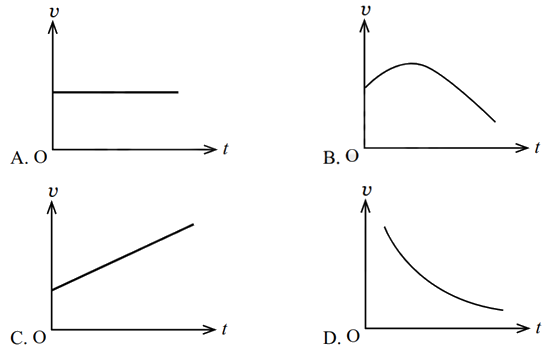
Đồ Thị Của Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều là một trong những chủ đề quan trọng trong môn Vật lý lớp 10. Nó liên quan đến sự thay đổi vận tốc theo thời gian của một vật thể chuyển động trên quỹ đạo thẳng. Có hai loại chuyển động chính trong chuyển động thẳng biến đổi đều: chuyển động nhanh dần đều và chuyển động chậm dần đều.
Các Đại Lượng Trong Chuyển Động Thẳng Biến Đổi Đều
- Gia tốc (\(\vec{a}\)): Đây là đại lượng đặc trưng cho tốc độ thay đổi của vận tốc. Gia tốc được tính theo công thức: \[ \vec{a} = \frac{\vec{v} - \vec{v_0}}{\Delta t} \]
- Phương trình tọa độ (\(x\)): Tọa độ của vật thể theo thời gian được mô tả bởi: \[ x = x_0 + v_0(t - t_0) + \frac{1}{2}a(t - t_0)^2 \]
- Phương trình vận tốc (\(v\)): Vận tốc của vật thể theo thời gian được xác định như sau: \[ v = v_0 + a(t - t_0) \]
- Hệ thức độc lập thời gian: Liên hệ giữa vận tốc và quãng đường mà không cần thời gian: \[ v^2 - v_0^2 = 2a\Delta x \]
Đồ Thị Của Chuyển Động Thẳng Biến Đổi Đều
Đồ thị của chuyển động thẳng biến đổi đều có thể được biểu diễn dưới hai dạng chính:
- Đồ thị vận tốc - thời gian: Đây là một đường thẳng có độ dốc tỉ lệ với gia tốc (\(\vec{a}\)). Đồ thị này giúp ta dễ dàng xác định gia tốc cũng như vận tốc tại mọi thời điểm.
- Đồ thị tọa độ - thời gian: Đây là một parabol, vì phương trình của tọa độ là một phương trình bậc hai theo thời gian.
Đồ thị vận tốc - thời gian và đồ thị tọa độ - thời gian đều cung cấp những thông tin quan trọng về quá trình chuyển động, giúp người học hiểu rõ hơn về bản chất của chuyển động thẳng biến đổi đều.
| Loại chuyển động | Quỹ đạo | Đặc điểm gia tốc |
|---|---|---|
| Chuyển động nhanh dần đều | Đường thẳng | Gia tốc cùng hướng với vận tốc |
| Chuyển động chậm dần đều | Đường thẳng | Gia tốc ngược hướng với vận tốc |
.png)
1. Tổng Quan Về Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều là một dạng chuyển động trong đó vật chuyển động theo đường thẳng với gia tốc không đổi. Gia tốc này có thể dương (vật tăng tốc) hoặc âm (vật giảm tốc), tùy thuộc vào hướng của lực tác dụng.
Chuyển động thẳng biến đổi đều có những đặc điểm chính như sau:
- Quỹ đạo: Vật di chuyển theo một đường thẳng.
- Vận tốc: Vận tốc của vật thay đổi đều đặn theo thời gian. Nếu gia tốc là dương, vận tốc tăng dần; nếu gia tốc là âm, vận tốc giảm dần.
- Gia tốc: Gia tốc \(a\) của vật là một hằng số và được xác định bằng công thức:
\[
a = \frac{\Delta v}{\Delta t}
\]
Trong đó:
- \(\Delta v\) là sự thay đổi vận tốc.
- \(\Delta t\) là khoảng thời gian thay đổi vận tốc.
Phương trình chuyển động của một vật trong chuyển động thẳng biến đổi đều được biểu diễn dưới dạng:
Trong đó:
- \(s\) là vị trí của vật tại thời điểm \(t\).
- \(s_0\) là vị trí ban đầu của vật.
- \(v_0\) là vận tốc ban đầu của vật.
- \(t\) là thời gian chuyển động.
- \(a\) là gia tốc của vật.
Đồ thị của chuyển động thẳng biến đổi đều có thể được biểu diễn dưới dạng đồ thị vận tốc-thời gian hoặc đồ thị vị trí-thời gian, giúp người học dễ dàng phân tích và hiểu rõ hơn về quá trình chuyển động của vật.
2. Phương Trình Chuyển Động Thẳng Biến Đổi Đều
Trong chuyển động thẳng biến đổi đều, phương trình chuyển động của một vật có thể được biểu diễn dưới dạng tổng quát, thể hiện mối quan hệ giữa vị trí, vận tốc, gia tốc và thời gian. Phương trình này giúp xác định vị trí của vật tại bất kỳ thời điểm nào trong quá trình chuyển động.
Phương trình chuyển động thẳng biến đổi đều được viết như sau:
Trong đó:
- \(s\) là vị trí của vật tại thời điểm \(t\).
- \(s_0\) là vị trí ban đầu của vật.
- \(v_0\) là vận tốc ban đầu của vật.
- \(t\) là thời gian chuyển động.
- \(a\) là gia tốc không đổi của vật.
Phương trình này cho phép ta tính toán vị trí của vật tại bất kỳ thời điểm nào, dựa trên các giá trị ban đầu \(s_0\), \(v_0\) và gia tốc \(a\). Nếu biết trước gia tốc và vận tốc ban đầu, ta có thể dự đoán chính xác sự thay đổi vị trí của vật theo thời gian.
Một dạng khác của phương trình chuyển động liên quan đến vận tốc của vật:
Trong đó:
- \(v\) là vận tốc của vật tại thời điểm \(t\).
- \(v_0\) là vận tốc ban đầu của vật.
- \(a\) là gia tốc không đổi.
Đây là phương trình cơ bản để xác định vận tốc của vật trong chuyển động thẳng biến đổi đều. Từ phương trình này, ta có thể suy ra vị trí của vật bằng cách tích hợp theo thời gian.

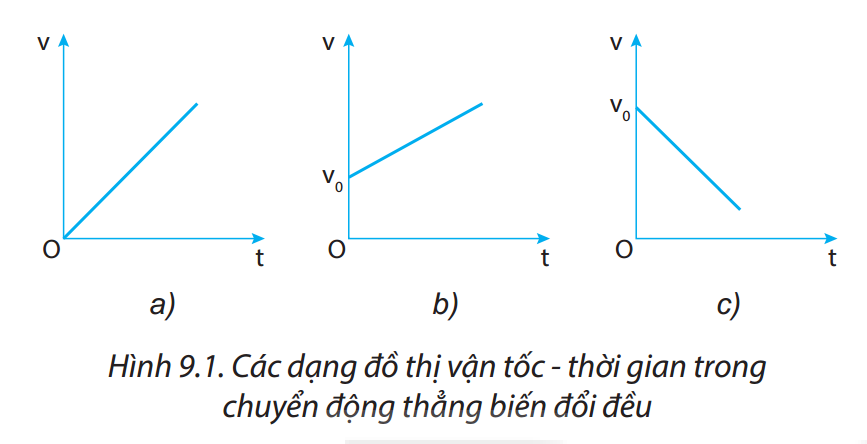
3. Đồ Thị Chuyển Động Thẳng Biến Đổi Đều
Đồ thị của chuyển động thẳng biến đổi đều là công cụ quan trọng để biểu diễn và phân tích sự thay đổi của các đại lượng vật lý theo thời gian. Đối với loại chuyển động này, có ba đồ thị chính cần xem xét: đồ thị vị trí - thời gian, đồ thị vận tốc - thời gian, và đồ thị gia tốc - thời gian.
3.1. Đồ Thị Vị Trí - Thời Gian
Đồ thị vị trí - thời gian mô tả sự thay đổi vị trí của vật theo thời gian. Đối với chuyển động thẳng biến đổi đều, đồ thị này là một parabol. Phương trình biểu diễn dưới dạng:
Đồ thị này có dạng một đường cong, cho thấy vị trí của vật tăng nhanh hoặc chậm tùy thuộc vào dấu của gia tốc.
3.2. Đồ Thị Vận Tốc - Thời Gian
Đồ thị vận tốc - thời gian là một đường thẳng, biểu diễn mối quan hệ tuyến tính giữa vận tốc và thời gian. Phương trình đồ thị:
Đường thẳng này có độ dốc bằng gia tốc \(a\), và nếu \(a > 0\), đường thẳng sẽ đi lên; nếu \(a < 0\), đường thẳng sẽ đi xuống. Đồ thị này giúp dễ dàng xác định vận tốc tại mọi thời điểm.
3.3. Đồ Thị Gia Tốc - Thời Gian
Đồ thị gia tốc - thời gian là một đường thẳng nằm ngang, thể hiện rằng gia tốc là không đổi theo thời gian:
Đồ thị này cho thấy gia tốc không thay đổi trong suốt quá trình chuyển động, với giá trị cố định và không bị ảnh hưởng bởi thời gian.
Nhìn chung, việc sử dụng đồ thị giúp ta hình dung rõ ràng hơn về chuyển động thẳng biến đổi đều, đồng thời tạo điều kiện thuận lợi cho việc phân tích và dự đoán hành vi của vật trong quá trình chuyển động.
4. Ứng Dụng Thực Tiễn Của Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống và công nghiệp. Dưới đây là một số ứng dụng cụ thể:
- Thiết kế hệ thống phanh xe: Trong các phương tiện giao thông, nguyên lý chuyển động thẳng biến đổi đều được áp dụng để thiết kế hệ thống phanh. Khi phanh gấp, xe giảm tốc độ một cách đều đặn, đảm bảo an toàn cho người lái và hành khách.
- Điều khiển động cơ: Trong công nghiệp, chuyển động thẳng biến đổi đều được sử dụng để điều khiển tốc độ động cơ trong các thiết bị máy móc, giúp duy trì hiệu suất làm việc ổn định và tiết kiệm năng lượng.
- Tính toán quãng đường di chuyển: Ứng dụng trong việc tính toán quãng đường mà một vật thể di chuyển với gia tốc không đổi. Phương trình chuyển động thẳng biến đổi đều giúp dự đoán chính xác vị trí và vận tốc của vật tại các thời điểm khác nhau.
- Kiểm soát giao thông: Trong giao thông, việc điều chỉnh tốc độ của các phương tiện để tránh tai nạn cũng dựa trên nguyên tắc của chuyển động thẳng biến đổi đều. Điều này giúp giảm thiểu nguy cơ va chạm và tăng cường an toàn trên đường.
- Thiết kế cầu đường: Khi thiết kế cầu hoặc đường cao tốc, các kỹ sư sử dụng nguyên lý chuyển động thẳng biến đổi đều để đảm bảo sự an toàn và thoải mái cho người tham gia giao thông, đặc biệt ở những đoạn có độ dốc hoặc đoạn đường cong.
Nhờ những ứng dụng này, chuyển động thẳng biến đổi đều trở thành một phần không thể thiếu trong việc phát triển các công nghệ hiện đại và cải thiện chất lượng cuộc sống.

5. Bài Tập Và Lời Giải Chuyển Động Thẳng Biến Đổi Đều
Dưới đây là một số bài tập về chuyển động thẳng biến đổi đều kèm theo lời giải chi tiết. Các bài tập này sẽ giúp bạn hiểu rõ hơn về lý thuyết và cách áp dụng vào thực tế.
- Bài tập 1: Một xe hơi bắt đầu chuyển động thẳng biến đổi đều từ trạng thái nghỉ với gia tốc \( a = 2 \, m/s^2 \). Tính quãng đường xe đi được sau \( t = 5 \, s \).
- Bài tập 2: Một vật chuyển động thẳng đều với vận tốc ban đầu \( v_0 = 10 \, m/s \) và gia tốc \( a = 3 \, m/s^2 \). Tính vận tốc của vật sau khi đã di chuyển được quãng đường \( S = 40 \, m \).
- Bài tập 3: Một người ném một quả bóng thẳng đứng lên cao với vận tốc ban đầu \( v_0 = 20 \, m/s \). Tính thời gian mà quả bóng đạt đến điểm cao nhất.
Lời giải: Sử dụng công thức tính quãng đường trong chuyển động thẳng biến đổi đều:
\[ S = \frac{1}{2} a t^2 \]Thay các giá trị đã cho vào:
\[ S = \frac{1}{2} \times 2 \, m/s^2 \times (5 \, s)^2 = 25 \, m \]Vậy quãng đường xe đi được là 25 mét.
Lời giải: Sử dụng công thức liên hệ giữa vận tốc, gia tốc và quãng đường:
\[ v^2 = v_0^2 + 2aS \]Thay các giá trị đã cho vào:
\[ v^2 = (10 \, m/s)^2 + 2 \times 3 \, m/s^2 \times 40 \, m = 100 + 240 = 340 \] \[ v = \sqrt{340} \approx 18.44 \, m/s \]Vậy vận tốc của vật sau khi di chuyển được 40 mét là khoảng 18,44 m/s.
Lời giải: Tại điểm cao nhất, vận tốc của quả bóng bằng 0. Sử dụng công thức:
\[ v = v_0 - g t \]Khi \( v = 0 \), ta có:
\[ 0 = 20 \, m/s - 9.8 \, m/s^2 \times t \] \[ t = \frac{20 \, m/s}{9.8 \, m/s^2} \approx 2.04 \, s \]Vậy thời gian để quả bóng đạt đến điểm cao nhất là khoảng 2,04 giây.
Thông qua việc giải các bài tập trên, bạn sẽ nắm vững hơn về cách áp dụng các công thức liên quan đến chuyển động thẳng biến đổi đều trong thực tế.