Các Công Thức Chuyển Động Thẳng Biến Đổi Đều: Tất Tần Tật Kiến Thức Bạn Cần Biết

Chuyển động thẳng biến đổi đều là chuyển động có gia tốc không đổi theo thời gian. Các công thức cơ bản của chuyển động thẳng biến đổi đều bao gồm:

1. Công Thức Tính Vận Tốc

Vận tốc tại một thời điểm bất kỳ được tính bằng công thức:

\[
v = v_0 + a \cdot t
\]

• \(v\): Vận tốc tại thời điểm \(t\) (m/s).
• \(v_0\): Vận tốc ban đầu (m/s).
• \(a\): Gia tốc (m/s²).
• \(t\): Thời gian (s).

2. Công Thức Tính Quãng Đường

Quãng đường đi được sau thời gian \(t\) được xác định bởi công thức:

\[
s = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2
\]

• \(s\): Quãng đường đi được (m).

3. Công Thức Liên Hệ Giữa Vận Tốc, Gia Tốc và Quãng Đường

Mối quan hệ giữa vận tốc, gia tốc và quãng đường được biểu diễn qua công thức:

\[
v^2 = v_0^2 + 2 \cdot a \cdot s
\]

4. Phương Trình Chuyển Động

Tọa độ của vật tại thời điểm \(t\) được tính theo phương trình:

\[
x = x_0 + v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2
\]

• \(x\): Tọa độ tại thời điểm \(t\) (m).
• \(x_0\): Tọa độ ban đầu (m).

5. Đặc Điểm Của Chuyển Động Thẳng Biến Đổi Đều

• Gia tốc không đổi trong suốt quá trình chuyển động.
• Đồ thị vận tốc - thời gian là một đường thẳng.
• Trong chuyển động nhanh dần đều, \(a\) và \(v_0\) cùng dấu; trong chuyển động chậm dần đều, \(a\) và \(v_0\) trái dấu.

Chuyển động thẳng biến đổi đều là dạng chuyển động trong đó vật di chuyển theo một đường thẳng với gia tốc không đổi. Điều này có nghĩa là vận tốc của vật thay đổi đều đặn theo thời gian, tức là mỗi giây trôi qua, vận tốc của vật tăng hoặc giảm một lượng bằng nhau.

Gia tốc trong chuyển động thẳng biến đổi đều có thể dương hoặc âm:

• Nếu gia tốc dương (\(a > 0\)), vận tốc của vật tăng dần theo thời gian. Đây được gọi là chuyển động thẳng nhanh dần đều.
• Nếu gia tốc âm (\(a < 0\)), vận tốc của vật giảm dần theo thời gian. Đây được gọi là chuyển động thẳng chậm dần đều.

Đặc điểm chính của chuyển động thẳng biến đổi đều bao gồm:

• Gia tốc \(a\) không thay đổi trong suốt quá trình chuyển động.
• Quỹ đạo của vật là một đường thẳng.
• Đồ thị vận tốc theo thời gian là một đường thẳng xiên (nếu gia tốc khác 0).

Các phương trình cơ bản mô tả chuyển động thẳng biến đổi đều bao gồm:

1. Phương trình vận tốc: \[ v = v_0 + a \cdot t \]
2. Phương trình quãng đường: \[ s = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 \]
3. Phương trình liên hệ giữa vận tốc, gia tốc và quãng đường: \[ v^2 = v_0^2 + 2 \cdot a \cdot s \]

Chuyển động thẳng biến đổi đều được mô tả bởi các công thức cơ bản liên quan đến vận tốc, quãng đường, và gia tốc. Dưới đây là các công thức quan trọng giúp bạn hiểu rõ hơn về loại chuyển động này.

1. Công Thức Tính Vận Tốc

Vận tốc của vật tại một thời điểm bất kỳ trong quá trình chuyển động được xác định bằng công thức:

\[
v = v_0 + a \cdot t
\]

• \(v\): Vận tốc tại thời điểm \(t\) (m/s).
• \(v_0\): Vận tốc ban đầu (m/s).
• \(a\): Gia tốc của vật (m/s²).
• \(t\): Thời gian chuyển động (s).

2. Công Thức Tính Quãng Đường

Quãng đường mà vật đi được sau thời gian \(t\) được tính theo công thức sau:

\[
s = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2
\]

• \(s\): Quãng đường đi được (m).
• \(v_0\): Vận tốc ban đầu (m/s).
• \(a\): Gia tốc của vật (m/s²).
• \(t\): Thời gian chuyển động (s).

3. Công Thức Liên Hệ Giữa Vận Tốc, Gia Tốc Và Quãng Đường

Mối quan hệ giữa vận tốc, gia tốc và quãng đường đi được được biểu diễn qua công thức:

\[
v^2 = v_0^2 + 2 \cdot a \cdot s
\]

• \(v\): Vận tốc tại thời điểm \(t\) (m/s).
• \(v_0\): Vận tốc ban đầu (m/s).
• \(a\): Gia tốc của vật (m/s²).
• \(s\): Quãng đường đi được (m).

4. Phương Trình Chuyển Động

Để xác định vị trí của vật tại một thời điểm bất kỳ, ta sử dụng phương trình chuyển động:

\[
x = x_0 + v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2
\]

• \(x\): Tọa độ của vật tại thời điểm \(t\) (m).
• \(x_0\): Tọa độ ban đầu của vật (m).
• \(v_0\): Vận tốc ban đầu (m/s).
• \(a\): Gia tốc của vật (m/s²).
• \(t\): Thời gian chuyển động (s).

Đồ thị là công cụ quan trọng để mô tả và phân tích chuyển động thẳng biến đổi đều. Dưới đây là các loại đồ thị phổ biến và cách đọc hiểu chúng.

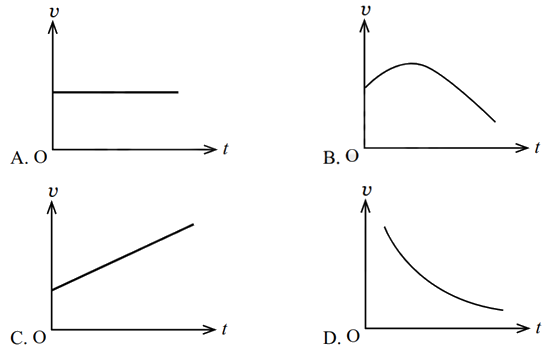
1. Đồ Thị Vận Tốc - Thời Gian (v - t)

Đồ thị vận tốc theo thời gian là một đường thẳng, đặc trưng cho gia tốc không đổi trong chuyển động thẳng biến đổi đều.

• Nếu đồ thị là một đường thẳng dốc lên, chuyển động là nhanh dần đều với gia tốc dương (\(a > 0\)).
• Nếu đồ thị là một đường thẳng dốc xuống, chuyển động là chậm dần đều với gia tốc âm (\(a < 0\)).
• Nếu đồ thị là một đường thẳng nằm ngang, vận tốc không thay đổi và gia tốc bằng không (\(a = 0\)).

Công thức liên hệ giữa vận tốc và thời gian trên đồ thị là:

\[
v = v_0 + a \cdot t
\]

2. Đồ Thị Gia Tốc - Thời Gian (a - t)

Đồ thị gia tốc theo thời gian trong chuyển động thẳng biến đổi đều là một đường thẳng nằm ngang, do gia tốc không đổi.

• Đồ thị nằm trên trục thời gian (trục \(t\)) khi gia tốc dương (\(a > 0\)), tức là vật đang tăng tốc.
• Đồ thị nằm dưới trục \(t\) khi gia tốc âm (\(a < 0\)), tức là vật đang giảm tốc.
• Đồ thị trùng với trục \(t\) khi gia tốc bằng 0 (\(a = 0\)), tức là vật chuyển động thẳng đều.

3. Đồ Thị Quãng Đường - Thời Gian (s - t)

Đồ thị quãng đường theo thời gian có dạng một parabol, do quãng đường đi được phụ thuộc vào bình phương thời gian khi có gia tốc không đổi.

• Đồ thị có dạng parabol hướng lên nếu chuyển động nhanh dần đều (\(a > 0\)).
• Đồ thị có dạng parabol hướng xuống nếu chuyển động chậm dần đều (\(a < 0\)).

Phương trình của đồ thị này là:

\[
s = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2
\]

Dưới đây là một số bài tập vận dụng về chuyển động thẳng biến đổi đều, giúp bạn củng cố kiến thức và áp dụng các công thức đã học vào thực tiễn. Hãy giải từng bài tập theo trình tự để hiểu rõ hơn về các khái niệm.

1. Bài Tập Tính Vận Tốc Và Quãng Đường

Bài tập 1: Một xe chuyển động thẳng nhanh dần đều từ trạng thái nghỉ với gia tốc \(a = 2 \, m/s^2\). Hãy tính vận tốc của xe sau 5 giây và quãng đường xe đi được trong thời gian đó.

Lời giải:

1. Tính vận tốc sau 5 giây: \[ v = v_0 + a \cdot t = 0 + 2 \cdot 5 = 10 \, m/s \]
2. Tính quãng đường đi được trong 5 giây: \[ s = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 = 0 + \frac{1}{2} \cdot 2 \cdot 5^2 = 25 \, m \]

2. Bài Tập Phương Trình Chuyển Động

Bài tập 2: Một vật chuyển động thẳng chậm dần đều với vận tốc ban đầu \(v_0 = 20 \, m/s\) và gia tốc \(a = -2 \, m/s^2\). Viết phương trình chuyển động của vật và xác định vị trí của vật sau 6 giây.

Lời giải:

1. Phương trình vận tốc: \[ v = v_0 + a \cdot t = 20 - 2 \cdot t \]
2. Phương trình chuyển động: \[ x = x_0 + v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 = x_0 + 20 \cdot t - \frac{1}{2} \cdot 2 \cdot t^2 \]
3. Xác định vị trí sau 6 giây: \[ x = x_0 + 20 \cdot 6 - \frac{1}{2} \cdot 2 \cdot 6^2 = x_0 + 120 - 36 = x_0 + 84 \, m \]

3. Bài Tập Tổng Hợp

Bài tập 3: Một vật bắt đầu chuyển động từ điểm \(A\) với vận tốc ban đầu \(v_0 = 5 \, m/s\) và gia tốc \(a = 3 \, m/s^2\). Tính quãng đường vật đi được và vận tốc của nó sau 4 giây. Sau đó, xác định thời gian vật đạt được vận tốc \(v = 17 \, m/s\).

Lời giải:

1. Quãng đường đi được sau 4 giây: \[ s = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 = 5 \cdot 4 + \frac{1}{2} \cdot 3 \cdot 4^2 = 20 + 24 = 44 \, m \]
2. Vận tốc sau 4 giây: \[ v = v_0 + a \cdot t = 5 + 3 \cdot 4 = 17 \, m/s \]
3. Thời gian để đạt được vận tốc \(17 \, m/s\): \[ t = \frac{v - v_0}{a} = \frac{17 - 5}{3} = 4 \, s \]

Chuyển động thẳng biến đổi đều là một trong những khái niệm cơ bản trong vật lý, nhưng nó có nhiều ứng dụng thiết thực trong đời sống và kỹ thuật. Dưới đây là một số ví dụ về cách áp dụng kiến thức này trong thực tiễn.

1. Thiết Kế Hệ Thống Phanh Trong Ô Tô

Hệ thống phanh trên ô tô sử dụng nguyên lý của chuyển động thẳng biến đổi đều để tính toán quãng đường và thời gian cần thiết để dừng xe an toàn khi có tác động của lực phanh. Điều này giúp cải thiện hiệu quả phanh và đảm bảo an toàn giao thông.

2. Tính Toán Quỹ Đạo Tên Lửa

Trong kỹ thuật hàng không và không gian, chuyển động thẳng biến đổi đều được áp dụng để tính toán quỹ đạo bay của tên lửa, giúp điều chỉnh gia tốc và vận tốc để đạt được độ cao và hướng bay mong muốn.

3. Điều Khiển Tốc Độ Của Thang Máy

Các hệ thống thang máy hiện đại thường sử dụng nguyên lý chuyển động thẳng biến đổi đều để điều chỉnh tốc độ, đảm bảo quá trình tăng tốc và giảm tốc diễn ra êm ái, mang lại trải nghiệm thoải mái và an toàn cho người dùng.

4. Ứng Dụng Trong Thiết Kế Đường Cao Tốc

Khi thiết kế đường cao tốc, kỹ sư sử dụng các công thức của chuyển động thẳng biến đổi đều để tính toán các đoạn tăng tốc, giảm tốc, giúp phương tiện di chuyển mượt mà, đồng thời đảm bảo an toàn cho các phương tiện khi nhập vào hoặc rời khỏi đường cao tốc.

5. Phân Tích Tai Nạn Giao Thông

Trong các vụ tai nạn giao thông, các chuyên gia thường sử dụng nguyên lý chuyển động thẳng biến đổi đều để phân tích hiện trường, tính toán vận tốc và quãng đường trước khi xảy ra va chạm, từ đó xác định nguyên nhân và trách nhiệm của các bên liên quan.