Chủ đề sơ đồ tư duy chuyển động tròn đều: Sơ đồ tư duy chuyển động tròn đều giúp bạn nắm vững các khái niệm vật lý một cách dễ dàng và trực quan. Hãy khám phá cách thức sử dụng sơ đồ tư duy để tối ưu hóa quá trình học tập của bạn, từ các định nghĩa cơ bản đến các công thức quan trọng.
Mục lục
Sơ Đồ Tư Duy Chuyển Động Tròn Đều
Chuyển động tròn đều là một dạng chuyển động trong đó một vật di chuyển theo quỹ đạo tròn với tốc độ góc không đổi. Để dễ dàng học tập và ghi nhớ, sử dụng sơ đồ tư duy là một phương pháp hiệu quả. Dưới đây là tóm tắt về sơ đồ tư duy liên quan đến chủ đề này.
1. Khái Niệm Chuyển Động Tròn Đều
- Chuyển động tròn đều là chuyển động theo quỹ đạo tròn với tốc độ không đổi.
- Tốc độ góc \(\omega\) được giữ nguyên trong suốt quá trình chuyển động.
- Quãng đường đi được trong một chu kỳ là chu vi của đường tròn: \[s = 2\pi r\]
2. Các Đại Lượng Đặc Trưng
- Tốc độ góc \(\omega = \frac{\Delta \theta}{\Delta t}\): Mô tả sự thay đổi góc quay theo thời gian.
- Gia tốc hướng tâm \[a_{ht} = \frac{v^2}{r} = \omega^2 r\]: Luôn hướng về tâm của quỹ đạo tròn.
- Lực hướng tâm \[F_{ht} = m \cdot a_{ht} = m \cdot \frac{v^2}{r}\]: Giữ cho vật di chuyển theo quỹ đạo tròn.
3. Ứng Dụng Thực Tiễn
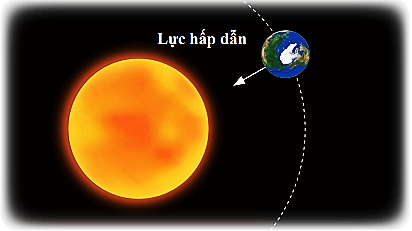
- Chuyển động của các hành tinh xung quanh mặt trời.
- Chuyển động của các electron trong nguyên tử theo quỹ đạo tròn.
- Chuyển động tròn của con lắc đồng hồ.
4. Sơ Đồ Tư Duy
| Khái niệm | Chuyển động tròn đều |
| Công thức liên quan | \(\omega = \frac{\Delta \theta}{\Delta t}\), \(a_{ht} = \frac{v^2}{r}\) |
| Ứng dụng | Quỹ đạo hành tinh, chuyển động electron, con lắc đồng hồ |
Việc sử dụng sơ đồ tư duy giúp học sinh dễ dàng hơn trong việc ghi nhớ và hiểu rõ các khái niệm, công thức của chuyển động tròn đều.

.png)
1. Khái Niệm Về Chuyển Động Tròn Đều
Chuyển động tròn đều là một dạng chuyển động trong đó một vật di chuyển theo quỹ đạo tròn với tốc độ không đổi. Điều này có nghĩa là vận tốc tuyến tính của vật trên quỹ đạo tròn là không đổi về độ lớn, mặc dù hướng của nó liên tục thay đổi theo thời gian.
Để hiểu rõ hơn, chúng ta cần phân tích các đại lượng đặc trưng của chuyển động tròn đều:
- Chu kỳ (\(T\)): Là thời gian mà vật đi hết một vòng trên quỹ đạo tròn. Chu kỳ được tính bằng công thức:
\[
T = \frac{2\pi r}{v}
\]
Trong đó:
- \(r\) là bán kính quỹ đạo tròn.
- \(v\) là vận tốc tuyến tính của vật.
- Tần số (\(f\)): Là số vòng mà vật đi được trong một đơn vị thời gian. Tần số được tính bằng công thức: \[ f = \frac{1}{T} \] Từ đó, ta có mối quan hệ giữa tần số và vận tốc góc: \[ \omega = 2\pi f \]
- Vận tốc góc (\(\omega\)): Là đại lượng mô tả tốc độ thay đổi của góc mà vật quét được trong một đơn vị thời gian, được tính bằng công thức: \[ \omega = \frac{\Delta \theta}{\Delta t} \]
Như vậy, chuyển động tròn đều có những đặc điểm sau:
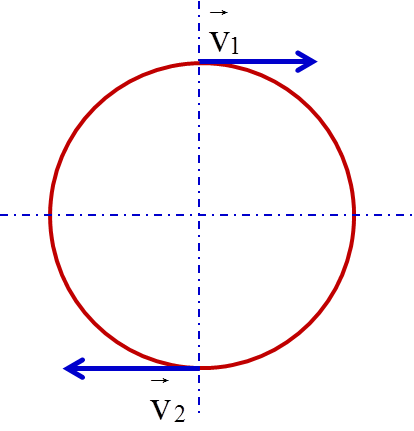
- Vận tốc tuyến tính \(v\) không đổi về độ lớn nhưng thay đổi về hướng.
- Vận tốc góc \(\omega\) là không đổi.
- Gia tốc hướng tâm \(a_{ht} = \frac{v^2}{r}\) luôn hướng về tâm của quỹ đạo tròn.
Chuyển động tròn đều có ứng dụng quan trọng trong nhiều lĩnh vực như cơ học, thiên văn học và cả trong cuộc sống hàng ngày, giúp chúng ta hiểu rõ hơn về các hiện tượng xoay quanh.
2. Các Công Thức Quan Trọng
Dưới đây là các công thức quan trọng trong chuyển động tròn đều mà bạn cần ghi nhớ:
- Chu kỳ (\(T\)): Thời gian để vật đi hết một vòng quỹ đạo tròn. Công thức tính chu kỳ:
\[
T = \frac{2\pi r}{v}
\]
Trong đó:
- \(r\) là bán kính quỹ đạo tròn.
- \(v\) là vận tốc tuyến tính của vật.
- Tần số (\(f\)): Số vòng quay được trong một đơn vị thời gian. Công thức tần số: \[ f = \frac{1}{T} \]
- Vận tốc tuyến tính (\(v\)): Độ lớn của vận tốc tại mỗi điểm trên quỹ đạo tròn, được tính bởi:
\[
v = \omega r
\]
Trong đó:
- \(\omega\) là vận tốc góc.
- \(r\) là bán kính quỹ đạo tròn.
- Vận tốc góc (\(\omega\)): Mức độ thay đổi của góc theo thời gian khi vật di chuyển trên quỹ đạo tròn: \[ \omega = \frac{\Delta \theta}{\Delta t} \]
- Gia tốc hướng tâm (\(a_{ht}\)): Gia tốc hướng về tâm của quỹ đạo, giữ cho vật di chuyển theo đường tròn: \[ a_{ht} = \frac{v^2}{r} = \omega^2 r \]
Các công thức này là cơ sở quan trọng để giải quyết các bài toán liên quan đến chuyển động tròn đều, từ việc tính toán quãng đường, vận tốc, đến các ứng dụng trong thực tế như động cơ quay, hành tinh quay quanh mặt trời.

3. Ứng Dụng Của Chuyển Động Tròn Đều
Chuyển động tròn đều có rất nhiều ứng dụng quan trọng trong đời sống hàng ngày và kỹ thuật. Dưới đây là một số ứng dụng chính:
- Trong cơ học: Chuyển động tròn đều được ứng dụng rộng rãi trong các thiết bị cơ khí như bánh xe, bánh răng, máy quay và các thiết bị quay khác. Tất cả đều dựa vào nguyên lý chuyển động tròn đều để duy trì hoạt động ổn định.
- Trong đồng hồ: Đồng hồ sử dụng chuyển động tròn đều của kim giây, kim phút và kim giờ để đo thời gian một cách chính xác.
- Trong công nghiệp: Các máy móc như máy tiện, máy phay và máy khoan đều sử dụng nguyên lý của chuyển động tròn đều để gia công vật liệu với độ chính xác cao.
- Trong thiên văn học: Quỹ đạo của các hành tinh xung quanh Mặt Trời, hay chuyển động của Mặt Trăng quanh Trái Đất, đều là những ví dụ của chuyển động tròn đều.
- Trong y học: Một số thiết bị chẩn đoán như máy MRI (Magnetic Resonance Imaging) cũng ứng dụng nguyên lý chuyển động tròn đều trong quá trình tạo hình ảnh.
Một ứng dụng khác là việc sử dụng chuyển động tròn đều để mô phỏng các hiện tượng tự nhiên, chẳng hạn như mô hình hóa quỹ đạo của vệ tinh hoặc chuyển động của chất lỏng trong các thiết bị ly tâm.

4. Lợi Ích Của Sử Dụng Sơ Đồ Tư Duy
Sử dụng sơ đồ tư duy mang lại nhiều lợi ích quan trọng trong quá trình học tập và làm việc, đặc biệt khi xử lý các khái niệm phức tạp như chuyển động tròn đều. Dưới đây là một số lợi ích chính:
- Cải thiện khả năng ghi nhớ: Sơ đồ tư duy giúp tổ chức thông tin một cách trực quan, làm tăng khả năng ghi nhớ thông tin qua việc liên kết các ý tưởng một cách logic và dễ hiểu.
- Phát triển tư duy sáng tạo: Sơ đồ tư duy khuyến khích tư duy mở rộng, giúp khám phá các mối quan hệ giữa các khái niệm, từ đó kích thích sự sáng tạo và khả năng giải quyết vấn đề.
- Dễ dàng tổng hợp và tóm tắt thông tin: Thay vì ghi chép dài dòng, sơ đồ tư duy cho phép tóm tắt các ý chính một cách ngắn gọn và dễ nhìn, giúp người học nắm bắt thông tin nhanh chóng và hiệu quả.
- Hỗ trợ việc trình bày và thuyết trình: Sơ đồ tư duy là công cụ hữu hiệu để trình bày các ý tưởng một cách rõ ràng và mạch lạc, giúp người nghe dễ dàng theo dõi và hiểu nội dung được trình bày.
- Tiết kiệm thời gian: Việc tạo ra sơ đồ tư duy nhanh chóng và hiệu quả hơn so với cách ghi chép truyền thống, giúp tiết kiệm thời gian trong quá trình học tập và làm việc.
Với những lợi ích trên, sơ đồ tư duy đã trở thành một công cụ quan trọng trong việc học tập và nghiên cứu, giúp người học nắm vững kiến thức và phát triển kỹ năng tư duy một cách toàn diện.

5. Cách Vẽ Sơ Đồ Tư Duy Chuyển Động Tròn Đều
Để vẽ sơ đồ tư duy cho chuyển động tròn đều, bạn có thể thực hiện theo các bước chi tiết sau đây:
-
Xác định chủ đề trung tâm:
Chủ đề trung tâm của sơ đồ tư duy này là "Chuyển Động Tròn Đều". Bạn có thể viết hoặc vẽ biểu tượng của chuyển động tròn đều ở giữa trang giấy.
-
Vẽ các nhánh chính:
Từ chủ đề trung tâm, vẽ các nhánh chính bao gồm các khía cạnh quan trọng của chuyển động tròn đều như:
- Định nghĩa và đặc điểm
- Công thức tính toán
- Các đại lượng liên quan
- Ứng dụng thực tế
-
Bổ sung các chi tiết vào từng nhánh:
Trong mỗi nhánh chính, bạn có thể vẽ thêm các nhánh nhỏ để liệt kê các công thức và định nghĩa liên quan:
- Định nghĩa và đặc điểm: Giải thích chi tiết về quỹ đạo đường tròn và tính chất đều của chuyển động.
- Công thức tính toán: Công thức liên quan đến tốc độ góc \(\omega\), chu kỳ \(T\), và tần số \(f\).
- Các đại lượng liên quan: Gia tốc hướng tâm \(\vec{a}_h\) và mối liên hệ giữa vận tốc và tốc độ góc.
- Ứng dụng thực tế: Các ví dụ như chuyển động của vệ tinh xung quanh Trái Đất.
-
Sử dụng màu sắc và hình ảnh:
Để sơ đồ thêm sinh động, bạn có thể sử dụng màu sắc khác nhau cho từng nhánh và thêm các biểu tượng hoặc hình ảnh minh họa.
-
Kiểm tra và hoàn thiện:
Cuối cùng, bạn cần kiểm tra lại toàn bộ sơ đồ tư duy để đảm bảo rằng tất cả các khía cạnh của chuyển động tròn đều đã được đề cập đầy đủ và chính xác.