Chuyển Động Tròn Nhanh Dần Đều: Khái Niệm, Công Thức và Ứng Dụng Thực Tiễn

Chuyển động tròn nhanh dần đều là một trong những loại chuyển động quan trọng trong vật lý, thường được nghiên cứu trong các bài học về động học và cơ học. Đây là một dạng chuyển động trong đó vật thể di chuyển trên một quỹ đạo tròn và tốc độ góc của nó tăng dần theo thời gian. Loại chuyển động này thường xuất hiện trong các hệ thống cơ học, máy móc, và cả trong các hiện tượng thiên văn.

1. Tốc Độ Góc Trong Chuyển Động Tròn Nhanh Dần Đều

Tốc độ góc (\(\omega\)) là đại lượng đo bằng góc mà bán kính quét được trong một đơn vị thời gian. Đối với chuyển động tròn nhanh dần đều, tốc độ góc sẽ tăng dần theo thời gian do sự tác động của một lực gây ra gia tốc góc.

Trong đó:

• \(\omega\): tốc độ góc tại thời điểm \(t\)
• \(\omega_0\): tốc độ góc ban đầu
• \(\alpha\): gia tốc góc
• \(t\): thời gian

2. Gia Tốc Góc và Gia Tốc Hướng Tâm

Gia tốc góc (\(\alpha\)) là đại lượng đặc trưng cho sự thay đổi tốc độ góc của vật thể theo thời gian. Trong chuyển động tròn nhanh dần đều, gia tốc góc là hằng số dương.

Gia tốc hướng tâm (\(a_{ht}\)) là gia tốc hướng về tâm quỹ đạo của vật thể, được tính theo công thức:

Trong đó:

• \(v\): tốc độ dài của vật thể
• \(r\): bán kính quỹ đạo

3. Các Công Thức Liên Quan

Chuyển động tròn nhanh dần đều có liên quan mật thiết đến nhiều công thức khác nhau trong vật lý. Dưới đây là một số công thức tiêu biểu:

• Chu kỳ (\(T\)): Thời gian để vật thể hoàn thành một vòng quỹ đạo. Công thức: \(T = \frac{2\pi}{\omega}\)
• Tần số (\(f\)): Số vòng quay mà vật thể thực hiện được trong một giây. Công thức: \(f = \frac{1}{T}\)
• Liên hệ giữa tốc độ dài và tốc độ góc: \(v = \omega \cdot r\)

4. Ứng Dụng Thực Tế

Chuyển động tròn nhanh dần đều xuất hiện trong nhiều lĩnh vực khác nhau, từ việc mô tả chuyển động của các hành tinh xung quanh mặt trời đến các ứng dụng trong kỹ thuật như động cơ quay, máy gia tốc, và thiết kế cơ khí. Hiểu rõ về loại chuyển động này giúp chúng ta tối ưu hóa các thiết kế và cải thiện hiệu suất của các thiết bị cơ học.

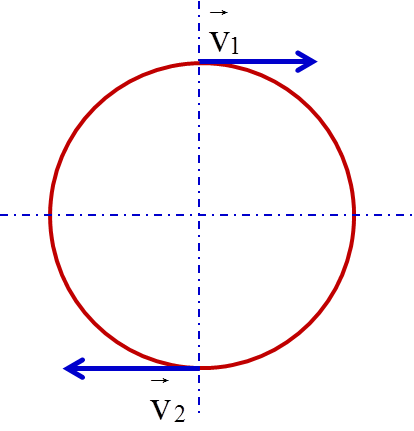
Chuyển động tròn nhanh dần đều là một dạng chuyển động trong đó một vật thể di chuyển trên quỹ đạo tròn với tốc độ góc tăng dần theo thời gian. Đặc điểm của chuyển động này là sự tăng lên của tốc độ góc \(\omega\) và gia tốc hướng tâm \({{a}_{ht}}\).

Trong chuyển động tròn nhanh dần đều, gia tốc góc \(\alpha\) là một hằng số dương, và vận tốc góc \(\omega\) tại một thời điểm bất kỳ được xác định bởi phương trình:

\[\omega = \omega_0 + \alpha \cdot t\]

Trong đó:

• \(\omega_0\): Vận tốc góc ban đầu
• \(\alpha\): Gia tốc góc, đơn vị rad/s²
• \(t\): Thời gian chuyển động

Quỹ đạo của vật trong chuyển động tròn nhanh dần đều là một đường tròn có bán kính không đổi, tuy nhiên, tốc độ góc và gia tốc hướng tâm sẽ thay đổi liên tục. Công thức tính gia tốc hướng tâm \({{a}_{ht}}\) là:

\[{a}_{ht} = \omega^2 \cdot r\]

Với:

• \(\omega\): Vận tốc góc tại thời điểm bất kỳ
• \(r\): Bán kính quỹ đạo

Như vậy, trong chuyển động tròn nhanh dần đều, vận tốc và gia tốc đều tăng lên, tạo nên một chuyển động ngày càng nhanh hơn dọc theo quỹ đạo tròn.

Trong chuyển động tròn nhanh dần đều, có một số công thức quan trọng mà bạn cần ghi nhớ để giải quyết các bài toán liên quan. Những công thức này bao gồm:

• 1. Công Thức Tính Vận Tốc Góc:

Vận tốc góc \(\omega\) tại thời điểm \(t\) được tính theo công thức:

\[\omega = \omega_0 + \alpha \cdot t\]

Trong đó:

• \(\omega_0\): Vận tốc góc ban đầu (rad/s)
• \(\alpha\): Gia tốc góc (rad/s²)
• \(t\): Thời gian (s)
• 2. Công Thức Tính Gia Tốc Hướng Tâm:

Gia tốc hướng tâm \({a}_{ht}\) tại thời điểm bất kỳ được tính bằng công thức:

\[{a}_{ht} = \omega^2 \cdot r\]

Với:

• \(\omega\): Vận tốc góc tại thời điểm \(t\)
• \(r\): Bán kính quỹ đạo (m)
• 3. Công Thức Tính Quãng Đường Cung Tròn:

Quãng đường cung tròn \(s\) mà vật di chuyển được trong thời gian \(t\) là:

\[s = \omega_0 \cdot t + \frac{1}{2} \alpha \cdot t^2\]

Trong đó:

• \(s\): Quãng đường cung tròn (m)
• \(\omega_0\): Vận tốc góc ban đầu (rad/s)
• \(\alpha\): Gia tốc góc (rad/s²)
• \(t\): Thời gian (s)
• 4. Công Thức Tính Gia Tốc Toàn Phần:

Gia tốc toàn phần \(\vec{a}\) trong chuyển động tròn nhanh dần đều được xác định bởi:

\[\vec{a} = \vec{a}_h + \vec{a}_t\]

Với:

• \(\vec{a}_h\): Gia tốc hướng tâm
• \(\vec{a}_t\): Gia tốc tiếp tuyến (phụ thuộc vào gia tốc góc \(\alpha\))

Những công thức này là cơ sở quan trọng để phân tích và giải quyết các bài toán liên quan đến chuyển động tròn nhanh dần đều, giúp bạn hiểu rõ hơn về các khía cạnh khác nhau của chuyển động này.

Trong chuyển động tròn nhanh dần đều, chu kỳ và tần số là hai đại lượng quan trọng để mô tả đặc tính của chuyển động.

• Chu Kỳ (T):

Chu kỳ \(T\) là khoảng thời gian để vật đi hết một vòng trong chuyển động tròn. Đơn vị của chu kỳ là giây (s).

Công thức tính chu kỳ:

\[ T = \frac{2\pi}{\omega} \]

Trong đó:

• \(\omega\): Vận tốc góc (rad/s) tại thời điểm cụ thể
• Tần Số (f):

Tần số \(f\) là số vòng mà vật thực hiện được trong một đơn vị thời gian. Đơn vị của tần số là Hertz (Hz).

Công thức tính tần số:

\[ f = \frac{1}{T} = \frac{\omega}{2\pi} \]

Trong đó:

• \(T\): Chu kỳ (s)
• \(\omega\): Vận tốc góc (rad/s)

Chu kỳ và tần số là hai đại lượng có quan hệ nghịch đảo với nhau. Khi vận tốc góc tăng, chu kỳ giảm, và tần số tăng lên, điều này biểu hiện rõ ràng trong chuyển động tròn nhanh dần đều. Sự thay đổi của hai đại lượng này giúp xác định tính chất của chuyển động và đưa ra các phân tích chính xác trong các bài toán vật lý liên quan.

Chuyển động tròn nhanh dần đều là một dạng chuyển động có quỹ đạo là đường tròn, trong đó vận tốc góc của vật tăng dần theo thời gian. Để mô tả chuyển động này, chúng ta sử dụng các phương trình liên quan đến tốc độ góc, tốc độ dài, và gia tốc hướng tâm.

4.1 Phương Trình Tốc Độ Góc \(\omega(t)\)

Tốc độ góc \(\omega(t)\) là đại lượng đo lường mức độ thay đổi góc quay của vật theo thời gian. Trong chuyển động tròn nhanh dần đều, tốc độ góc tăng tuyến tính với thời gian:

\[
\omega(t) = \omega_0 + \alpha t
\]

Trong đó:

• \(\omega_0\) là tốc độ góc ban đầu (rad/s)
• \(\alpha\) là gia tốc góc (rad/s²)
• \(t\) là thời gian (s)

4.2 Phương Trình Tốc Độ Dài \(v(t)\)

Tốc độ dài \(v(t)\) là tốc độ của một điểm trên đường tròn. Nó có mối quan hệ trực tiếp với tốc độ góc qua bán kính \(R\) của quỹ đạo:

\[
v(t) = R \cdot \omega(t) = R \cdot (\omega_0 + \alpha t)
\]

Trong đó:

• \(R\) là bán kính của quỹ đạo tròn (m)
• Các đại lượng khác như đã được định nghĩa ở trên

4.3 Phương Trình Gia Tốc \(a(t)\)

Gia tốc của vật trong chuyển động tròn nhanh dần đều gồm hai thành phần: gia tốc hướng tâm và gia tốc tiếp tuyến. Tuy nhiên, trong nhiều trường hợp, gia tốc tổng hợp \(a(t)\) thường được chú trọng:

\[
a(t) = \sqrt{(R \cdot \alpha)^2 + (\omega(t))^2}
\]

Gia tốc hướng tâm \(a_{ht}(t)\) có công thức tính như sau:

\[
a_{ht}(t) = \frac{v(t)^2}{R} = \frac{R \cdot (\omega_0 + \alpha t)^2}{R}
\]

Gia tốc tiếp tuyến \(a_{tt}(t)\) có công thức là:

\[
a_{tt}(t) = R \cdot \alpha
\]

Dưới đây là một số bài tập thực hành liên quan đến chuyển động tròn nhanh dần đều. Các bài tập này sẽ giúp bạn củng cố kiến thức lý thuyết và ứng dụng vào việc giải quyết các tình huống thực tế.

5.1 Bài Tập Tính Tốc Độ Góc

1. Bài toán: Một vật chuyển động tròn nhanh dần đều trên một quỹ đạo có bán kính \(r = 30 \, \text{cm}\). Ban đầu vật có tốc độ góc \(\omega_0 = 0\), sau 5 giây, tốc độ góc của nó đạt \(\omega = 10 \, \text{rad/s}\). Tính gia tốc góc \(\alpha\).

   Giải:

   • Gia tốc góc được tính bằng công thức: \[ \alpha = \frac{\omega - \omega_0}{t} = \frac{10 - 0}{5} = 2 \, \text{rad/s}^2 \]

5.2 Bài Tập Tính Gia Tốc Hướng Tâm

1. Bài toán: Một chiếc xe đạp đang chuyển động trên quỹ đạo tròn với vận tốc dài \(v = 36 \, \text{km/h}\), bán kính quỹ đạo là \(r = 0,5 \, \text{m}\). Tính gia tốc hướng tâm của chiếc xe.

   Giải:

   • Đổi \(v\) sang đơn vị \(\text{m/s}\): \[ v = 36 \, \text{km/h} = 10 \, \text{m/s} \]
   • Gia tốc hướng tâm được tính bằng công thức: \[ a_{ht} = \frac{v^2}{r} = \frac{10^2}{0,5} = 200 \, \text{m/s}^2 \]

5.3 Bài Tập Về Chu Kỳ và Tần Số

1. Bài toán: Một đĩa tròn có bán kính \(r = 20 \, \text{cm}\) quay đều và hoàn thành một vòng trong thời gian \(T = 0,4 \, \text{s}\). Tính tần số và tốc độ góc của đĩa.

   Giải:

   • Tần số \(f\) được tính bằng công thức: \[ f = \frac{1}{T} = \frac{1}{0,4} = 2,5 \, \text{Hz} \]
   • Tốc độ góc \(\omega\) được tính bằng công thức: \[ \omega = 2\pi f = 2\pi \times 2,5 = 15,7 \, \text{rad/s} \]

5.4 Bài Tập Tính Tốc Độ Dài và So Sánh

1. Bài toán: Một đĩa tròn quay đều với bán kính \(r = 40 \, \text{cm}\). Điểm A nằm trên vành ngoài và điểm B nằm trên trung điểm bán kính của đĩa. Tính tốc độ dài của hai điểm này và so sánh chúng.

   Giải:

   • Giả sử tốc độ góc của đĩa là \(\omega = 10 \, \text{rad/s}\).
   • Tốc độ dài của điểm A: \[ v_A = \omega r_A = 10 \times 0,4 = 4 \, \text{m/s} \]
   • Tốc độ dài của điểm B: \[ v_B = \omega r_B = 10 \times 0,2 = 2 \, \text{m/s} \]
   • So sánh: \[ \frac{v_A}{v_B} = \frac{4}{2} = 2 \]

5.5 Bài Tập Nâng Cao

1. Bài toán: Một hạt điện tử chuyển động tròn trong máy gia tốc có bán kính \(r = 1 \, \text{m}\). Thời gian để hạt hoàn thành 5 vòng quay là \(t = 5 \times 10^{-7} \, \text{s}\). Tính tốc độ góc, tốc độ dài và gia tốc hướng tâm của hạt.

   Giải:

   • Chu kỳ \(T\) cho một vòng quay: \[ T = \frac{t}{5} = \frac{5 \times 10^{-7}}{5} = 1 \times 10^{-7} \, \text{s} \]
   • Tốc độ góc: \[ \omega = \frac{2\pi}{T} = \frac{2\pi}{1 \times 10^{-7}} = 2 \times 10^7 \, \text{rad/s} \]
   • Tốc độ dài: \[ v = \omega r = 2 \times 10^7 \times 1 = 2 \times 10^7 \, \text{m/s} \]
   • Gia tốc hướng tâm: \[ a_{ht} = \omega^2 r = (2 \times 10^7)^2 \times 1 = 4 \times 10^{14} \, \text{m/s}^2 \]

Chuyển động tròn nhanh dần đều không chỉ là khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong cuộc sống và công nghệ. Dưới đây là một số ví dụ tiêu biểu:

6.1 Trong Công Nghệ

• Máy ly tâm: Các thiết bị ly tâm trong phòng thí nghiệm sử dụng chuyển động tròn nhanh dần đều để tách các chất khác nhau, như việc tách các thành phần trong mẫu máu hoặc làm giàu uranium cho năng lượng hạt nhân. Lực hướng tâm tạo ra giúp các phần tử có khối lượng riêng khác nhau di chuyển và phân tách theo các lớp khác nhau.
• Động cơ điện: Trong các loại động cơ điện, đặc biệt là động cơ cảm ứng và động cơ đồng bộ, nguyên lý chuyển động tròn nhanh dần đều được áp dụng để gia tăng tốc độ quay từ khi khởi động đến khi đạt tốc độ ổn định.

6.2 Trong Giao Thông

• Thiết kế đường cua: Chuyển động tròn nhanh dần đều được ứng dụng trong thiết kế đường ô tô, đường sắt ở các đoạn cua. Độ nghiêng của mặt đường được điều chỉnh để tạo ra lực hướng tâm, giúp phương tiện không bị trượt khỏi đường khi vào cua với tốc độ cao.
• Hệ thống truyền động của ô tô: Chuyển động quay của các bánh xe khi tăng tốc hoặc giảm tốc là ví dụ điển hình của chuyển động tròn nhanh dần đều. Khi tài xế tăng ga, tốc độ góc của bánh xe tăng dần, tạo nên gia tốc tròn đồng đều.

6.3 Trong Vật Lý Thiên Văn

• Quỹ đạo các hành tinh và vệ tinh: Chuyển động của các vệ tinh nhân tạo quanh Trái Đất, hay các hành tinh quay quanh Mặt Trời, đều là các ví dụ điển hình của chuyển động tròn. Khi một vệ tinh mới được phóng lên, tốc độ của nó tăng dần để đạt đủ tốc độ cần thiết duy trì quỹ đạo.
• Chuyển động của các ngôi sao trong thiên hà: Trong các thiên hà, các ngôi sao cũng có sự quay quanh trung tâm thiên hà với tốc độ thay đổi theo khoảng cách. Hiện tượng này liên quan đến lực hấp dẫn và chuyển động tròn nhanh dần đều, giúp giữ các ngôi sao không bị văng ra khỏi thiên hà.

6.4 Trong Các Thiết Bị Giải Trí

• Tàu lượn siêu tốc: Các thiết kế tàu lượn siêu tốc sử dụng nguyên lý của chuyển động tròn nhanh dần đều để tạo ra cảm giác mạnh cho người chơi, đồng thời đảm bảo an toàn khi vượt qua các đoạn cua gấp và xoắn ốc.

Các ứng dụng của chuyển động tròn nhanh dần đều xuất hiện rộng rãi trong đời sống và công nghệ hiện đại, từ những thiết bị nhỏ bé trong phòng thí nghiệm đến các hiện tượng thiên văn phức tạp.