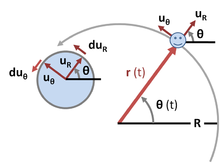
Chủ đề ví dụ về chuyển động tròn đều: Bài viết này cung cấp những ví dụ về chuyển động tròn đều, giúp bạn hiểu rõ khái niệm, công thức, và ứng dụng thực tế của chuyển động này. Với các minh họa và bài tập cụ thể, bạn sẽ nắm vững kiến thức về chuyển động tròn đều trong cuộc sống hàng ngày và trong khoa học kỹ thuật.
Mục lục
Ví Dụ Về Chuyển Động Tròn Đều
Chuyển động tròn đều là một dạng chuyển động trong đó một vật di chuyển theo một đường tròn với tốc độ không đổi. Dưới đây là một số ví dụ và thông tin chi tiết về chuyển động tròn đều:
1. Vận tốc Trong Chuyển Động Tròn Đều
Vận tốc của một vật trong chuyển động tròn đều có đặc điểm:
- Vận tốc có độ lớn không đổi nhưng luôn thay đổi về hướng.
- Phương của vận tốc luôn là tiếp tuyến với đường tròn tại mọi điểm.
Công thức tính vận tốc:
\(\vec{v} = \frac{\Delta \vec{s}}{\Delta t}\)
2. Tốc Độ Góc
Tốc độ góc là đại lượng đo bằng góc mà bán kính quét được trong một đơn vị thời gian.
Công thức tính tốc độ góc:
\(\omega = \frac{\Delta \alpha}{\Delta t}\)
3. Gia Tốc Hướng Tâm
Gia tốc hướng tâm là gia tốc luôn hướng vào tâm của quỹ đạo và được tính theo công thức:
\[a_{ht} = \frac{v^2}{r} = r\omega^2\]
4. Ví Dụ Thực Tế Về Chuyển Động Tròn Đều
- Chuyển động của Trái Đất quanh Mặt Trời: Đây là một ví dụ về chuyển động tròn đều với chu kỳ khoảng 365 ngày.
- Chuyển động của kim đồng hồ: Kim đồng hồ quay quanh trục với tốc độ góc không đổi.
- Chuyển động của bánh xe: Khi xe chạy với tốc độ ổn định, bánh xe thực hiện chuyển động tròn đều.
5. Ứng Dụng Của Chuyển Động Tròn Đều
Chuyển động tròn đều có nhiều ứng dụng trong đời sống và kỹ thuật, chẳng hạn như trong thiết kế các hệ thống truyền động, chế tạo máy móc, và cả trong các hiện tượng thiên văn học.

.png)
1. Khái Niệm Chuyển Động Tròn Đều
Chuyển động tròn đều là một dạng chuyển động mà trong đó một vật di chuyển theo quỹ đạo tròn với tốc độ không đổi. Đặc điểm chính của chuyển động này là tốc độ dài của vật không thay đổi, nhưng hướng của vận tốc lại thay đổi liên tục theo phương tiếp tuyến của quỹ đạo tròn.
Để hiểu rõ hơn, chúng ta có thể xem xét một số đặc điểm quan trọng của chuyển động tròn đều như sau:
- Quỹ đạo: Là một đường tròn có bán kính \(r\) không đổi.
- Tốc độ dài \(v\): Tốc độ dài của vật trong chuyển động tròn đều được xác định bằng công thức: \[ v = \frac{2\pi r}{T} \] trong đó \(T\) là chu kỳ quay, thời gian để vật di chuyển hết một vòng tròn.
- Tốc độ góc \(\omega\): Tốc độ góc là đại lượng đo bằng góc mà bán kính quét được trong một đơn vị thời gian và không đổi trong chuyển động tròn đều: \[ \omega = \frac{v}{r} = \frac{2\pi}{T} \]
- Gia tốc hướng tâm: Mặc dù tốc độ không đổi, nhưng do hướng vận tốc luôn thay đổi, vật chịu một gia tốc hướng tâm có độ lớn: \[ a_{ht} = \frac{v^2}{r} = r\omega^2 \] Gia tốc này luôn hướng về tâm của quỹ đạo tròn.
Như vậy, chuyển động tròn đều là một dạng chuyển động quan trọng trong cơ học, với nhiều ứng dụng thực tiễn như trong chuyển động của các hành tinh quanh Mặt Trời, cánh quạt máy bay, và các bộ phận quay trong máy móc.
2. Tốc Độ Góc và Gia Tốc Hướng Tâm
Trong chuyển động tròn đều, hai khái niệm quan trọng là tốc độ góc và gia tốc hướng tâm. Cả hai đều đóng vai trò then chốt trong việc mô tả chính xác chuyển động này.
Tốc Độ Góc (\(\omega\))
Tốc độ góc là đại lượng biểu thị góc mà bán kính quét được trong một đơn vị thời gian. Trong chuyển động tròn đều, tốc độ góc không thay đổi và được xác định bằng công thức:
\[
\omega = \frac{\Delta \theta}{\Delta t}
\]
trong đó \(\Delta \theta\) là góc quét được trong thời gian \(\Delta t\).
Mối quan hệ giữa tốc độ góc và tốc độ dài (\(v\)) được mô tả bởi công thức:
\[
\omega = \frac{v}{r}
\]
trong đó \(r\) là bán kính của quỹ đạo tròn.
Gia Tốc Hướng Tâm (\(a_{ht}\))
Gia tốc hướng tâm là gia tốc có phương luôn hướng vào tâm của quỹ đạo tròn, làm thay đổi hướng của vận tốc mà không thay đổi độ lớn của nó. Gia tốc hướng tâm được tính bằng công thức:
\[
a_{ht} = \frac{v^2}{r} = r\omega^2
\]
Gia tốc hướng tâm đóng vai trò quan trọng trong việc duy trì vật thể trên quỹ đạo tròn, ngăn không cho nó bay ra ngoài theo phương tiếp tuyến của quỹ đạo.
Như vậy, tốc độ góc và gia tốc hướng tâm là hai đại lượng quan trọng giúp phân tích và mô tả chuyển động tròn đều một cách chính xác và khoa học.

3. Ứng Dụng Của Chuyển Động Tròn Đều
Chuyển động tròn đều là hiện tượng phổ biến trong tự nhiên và đời sống, với nhiều ứng dụng quan trọng trong khoa học và công nghệ. Dưới đây là một số ví dụ tiêu biểu về ứng dụng của chuyển động tròn đều:
- Đồng hồ: Chuyển động của kim giây, kim phút và kim giờ trên đồng hồ là các ví dụ điển hình của chuyển động tròn đều. Kim giây, chẳng hạn, thực hiện một vòng quay mỗi 60 giây với tốc độ góc không đổi.
- Bánh xe: Chuyển động của bánh xe trên ô tô, xe đạp khi di chuyển với tốc độ ổn định cũng là một dạng chuyển động tròn đều. Các phương tiện này giữ tốc độ ổn định khi quay quanh trục, giúp xe di chuyển thẳng đều.
- Máy móc công nghiệp: Nhiều thiết bị trong công nghiệp, như cánh quạt, máy ly tâm, hay các động cơ quay, sử dụng chuyển động tròn đều để đảm bảo hoạt động liên tục và ổn định.
- Vũ trụ: Các vệ tinh nhân tạo di chuyển theo quỹ đạo tròn quanh Trái Đất, tạo ra các chuyển động tròn đều với tốc độ và khoảng cách nhất định, đảm bảo chúng luôn nằm trên quỹ đạo ổn định.
Những ứng dụng này không chỉ thể hiện tính chất của chuyển động tròn đều mà còn cho thấy tầm quan trọng của nó trong đời sống và công nghệ hiện đại.

XEM THÊM:
4. Các Bài Tập Minh Họa Về Chuyển Động Tròn Đều
Dưới đây là một số bài tập minh họa về chuyển động tròn đều, giúp bạn nắm vững kiến thức và áp dụng lý thuyết vào thực tiễn:
Bài Tập 1: Tính Tốc Độ Góc và Chu Kỳ Quay
Một chiếc quạt điện có cánh quạt dài 0,5m, quay đều với tốc độ 300 vòng/phút. Hãy tính:
- Tốc độ góc \(\omega\) của cánh quạt.
- Chu kỳ quay \(T\) của cánh quạt.
Giải:
- Đổi 300 vòng/phút sang vòng/giây: \[ f = \frac{300}{60} = 5 \text{ vòng/giây} \]
- Tính tốc độ góc: \[ \omega = 2\pi f = 2\pi \times 5 = 10\pi \, \text{rad/s} \]
- Chu kỳ quay: \[ T = \frac{1}{f} = \frac{1}{5} \, \text{giây} \]
Bài Tập 2: Gia Tốc Hướng Tâm
Một chiếc xe chuyển động tròn đều trên một đoạn đường cong bán kính 50m với tốc độ 20m/s. Hãy tính gia tốc hướng tâm của xe.
Giải:
- Tính gia tốc hướng tâm: \[ a_{ht} = \frac{v^2}{r} = \frac{20^2}{50} = 8 \, \text{m/s}^2 \]
Bài Tập 3: Tính Tốc Độ Dài
Một vệ tinh nhân tạo quay quanh Trái Đất trên quỹ đạo tròn với bán kính 7000km. Nếu chu kỳ quay của vệ tinh là 90 phút, hãy tính tốc độ dài của vệ tinh.
Giải:
- Đổi đơn vị chu kỳ quay: \[ T = 90 \times 60 = 5400 \, \text{giây} \]
- Tính tốc độ dài: \[ v = \frac{2\pi r}{T} = \frac{2\pi \times 7000 \times 10^3}{5400} \approx 814.44 \, \text{m/s} \]
Các bài tập trên không chỉ giúp củng cố kiến thức lý thuyết mà còn rèn luyện khả năng vận dụng vào các tình huống thực tiễn, từ đó nâng cao hiểu biết về chuyển động tròn đều.