Một vật nhỏ khối lượng 150g chuyển động tròn đều: Công thức và Ứng dụng thực tiễn

Trong bài toán vật lý, chúng ta thường gặp tình huống một vật nhỏ có khối lượng 150g chuyển động tròn đều. Dưới đây là những thông tin chi tiết liên quan đến chủ đề này.

Đặc điểm của chuyển động tròn đều

Chuyển động tròn đều là chuyển động của một vật trên một quỹ đạo tròn với tốc độ dài không đổi. Đặc điểm chính của chuyển động này là:

• Quỹ đạo: Là một đường tròn có bán kính xác định.
• Tốc độ dài: Không thay đổi trong quá trình chuyển động.
• Gia tốc hướng tâm: Luôn hướng về tâm của quỹ đạo tròn và có độ lớn được xác định bởi công thức \( a_{ht} = \frac{v^2}{r} \).

Công thức tính lực hướng tâm

Lực hướng tâm là lực tác dụng lên vật làm cho nó chuyển động tròn đều, luôn hướng về tâm của quỹ đạo tròn. Độ lớn của lực hướng tâm được tính bằng công thức:

\[
F_{ht} = m \cdot \frac{v^2}{r}
\]

Trong đó:

• \( F_{ht} \) là lực hướng tâm (N).
• \( m \) là khối lượng của vật (kg).
• \( v \) là tốc độ dài của vật (m/s).
• \( r \) là bán kính của quỹ đạo tròn (m).

Ví dụ minh họa

Giả sử một vật nhỏ có khối lượng \( 150g \) (\( m = 0.15 \, \text{kg} \)) chuyển động tròn đều với tốc độ dài \( v = 2 \, \text{m/s} \) trên quỹ đạo có bán kính \( r = 1.5 \, \text{m} \). Độ lớn của lực hướng tâm tác dụng lên vật được tính như sau:

\[
F_{ht} = 0.15 \cdot \frac{2^2}{1.5} = 0.4 \, \text{N}
\]

Ứng dụng của chuyển động tròn đều

Chuyển động tròn đều là nền tảng của nhiều ứng dụng trong thực tế, chẳng hạn như:

• Chuyển động của các hành tinh: Các hành tinh chuyển động tròn đều quanh Mặt Trời dưới tác dụng của lực hấp dẫn.
• Vòng quay trong các máy móc: Nhiều thiết bị cơ khí sử dụng chuyển động tròn đều để vận hành các bộ phận.

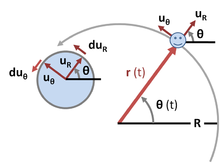
Chuyển động tròn đều là một dạng chuyển động mà một vật di chuyển trên một quỹ đạo tròn với tốc độ dài không đổi. Điều này có nghĩa là vật giữ nguyên tốc độ di chuyển dọc theo quỹ đạo, nhưng hướng của vận tốc thay đổi liên tục theo thời gian.

• Quỹ đạo: Quỹ đạo của chuyển động này là một đường tròn có bán kính cố định.
• Tốc độ dài: Tốc độ dài \(v\) của vật là không đổi và được tính bằng công thức: \[ v = \frac{s}{t} \] Trong đó, \(s\) là quãng đường vật đi được, và \(t\) là thời gian đi hết quãng đường đó.
• Gia tốc hướng tâm: Gia tốc này luôn hướng về tâm của quỹ đạo tròn và có độ lớn được xác định bởi công thức: \[ a_{ht} = \frac{v^2}{r} \] Trong đó, \(r\) là bán kính của quỹ đạo.
• Lực hướng tâm: Để duy trì chuyển động tròn đều, một lực hướng tâm \(F_{ht}\) phải tác động lên vật, lực này được tính bằng: \[ F_{ht} = m \cdot \frac{v^2}{r} \] Ở đây, \(m\) là khối lượng của vật.

Trong chuyển động tròn đều, mặc dù tốc độ dài của vật không thay đổi, nhưng vận tốc của vật lại thay đổi liên tục về hướng. Sự thay đổi liên tục này tạo ra một gia tốc hướng tâm, và để duy trì chuyển động này, lực hướng tâm phải luôn hiện diện.

Chuyển động tròn đều liên quan đến nhiều công thức tính toán quan trọng, giúp xác định các đại lượng vật lý như lực hướng tâm, tốc độ dài, tốc độ góc và gia tốc hướng tâm. Dưới đây là các công thức cơ bản và cách áp dụng chúng trong thực tế.

• Tốc độ dài \(v\): Tốc độ dài của vật trong chuyển động tròn đều được xác định bằng công thức: \[ v = \frac{s}{t} = r \cdot \omega \] Trong đó:
  • \(s\) là quãng đường vật đi được.
  • \(t\) là thời gian di chuyển.
  • \(r\) là bán kính của quỹ đạo tròn.
  • \(\omega\) là tốc độ góc của vật.
• Tốc độ góc \(\omega\): Tốc độ góc là đại lượng biểu thị tốc độ quay quanh tâm của vật và được tính bằng: \[ \omega = \frac{v}{r} \] hoặc \[ \omega = \frac{2\pi}{T} \] Trong đó:
  • \(T\) là chu kỳ quay, thời gian để vật thực hiện một vòng quay.
• Gia tốc hướng tâm \(a_{ht}\): Gia tốc này luôn hướng về tâm quỹ đạo và được tính bằng: \[ a_{ht} = \frac{v^2}{r} = \omega^2 \cdot r \]
• Lực hướng tâm \(F_{ht}\): Lực hướng tâm là lực giữ cho vật di chuyển trên quỹ đạo tròn đều, được xác định bởi: \[ F_{ht} = m \cdot a_{ht} = m \cdot \frac{v^2}{r} = m \cdot \omega^2 \cdot r \] Trong đó:
  • \(m\) là khối lượng của vật.

Những công thức trên không chỉ giúp tính toán các đại lượng vật lý cơ bản trong chuyển động tròn đều mà còn giúp phân tích sâu hơn về sự tương tác giữa các lực và chuyển động trong các hệ thống cơ học thực tế.

Dưới đây là một số bài toán ví dụ liên quan đến chuyển động tròn đều của một vật có khối lượng 150g. Các bài toán này giúp minh họa cách áp dụng các công thức đã học và cung cấp cái nhìn cụ thể hơn về hiện tượng vật lý này.

3.1. Bài toán 1: Tính lực hướng tâm

Đề bài: Một vật nhỏ có khối lượng \(150g\) chuyển động tròn đều với tốc độ dài \(v = 2 \, m/s\) trên quỹ đạo có bán kính \(r = 0.5 \, m\). Hãy tính lực hướng tâm tác dụng lên vật.

Giải:

• Khối lượng của vật: \(m = 0.15 \, kg\).
• Tốc độ dài: \(v = 2 \, m/s\).
• Bán kính quỹ đạo: \(r = 0.5 \, m\).

Áp dụng công thức tính lực hướng tâm:

Vậy, lực hướng tâm tác dụng lên vật là \(1.2 \, N\).

3.2. Bài toán 2: Tính tốc độ góc và gia tốc hướng tâm

Đề bài: Một vật có khối lượng \(150g\) chuyển động tròn đều trên một quỹ đạo với chu kỳ quay \(T = 4 \, s\) và bán kính quỹ đạo \(r = 1 \, m\). Tính tốc độ góc và gia tốc hướng tâm của vật.

Giải:

• Khối lượng của vật: \(m = 0.15 \, kg\).
• Chu kỳ quay: \(T = 4 \, s\).
• Bán kính quỹ đạo: \(r = 1 \, m\).

Áp dụng công thức tính tốc độ góc:

Áp dụng công thức tính gia tốc hướng tâm:

Vậy, tốc độ góc của vật là \(\frac{\pi}{2} \, rad/s\) và gia tốc hướng tâm là \(\frac{\pi^2}{4} \, m/s^2\).

3.3. Bài toán 3: Tính quãng đường đi được trong một khoảng thời gian

Đề bài: Một vật có khối lượng \(150g\) chuyển động tròn đều trên quỹ đạo bán kính \(r = 0.3 \, m\) với tốc độ góc \(\omega = 4 \, rad/s\). Hãy tính quãng đường vật đi được trong \(t = 5 \, s\).

Giải:

• Khối lượng của vật: \(m = 0.15 \, kg\).
• Bán kính quỹ đạo: \(r = 0.3 \, m\).
• Tốc độ góc: \(\omega = 4 \, rad/s\).
• Thời gian: \(t = 5 \, s\).

Áp dụng công thức tính tốc độ dài:

Quãng đường đi được sau \(t = 5 \, s\) là:

Vậy, quãng đường vật đi được trong \(5 \, s\) là \(6 \, m\).

Chuyển động tròn đều không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống và công nghệ. Dưới đây là một số ví dụ cụ thể về cách mà chuyển động tròn đều được ứng dụng trong thực tế.

• Máy quay ly tâm: Trong các phòng thí nghiệm và công nghiệp, máy quay ly tâm được sử dụng để tách các thành phần khác nhau trong một hỗn hợp bằng cách lợi dụng lực hướng tâm tạo ra từ chuyển động tròn đều. Các phần tử có khối lượng lớn hơn sẽ di chuyển ra ngoài xa hơn, trong khi các phần tử nhẹ hơn sẽ bị giữ lại ở gần tâm.
• Vệ tinh nhân tạo: Các vệ tinh quay quanh Trái Đất theo quỹ đạo tròn đều để duy trì vị trí ổn định. Chuyển động tròn đều giúp vệ tinh duy trì khoảng cách không đổi với Trái Đất, từ đó bảo đảm việc thu thập dữ liệu và truyền thông tin một cách liên tục.
• Hệ thống truyền động trong ô tô: Trong hệ thống truyền động của ô tô, chuyển động tròn đều được sử dụng để truyền lực từ động cơ đến các bánh xe. Các bánh răng quay tròn đều giúp xe di chuyển một cách ổn định và mượt mà.
• Các trò chơi trong công viên giải trí: Các trò chơi như đu quay, tàu lượn siêu tốc đều áp dụng nguyên lý của chuyển động tròn đều. Những trò chơi này tạo ra cảm giác mạnh mẽ và hấp dẫn nhờ lực hướng tâm và tốc độ góc lớn.
• Thiết bị gia dụng: Các thiết bị như máy giặt và máy sấy cũng hoạt động dựa trên nguyên lý chuyển động tròn đều. Lồng quay trong máy giặt giúp phân bổ nước và chất tẩy rửa đều quanh quần áo, đảm bảo hiệu quả làm sạch.

Nhờ những ứng dụng thực tiễn này, nguyên lý chuyển động tròn đều đã trở thành một phần không thể thiếu trong nhiều lĩnh vực, từ khoa học, công nghệ đến đời sống hàng ngày.

Chuyển động tròn đều của một vật nhỏ bị ảnh hưởng bởi nhiều yếu tố khác nhau. Việc hiểu rõ các yếu tố này giúp chúng ta có thể điều chỉnh và kiểm soát chuyển động trong các ứng dụng thực tế. Dưới đây là phân tích chi tiết về các yếu tố này.

• Bán kính quỹ đạo (\(r\)): Bán kính quỹ đạo ảnh hưởng trực tiếp đến tốc độ dài \(v\) và gia tốc hướng tâm \(a_{ht}\) của vật. Khi bán kính quỹ đạo tăng, tốc độ dài sẽ tăng nếu tốc độ góc không đổi. Công thức liên quan: \[ v = r \cdot \omega \] và \[ a_{ht} = \frac{v^2}{r} = \omega^2 \cdot r \]
• Tốc độ góc (\(\omega\)): Tốc độ góc là yếu tố quan trọng trong việc xác định tốc độ dài và gia tốc hướng tâm của vật. Khi tốc độ góc tăng, gia tốc hướng tâm cũng tăng. Công thức liên quan: \[ a_{ht} = \omega^2 \cdot r \]
• Khối lượng của vật (\(m\)): Khối lượng của vật ảnh hưởng đến lực hướng tâm \(F_{ht}\) cần thiết để duy trì chuyển động tròn đều. Lực hướng tâm tăng tuyến tính với khối lượng theo công thức: \[ F_{ht} = m \cdot a_{ht} = m \cdot \frac{v^2}{r} \]
• Lực ma sát: Lực ma sát giữa vật và bề mặt tác động có thể ảnh hưởng đến khả năng duy trì chuyển động tròn đều, đặc biệt là trong các hệ thống cơ học như bánh xe. Nếu lực ma sát quá lớn hoặc quá nhỏ, nó có thể làm mất cân bằng và dẫn đến việc vật trượt hoặc dừng lại.
• Lực tác dụng ngoài: Bất kỳ lực nào tác dụng ngoài (như gió, lực từ, hoặc lực đẩy) đều có thể gây ra biến đổi trong chuyển động tròn đều. Những lực này có thể làm thay đổi tốc độ góc, quỹ đạo hoặc thậm chí làm ngừng chuyển động của vật.

Những yếu tố này cần được xem xét kỹ lưỡng khi phân tích hoặc thiết kế các hệ thống cơ học và động lực học liên quan đến chuyển động tròn đều.

6.1. Bài tập trắc nghiệm

Dưới đây là một số câu hỏi trắc nghiệm về chuyển động tròn đều để bạn tự luyện tập:

1. Một vật nhỏ có khối lượng 150g chuyển động tròn đều với tốc độ góc \(\omega = 5 \, \text{rad/s}\) trên một quỹ đạo có bán kính \(r = 2 \, \text{m}\). Tính tốc độ dài của vật.
2. Một vật chuyển động tròn đều trên một quỹ đạo có bán kính \(r = 0.5 \, \text{m}\) với tốc độ dài \(v = 10 \, \text{m/s}\). Tính gia tốc hướng tâm của vật.
3. Một vật có khối lượng \(m = 0.2 \, \text{kg}\) chuyển động tròn đều với vận tốc dài \(v = 4 \, \text{m/s}\) trên quỹ đạo có bán kính \(r = 1 \, \text{m}\). Tính lực hướng tâm tác dụng lên vật.

6.2. Bài tập tự luận

Bài tập tự luận dưới đây giúp bạn hiểu sâu hơn về các khái niệm và công thức liên quan đến chuyển động tròn đều:

1. Một vật nhỏ có khối lượng 150g chuyển động tròn đều trên một quỹ đạo có bán kính \(r = 0.5 \, \text{m}\). Biết lực hướng tâm tác dụng lên vật là \(F_{ht} = 3 \, \text{N}\). Hãy tính tốc độ dài và tốc độ góc của vật.
   Giải:
   • Sử dụng công thức tính lực hướng tâm: \[ F_{ht} = m \cdot \frac{v^2}{r} \]
   • Thay các giá trị đã cho vào công thức và giải phương trình để tìm \(v\): \[ 3 = 0.15 \cdot \frac{v^2}{0.5} \implies v = \sqrt{\frac{3 \cdot 0.5}{0.15}} \approx 3.16 \, \text{m/s} \]
   • Tính tốc độ góc \( \omega \) bằng công thức: \[ \omega = \frac{v}{r} = \frac{3.16}{0.5} \approx 6.32 \, \text{rad/s} \]
2. Một vật chuyển động tròn đều trên quỹ đạo có bán kính \(r = 1 \, \text{m}\) với tốc độ góc \(\omega = 2 \, \text{rad/s}\). Tính lực hướng tâm tác dụng lên vật nếu khối lượng của vật là \(m = 200 \, \text{g}\).
   Giải:
   • Sử dụng công thức tính lực hướng tâm: \[ F_{ht} = m \cdot r \cdot \omega^2 \]
   • Thay các giá trị đã cho vào công thức: \[ F_{ht} = 0.2 \cdot 1 \cdot (2)^2 = 0.8 \, \text{N} \]
3. Một vật có khối lượng \(m = 300 \, \text{g}\) chuyển động tròn đều với gia tốc hướng tâm \(a_{ht} = 4 \, \text{m/s}^2\) trên quỹ đạo có bán kính \(r = 1.5 \, \text{m}\). Tính lực hướng tâm tác dụng lên vật và tốc độ dài của nó.
   Giải:
   • Tính lực hướng tâm: \[ F_{ht} = m \cdot a_{ht} = 0.3 \cdot 4 = 1.2 \, \text{N} \]
   • Tính tốc độ dài \(v\) từ gia tốc hướng tâm: \[ a_{ht} = \frac{v^2}{r} \implies v = \sqrt{a_{ht} \cdot r} = \sqrt{4 \cdot 1.5} \approx 2.45 \, \text{m/s} \]