Vecto gia tốc của vật chuyển động tròn đều: Khám phá chi tiết và ứng dụng thực tiễn

Vecto gia tốc trong chuyển động tròn đều là một khái niệm quan trọng trong vật lý. Khi một vật thể di chuyển theo quỹ đạo tròn với vận tốc không đổi, vecto gia tốc của nó có đặc điểm sau:

• Vecto gia tốc hướng tâm: Vecto gia tốc của vật luôn hướng vào tâm của quỹ đạo tròn. Đây là loại gia tốc chịu trách nhiệm giữ cho vật chuyển động theo đường tròn thay vì di chuyển theo một đường thẳng.
• Độ lớn của vecto gia tốc: Độ lớn của vecto gia tốc được tính theo công thức: \[ a = \frac{v^2}{r} \] trong đó:
  • a: Độ lớn của gia tốc hướng tâm (m/s²)
  • v: Vận tốc của vật trên quỹ đạo tròn (m/s)
  • r: Bán kính của quỹ đạo tròn (m)
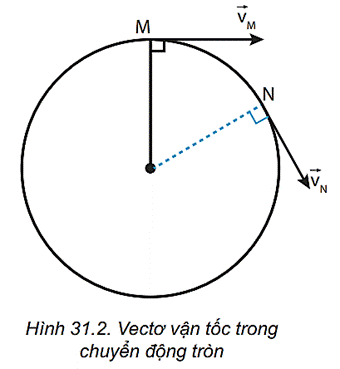
• Phương của vecto gia tốc: Phương của vecto gia tốc luôn vuông góc với vecto vận tốc của vật tại mọi điểm trên quỹ đạo. Điều này có nghĩa là vecto gia tốc không làm thay đổi độ lớn của vận tốc, mà chỉ thay đổi hướng của nó.

Trong chuyển động tròn đều, mặc dù tốc độ (độ lớn của vận tốc) không thay đổi, hướng của vận tốc luôn thay đổi, do đó vecto gia tốc không bằng không. Điều này cho thấy sự khác biệt giữa chuyển động thẳng đều và chuyển động tròn đều.

• Tính chất của vecto gia tốc: Vecto gia tốc có độ lớn không đổi và luôn hướng vào tâm của đường tròn. Công thức để tính vecto gia tốc trong chuyển động tròn đều cũng có thể được biểu diễn dưới dạng: \[ a = \omega^2 \times r \] trong đó:
  • \omega: Tốc độ góc của vật (rad/s)

Qua đó, ta thấy rằng vecto gia tốc là một thành phần quan trọng quyết định cách thức mà một vật di chuyển theo quỹ đạo tròn, duy trì chuyển động tròn đều của vật mà không bị lệch khỏi quỹ đạo.

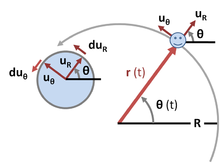
Trong chuyển động tròn đều, vecto gia tốc được hiểu là đại lượng biểu thị sự thay đổi của vecto vận tốc theo thời gian. Vecto này luôn có phương hướng về phía tâm của quỹ đạo tròn, và do đó được gọi là gia tốc hướng tâm. Công thức của vecto gia tốc trong chuyển động tròn đều được thể hiện như sau:

• Gia tốc hướng tâm: \[a_{ht} = \frac{v^2}{r} = r\omega^2\]

Trong đó:

• \(a_{ht}\) là gia tốc hướng tâm (m/s\(^2\))
• \(v\) là tốc độ dài của vật (m/s)
• \(\omega\) là tốc độ góc (rad/s)
• \(r\) là bán kính của quỹ đạo tròn (m)

Như vậy, gia tốc trong chuyển động tròn đều không làm thay đổi độ lớn của vận tốc mà chỉ thay đổi hướng của nó, luôn hướng vào tâm của quỹ đạo.

Trong chuyển động tròn đều, gia tốc của vật được gọi là gia tốc hướng tâm vì luôn hướng vào tâm của quỹ đạo tròn. Gia tốc này có thể được tính theo hai cách dựa trên các đại lượng khác nhau như vận tốc dài, tốc độ góc và bán kính quỹ đạo.

Công thức dựa trên vận tốc và bán kính

Gia tốc hướng tâm có thể được tính thông qua công thức sau:

\[ a_{ht} = \frac{v^2}{r} \]

• a_{ht}: Gia tốc hướng tâm (m/s²)
• v: Vận tốc dài của vật (m/s)
• r: Bán kính quỹ đạo tròn (m)

Công thức này cho thấy rằng gia tốc hướng tâm tỉ lệ thuận với bình phương của vận tốc và tỉ lệ nghịch với bán kính quỹ đạo.

Công thức dựa trên tốc độ góc và bán kính

Gia tốc hướng tâm cũng có thể được tính thông qua tốc độ góc \(\omega\) theo công thức:

\[ a_{ht} = \omega^2 \cdot r \]

• a_{ht}: Gia tốc hướng tâm (m/s²)
• \omega: Tốc độ góc (rad/s)
• r: Bán kính quỹ đạo tròn (m)

Trong công thức này, gia tốc hướng tâm tỉ lệ thuận với bình phương của tốc độ góc và với bán kính của quỹ đạo.

Kết luận

Cả hai công thức đều giúp chúng ta xác định gia tốc của vật chuyển động tròn đều, tùy thuộc vào thông tin có sẵn (vận tốc dài hoặc tốc độ góc). Gia tốc này luôn hướng vào tâm của quỹ đạo, đảm bảo vật chuyển động theo đường tròn mà không thoát ra ngoài quỹ đạo.

Chuyển động tròn đều là dạng chuyển động trong đó vật di chuyển trên một quỹ đạo tròn với tốc độ không đổi. Tuy nhiên, mặc dù tốc độ dài của vật là không đổi, nhưng do hướng của vận tốc liên tục thay đổi, nên chuyển động này sinh ra gia tốc. Dưới đây là những tính chất chính của chuyển động tròn đều:

• Quỹ đạo: Quỹ đạo của chuyển động tròn đều là một đường tròn, với bán kính \( r \) không đổi.
• Tốc độ dài: Tốc độ dài \( v \) của vật di chuyển trên quỹ đạo tròn được tính bằng công thức: \[ v = \frac{\Delta s}{\Delta t} \] trong đó \( \Delta s \) là cung tròn mà vật đi được trong khoảng thời gian \( \Delta t \). Tốc độ dài này không đổi trên mọi điểm của quỹ đạo.
• Tốc độ góc: Tốc độ góc \( \omega \) được định nghĩa là góc mà bán kính nối từ tâm đến vật quét được trong một đơn vị thời gian, và được tính bằng công thức: \[ \omega = \frac{\Delta \alpha}{\Delta t} \] trong đó \( \Delta \alpha \) là góc quét được trong thời gian \( \Delta t \). Tốc độ góc cũng là đại lượng không đổi trong chuyển động tròn đều.
• Chu kỳ và tần số:
  • Chu kỳ \( T \) là thời gian để vật đi được một vòng trên quỹ đạo tròn, được tính bằng công thức: \[ T = \frac{2\pi}{\omega} \]
  • Tần số \( f \) là số vòng mà vật đi được trong một giây, được tính bằng công thức: \[ f = \frac{1}{T} \]
• Gia tốc hướng tâm: Mặc dù tốc độ dài của vật là không đổi, nhưng hướng của vận tốc thay đổi liên tục, dẫn đến việc sinh ra một gia tốc có hướng vào tâm của quỹ đạo, gọi là gia tốc hướng tâm. Công thức tính gia tốc hướng tâm là: \[ a_{ht} = \frac{v^2}{r} = r\omega^2 \] trong đó \( v \) là tốc độ dài, \( r \) là bán kính quỹ đạo và \( \omega \) là tốc độ góc. Gia tốc hướng tâm luôn hướng vào tâm của quỹ đạo và có vai trò giữ cho vật tiếp tục di chuyển trên đường tròn.

Những tính chất trên không chỉ giúp ta hiểu rõ hơn về chuyển động tròn đều mà còn là nền tảng để giải quyết các bài toán liên quan đến chuyển động này trong thực tế.

Vecto gia tốc trong chuyển động tròn đều có nhiều ứng dụng trong đời sống và khoa học kỹ thuật. Dưới đây là một số ví dụ cụ thể và các bài tập giúp bạn hiểu rõ hơn về vai trò của vecto gia tốc trong các tình huống thực tế.

Ứng dụng thực tế của vecto gia tốc

• Ứng dụng trong thiết kế các thiết bị quay: Vecto gia tốc hướng tâm giúp các kỹ sư tính toán và thiết kế các bộ phận quay như bánh xe, tua bin, và các máy móc cần chuyển động tròn đều, đảm bảo chúng hoạt động ổn định mà không bị rung lắc hoặc hư hỏng do lực hướng tâm.
• Ứng dụng trong công nghệ vệ tinh: Vecto gia tốc hướng tâm giúp điều chỉnh quỹ đạo của vệ tinh nhân tạo xung quanh Trái Đất, giúp vệ tinh duy trì quỹ đạo ổn định và hoạt động chính xác theo yêu cầu.
• Ứng dụng trong thể thao: Trong các môn thể thao như đua xe, đua ngựa, và thậm chí trong các bài tập thể lực như xoay người, hiểu biết về vecto gia tốc giúp các vận động viên và huấn luyện viên cải thiện kỹ năng và hiệu suất thi đấu.

Bài tập tính vecto gia tốc trong các trường hợp cụ thể

1. Bài tập 1: Một vật di chuyển tròn đều với bán kính quỹ đạo \( r = 2 \, m \) và vận tốc dài \( v = 4 \, m/s \). Tính gia tốc hướng tâm của vật.

   Lời giải:

   Gia tốc hướng tâm được tính bằng công thức:

   \[ a_{ht} = \frac{v^2}{r} \]

   Thay các giá trị đã biết vào công thức:

   \[ a_{ht} = \frac{4^2}{2} = \frac{16}{2} = 8 \, m/s^2 \]
2. Bài tập 2: Một xe đua chuyển động trên đường đua hình tròn với bán kính \( r = 50 \, m \). Xe đua hoàn thành một vòng đua trong 20 giây. Hãy tính tốc độ góc và gia tốc hướng tâm của xe.

   Lời giải:

   Tốc độ góc được tính bằng công thức:

   \[ \omega = \frac{2\pi}{T} \]

   Thay \( T = 20 \, s \) vào công thức:

   \[ \omega = \frac{2\pi}{20} = \frac{\pi}{10} \, rad/s \]

   Gia tốc hướng tâm được tính bằng công thức:

   \[ a_{ht} = \omega^2 \times r = \left(\frac{\pi}{10}\right)^2 \times 50 = \frac{\pi^2 \times 50}{100} \approx 4.93 \, m/s^2 \]