Trong Một Chuyển Động Tròn Đều Vectơ Gia Tốc Là Gì? Hiểu Rõ Về Gia Tốc Hướng Tâm Và Ứng Dụng

Trong chuyển động tròn đều, một vật di chuyển trên quỹ đạo là một đường tròn với tốc độ không đổi. Vectơ gia tốc trong chuyển động này có đặc điểm rất đặc biệt và quan trọng. Dưới đây là các khái niệm cơ bản và công thức liên quan.

1. Tốc độ góc và tốc độ dài

• Tốc độ góc: Tốc độ góc \(\omega\) là đại lượng đo bằng góc mà bán kính quét được trong một đơn vị thời gian. Tốc độ góc của chuyển động tròn đều là không đổi. \[ \omega = \frac{\Delta \alpha}{\Delta t} \]
• Tốc độ dài: Tốc độ dài \(v\) là độ lớn của vận tốc tức thời của vật trên quỹ đạo tròn. Tốc độ dài cũng không đổi trong chuyển động tròn đều. \[ v = \frac{\Delta s}{\Delta t} \]

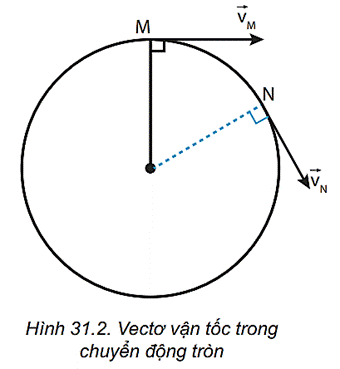
2. Vectơ vận tốc trong chuyển động tròn đều

Vectơ vận tốc của vật luôn có phương tiếp tuyến với quỹ đạo tròn tại mọi thời điểm. Do đó, khi vật di chuyển, hướng của vectơ vận tốc liên tục thay đổi nhưng độ lớn của nó thì không đổi.

3. Vectơ gia tốc hướng tâm

Trong chuyển động tròn đều, mặc dù tốc độ dài của vật không thay đổi, nhưng do hướng của vectơ vận tốc thay đổi liên tục, một gia tốc hướng tâm luôn tồn tại và hướng về tâm của quỹ đạo tròn. Gia tốc này có giá trị:
\[
a = \frac{v^2}{R} = \omega^2 R
\]
trong đó \(R\) là bán kính của quỹ đạo tròn.

4. Tổng quan về vectơ gia tốc

Vectơ gia tốc trong chuyển động tròn đều có đặc điểm là luôn hướng về tâm của quỹ đạo và có độ lớn không đổi. Điều này giải thích tại sao vật có thể duy trì chuyển động theo một quỹ đạo tròn mà không bị văng ra ngoài.

Chuyển động tròn đều là dạng chuyển động mà một vật di chuyển trên quỹ đạo hình tròn với tốc độ không đổi. Mặc dù tốc độ không thay đổi, nhưng hướng của vận tốc luôn thay đổi, dẫn đến sự tồn tại của một loại gia tốc đặc biệt gọi là gia tốc hướng tâm.

• Quỹ đạo: Quỹ đạo của chuyển động tròn đều là một đường tròn, có bán kính \( r \) không đổi.
• Vận tốc: Trong chuyển động tròn đều, vận tốc có độ lớn không đổi nhưng hướng của nó thay đổi liên tục. Vectơ vận tốc luôn tiếp tuyến với quỹ đạo tại mỗi điểm.
• Gia tốc: Gia tốc trong chuyển động tròn đều không gây ra sự thay đổi về độ lớn của vận tốc mà chỉ làm thay đổi hướng của nó. Vectơ gia tốc luôn hướng vào tâm của quỹ đạo tròn và được gọi là gia tốc hướng tâm.

Gia tốc hướng tâm \( a_{ht} \) được tính theo công thức:

Trong đó:

• \( v \) là tốc độ của vật
• \( r \) là bán kính quỹ đạo
• \( \omega \) là tốc độ góc của chuyển động

Như vậy, vectơ gia tốc hướng tâm luôn vuông góc với vectơ vận tốc và hướng vào tâm của quỹ đạo, đặc trưng cho sự thay đổi hướng của vận tốc trong chuyển động tròn đều.

Trong một chuyển động tròn đều, vật thể di chuyển trên một quỹ đạo hình tròn với tốc độ không đổi. Tuy nhiên, vì hướng của vận tốc liên tục thay đổi nên luôn tồn tại một gia tốc gọi là gia tốc hướng tâm.

Gia tốc này có một số đặc điểm như sau:

• Phương của vectơ gia tốc luôn hướng về tâm của quỹ đạo tròn.
• Độ lớn của vectơ gia tốc không thay đổi và được tính theo công thức: \[ a = \frac{v^2}{r} \] trong đó \(v\) là vận tốc của vật thể và \(r\) là bán kính của quỹ đạo tròn.
• Vectơ gia tốc có độ lớn tỉ lệ thuận với bình phương vận tốc và nghịch với bán kính quỹ đạo.
• Gia tốc hướng tâm không làm thay đổi độ lớn của vận tốc mà chỉ thay đổi hướng của vận tốc.

Chính sự tồn tại của gia tốc hướng tâm này khiến cho vật thể có thể duy trì được chuyển động tròn đều mà không bị văng ra ngoài.

Chuyển động tròn đều có rất nhiều ứng dụng trong thực tế, đặc biệt là trong các lĩnh vực kỹ thuật, công nghệ, và đời sống hàng ngày. Dưới đây là một số ứng dụng phổ biến của chuyển động tròn đều:

• Chuyển động của vệ tinh quanh Trái Đất: Các vệ tinh nhân tạo quay quanh Trái Đất theo quỹ đạo tròn đều với gia tốc hướng tâm giữ cho chúng ở đúng vị trí trong không gian. Điều này giúp duy trì hoạt động liên lạc, truyền hình và định vị toàn cầu.
• Chuyển động quay của động cơ: Trong các động cơ đốt trong, các piston thực hiện chuyển động tịnh tiến nhưng được chuyển đổi thành chuyển động quay đều của trục khuỷu, từ đó tạo ra lực quay cho các bánh xe của phương tiện.
• Quay đồng hồ cơ học: Trong đồng hồ cơ, chuyển động quay đều của các bánh răng giúp duy trì thời gian chính xác. Mỗi bánh răng chuyển động với tốc độ góc đều, đảm bảo kim đồng hồ chuyển động một cách đều đặn.
• Các trò chơi giải trí: Các vòng đu quay trong công viên giải trí hoạt động dựa trên nguyên tắc chuyển động tròn đều, mang lại trải nghiệm an toàn và thú vị cho người chơi.
• Máy ly tâm: Trong y học và công nghiệp, máy ly tâm sử dụng chuyển động tròn đều để tách các thành phần trong dung dịch theo tỷ lệ khối lượng, ứng dụng trong phân tích mẫu máu, tách dầu khỏi hỗn hợp và nhiều lĩnh vực khác.

Tất cả các ứng dụng này đều dựa trên nguyên lý chuyển động tròn đều với lực hướng tâm không đổi, giúp các vật thể duy trì quỹ đạo tròn quanh một trục cố định.

Dưới đây là một số bài tập thực hành và vận dụng để giúp bạn nắm vững hơn về chuyển động tròn đều và vectơ gia tốc trong các tình huống cụ thể:

• Bài tập 1: Một vật đang chuyển động tròn đều với bán kính quỹ đạo \(r = 2\)m và tốc độ góc \(\omega = 4\) rad/s. Hãy tính gia tốc hướng tâm của vật.

Giải: Sử dụng công thức gia tốc hướng tâm:

\[ a_{ht} = \omega^2 \cdot r = 4^2 \cdot 2 = 32 \, \text{m/s}^2 \]
• Bài tập 2: Xác định phương và chiều của vectơ gia tốc trong chuyển động tròn đều của một chiếc xe đang chạy trên đường tròn với tốc độ không đổi.

Giải: Vectơ gia tốc trong chuyển động tròn đều luôn hướng vào tâm của quỹ đạo và có phương vuông góc với vectơ vận tốc.

• Bài tập 3: Một hành khách trên vòng quay mặt trời có tốc độ tuyến tính là \(10\) m/s. Nếu bán kính của vòng quay là \(20\)m, hãy tính gia tốc hướng tâm của hành khách.

Giải: Sử dụng công thức gia tốc hướng tâm:

\[ a_{ht} = \frac{v^2}{r} = \frac{10^2}{20} = 5 \, \text{m/s}^2 \]
• Bài tập 4: Một quả bóng đang quay đều trên một sợi dây với tốc độ góc \(\omega = 3\) rad/s. Nếu dây có chiều dài \(l = 1\)m, hãy xác định gia tốc hướng tâm và mô tả chuyển động của quả bóng.

Giải: Gia tốc hướng tâm của quả bóng được tính như sau:

\[ a_{ht} = \omega^2 \cdot l = 3^2 \cdot 1 = 9 \, \text{m/s}^2

Việc luyện tập các bài tập này sẽ giúp bạn hiểu rõ hơn về chuyển động tròn đều và các khái niệm liên quan như vectơ gia tốc, vận tốc góc, và gia tốc hướng tâm.