Bài 31 Động Học Của Chuyển Động Tròn Đều: Kiến Thức Cơ Bản Và Ứng Dụng Thực Tế

Bài học này nằm trong chương trình Vật lý lớp 10 và thuộc chủ đề chuyển động tròn đều, một trong những chủ đề quan trọng giúp học sinh hiểu rõ về các khái niệm động học trong chuyển động tròn.

1. Khái niệm về chuyển động tròn đều

Chuyển động tròn đều là chuyển động của một vật trên một quỹ đạo hình tròn với tốc độ không đổi. Tốc độ góc, kí hiệu \(\omega\), là một đại lượng quan trọng mô tả chuyển động này. Công thức tính tốc độ góc là:

\[
\omega = \frac{\Delta \theta}{\Delta t}
\]
Trong đó:
\begin{align*}
\omega & : \text{Tốc độ góc (rad/s)} \\
\Delta \theta & : \text{Góc quay (rad)} \\
\Delta t & : \text{Thời gian quay (s)}
\end{align*}

2. Tính chất của chuyển động tròn đều

• Tốc độ dài \((v)\) của một điểm bất kỳ trên quỹ đạo tròn là không đổi và được tính bằng công thức: \[ v = \omega \cdot r \] trong đó \(r\) là bán kính quỹ đạo.
• Gia tốc hướng tâm \((a_t)\) luôn hướng về tâm của quỹ đạo tròn và có giá trị: \[ a_t = \frac{v^2}{r} = \omega^2 \cdot r \]
• Chu kỳ của chuyển động tròn đều, kí hiệu \(T\), là thời gian để vật thực hiện một vòng quay, được tính bằng công thức: \[ T = \frac{2\pi}{\omega} \]

3. Ứng dụng của chuyển động tròn đều

Chuyển động tròn đều có nhiều ứng dụng trong thực tế, như:

1. Chuyển động của các kim đồng hồ.
2. Chuyển động của các bánh xe trong máy móc và phương tiện giao thông.
3. Hoạt động của các thiết bị quay như quạt, máy giặt.

4. Bài tập liên quan

Để nắm vững lý thuyết, học sinh có thể thực hành các bài tập như tính toán tốc độ góc, gia tốc hướng tâm, hoặc phân tích chuyển động tròn đều của các vật trong đời sống thực tiễn.

5. Kết luận

Bài học về động học của chuyển động tròn đều không chỉ cung cấp kiến thức nền tảng quan trọng trong vật lý mà còn giúp học sinh hiểu rõ hơn về các hiện tượng xảy ra trong cuộc sống hàng ngày, từ đó áp dụng vào thực tế một cách hiệu quả.

Chuyển động tròn đều là chuyển động của một vật trên quỹ đạo hình tròn với tốc độ góc không đổi. Trong chuyển động tròn đều, tốc độ dài của vật không thay đổi, nhưng hướng của nó luôn thay đổi theo thời gian.

• Tốc độ góc \(\omega\) là đại lượng mô tả mức độ nhanh chậm của chuyển động quay, được định nghĩa bởi công thức: \[ \omega = \frac{\Delta \theta}{\Delta t} \] Trong đó:
  • \(\Delta \theta\) là góc quay trong khoảng thời gian \(\Delta t\).
  • \(\Delta t\) là thời gian cần thiết để quay một góc \(\Delta \theta\).
• Tốc độ dài \(v\) là vận tốc tuyến tính của vật tại một điểm trên quỹ đạo tròn, được tính bằng công thức: \[ v = \omega \cdot r \] Trong đó \(r\) là bán kính của quỹ đạo tròn.
• Chu kỳ \(T\) là thời gian để vật thực hiện một vòng quay, được xác định bởi: \[ T = \frac{2\pi}{\omega} \]
• Tần số \(f\) là số vòng quay trong một đơn vị thời gian, liên hệ với chu kỳ qua công thức: \[ f = \frac{1}{T} \]

Như vậy, chuyển động tròn đều là chuyển động mà trong đó vật chuyển động với tốc độ không đổi trên một quỹ đạo tròn, với các đại lượng chính là tốc độ góc, tốc độ dài, chu kỳ, và tần số.

Chuyển động tròn đều là chuyển động của một vật với tốc độ không đổi trên một đường tròn. Để mô tả chuyển động này, ta cần hiểu rõ các đại lượng cơ bản liên quan đến nó:

• Tần số (f): Đây là số vòng mà vật đi được trong một giây, đơn vị là hertz (Hz). Công thức: \(f = \frac{1}{T}\), trong đó \(T\) là chu kỳ.
• Chu kỳ (T): Thời gian để vật quay hết một vòng trên đường tròn, đơn vị là giây (s). Công thức: \(T = \frac{2\pi}{\omega}\).
• Tốc độ góc (ω): Đây là tốc độ quay của vật, đo bằng radian trên giây (rad/s). Công thức: \(\omega = \frac{\Delta \theta}{\Delta t}\), trong đó \(\Delta \theta\) là góc quét được trong thời gian \(\Delta t\).
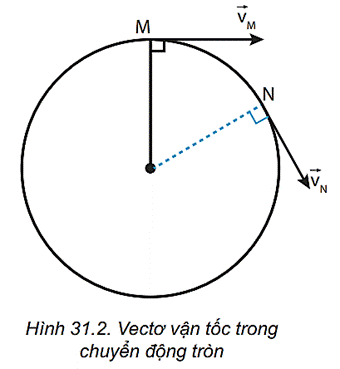
• Vận tốc dài (v): Đây là vận tốc của vật tại một điểm trên đường tròn, luôn tiếp tuyến với đường tròn. Công thức: \(v = \omega \cdot r\), trong đó \(r\) là bán kính của đường tròn.
• Gia tốc hướng tâm (a_ht): Đây là gia tốc khiến vật chuyển động theo hướng vào tâm của đường tròn. Công thức: \(a_ht = \frac{v^2}{r} = \omega^2 \cdot r\).

Các đại lượng này đều liên quan chặt chẽ với nhau, giúp ta hiểu rõ hơn về bản chất và đặc điểm của chuyển động tròn đều. Chúng đóng vai trò quan trọng trong việc tính toán và mô phỏng các hệ thống chuyển động trong thực tế.

Chuyển động tròn đều không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật. Dưới đây là một số ví dụ về các ứng dụng của chuyển động tròn đều:

• Máy móc quay: Các bộ phận như bánh xe, đĩa quay, và trục quay trong các loại máy móc công nghiệp đều hoạt động dựa trên nguyên lý chuyển động tròn đều. Việc duy trì tốc độ góc ổn định giúp các máy móc này hoạt động hiệu quả và bền bỉ.
• Chuyển động của hành tinh: Các hành tinh quay quanh mặt trời theo quỹ đạo gần tròn, với tốc độ góc gần như không đổi. Điều này là một ví dụ điển hình về chuyển động tròn đều trong vũ trụ.
• Máy quay ly tâm: Trong các phòng thí nghiệm, máy quay ly tâm được sử dụng để tách các chất có khối lượng khác nhau nhờ vào lực ly tâm sinh ra từ chuyển động tròn đều.
• Xe cộ di chuyển trên đường cong: Khi xe cộ di chuyển trên một đoạn đường cong (như đường cao tốc), chúng thực hiện chuyển động tròn đều. Vận tốc và gia tốc hướng tâm của xe cần được kiểm soát để tránh mất lái và đảm bảo an toàn.
• Vòng quay giải trí: Trong các công viên giải trí, vòng quay ngựa gỗ hoặc bánh xe Ferris là những ứng dụng tiêu biểu của chuyển động tròn đều, mang lại niềm vui và sự phấn khích cho người tham gia.

Những ứng dụng này cho thấy tầm quan trọng của việc hiểu biết về chuyển động tròn đều trong việc thiết kế, vận hành, và cải tiến các hệ thống cơ học và kỹ thuật trong cuộc sống hàng ngày.

Để giải các bài tập liên quan đến chuyển động tròn đều, bạn cần nắm vững các kiến thức cơ bản và áp dụng chúng một cách linh hoạt. Dưới đây là phương pháp giải bài tập bước từng bước:

1. Xác định đại lượng cần tính:
   • Đọc kỹ đề bài và xác định rõ yêu cầu, như cần tính tần số \(f\), chu kỳ \(T\), tốc độ góc \(\omega\), vận tốc dài \(v\), hoặc gia tốc hướng tâm \(a_{ht}\).
2. Viết các phương trình liên quan:
   • Liệt kê các phương trình cơ bản liên quan đến chuyển động tròn đều, ví dụ:
     • \(\omega = \frac{2\pi}{T}\)
     • \(v = \omega \cdot r\)
     • \(a_{ht} = \frac{v^2}{r} = \omega^2 \cdot r\)
3. Thay số và tính toán:
   • Thay giá trị cụ thể vào các phương trình và thực hiện tính toán từng bước. Đảm bảo các đơn vị của các đại lượng đồng nhất để tránh sai sót.
4. Kiểm tra kết quả:
   • Sau khi tính toán, kiểm tra lại các bước và kết quả xem có phù hợp với thực tế và yêu cầu của đề bài hay không.
   • Nếu cần, thực hiện lại các bước để đảm bảo tính chính xác.

Áp dụng phương pháp này sẽ giúp bạn tự tin hơn khi giải các bài tập liên quan đến chuyển động tròn đều, từ đó củng cố kiến thức và nâng cao kỹ năng giải bài tập vật lý.

5.1. Các câu hỏi trắc nghiệm về chuyển động tròn đều

Dưới đây là một số câu hỏi trắc nghiệm giúp củng cố kiến thức về chuyển động tròn đều:

1. Khi một vật chuyển động tròn đều, đại lượng nào sau đây là không đổi?
   • A. Gia tốc hướng tâm
   • B. Vận tốc dài
   • C. Tốc độ góc
   • D. Tất cả các đại lượng trên
2. Một vật chuyển động tròn đều có bán kính \(r = 0.5\) m và tốc độ góc \(\omega = 2\) rad/s. Tốc độ dài của vật là:
   • A. \(v = 1\) m/s
   • B. \(v = 2\) m/s
   • C. \(v = 1\pi\) m/s
   • D. \(v = 2\pi\) m/s
3. Gia tốc hướng tâm của một vật chuyển động tròn đều:
   • A. Luôn có phương tiếp tuyến với quỹ đạo
   • B. Luôn có phương vuông góc với bán kính quỹ đạo
   • C. Luôn có phương trùng với bán kính quỹ đạo
   • D. Luôn có phương vuông góc với vận tốc dài

5.2. Giải các bài tập tự luận cơ bản và nâng cao

Phần này cung cấp các bài tập tự luận, từ cơ bản đến nâng cao, giúp học sinh rèn luyện khả năng giải quyết vấn đề liên quan đến chuyển động tròn đều.

Bài tập 1: Tính tốc độ dài

Một vật chuyển động tròn đều trên quỹ đạo có bán kính \(r = 1\) m với tốc độ góc \(\omega = 5\) rad/s. Tính tốc độ dài của vật.

Giải:

Tốc độ dài \(v\) của vật được tính theo công thức:

Thay các giá trị vào công thức:

Vậy tốc độ dài của vật là \(5\) m/s.

Bài tập 2: Tính gia tốc hướng tâm

Một vật chuyển động tròn đều với tốc độ dài \(v = 3\) m/s trên quỹ đạo có bán kính \(r = 2\) m. Tính gia tốc hướng tâm của vật.

Giải:

Gia tốc hướng tâm \(a_{\text{ht}}\) được tính theo công thức:

Thay các giá trị vào công thức:

Vậy gia tốc hướng tâm của vật là \(4.5\) m/s².

Bài tập 3: Xác định lực hướng tâm

Một vật có khối lượng \(m = 0.5\) kg chuyển động tròn đều với tốc độ dài \(v = 4\) m/s trên quỹ đạo có bán kính \(r = 2\) m. Tính lực hướng tâm tác dụng lên vật.

Giải:

Lực hướng tâm \(F_{\text{ht}}\) được tính theo công thức:

Thay các giá trị vào công thức:

Vậy lực hướng tâm tác dụng lên vật là \(4\) N.