Chuyển động tròn đều là chuyển động: Hiểu rõ từ lý thuyết đến ứng dụng thực tiễn

Chuyển động tròn đều là một loại chuyển động cơ bản trong vật lý, thường được nghiên cứu trong chương trình học phổ thông. Đặc điểm của chuyển động tròn đều là vật thể chuyển động theo quỹ đạo tròn với tốc độ không đổi, tức là trong những khoảng thời gian bằng nhau, vật đi qua những cung tròn có độ dài bằng nhau.

Đặc điểm của chuyển động tròn đều

• Quỹ đạo: Quỹ đạo của chuyển động là một đường tròn.
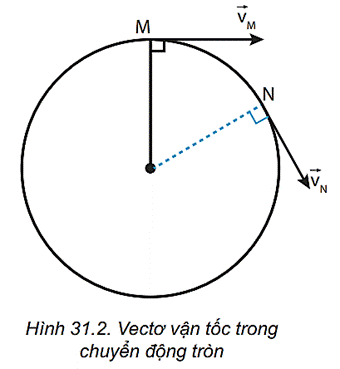
• Vận tốc: Vận tốc có độ lớn không đổi nhưng hướng của vận tốc luôn thay đổi theo tiếp tuyến của quỹ đạo tròn tại mỗi điểm.
• Gia tốc hướng tâm: Gia tốc này luôn hướng vào tâm của quỹ đạo và có giá trị được tính theo công thức: \[ a_{\text{ht}} = \frac{v^2}{r} = r\omega^2 \] trong đó:
  • \(v\) là tốc độ dài của vật (m/s)
  • \(\omega\) là tốc độ góc (rad/s)
  • \(r\) là bán kính quỹ đạo (m)

Công thức trong chuyển động tròn đều

• Tốc độ góc: Tốc độ góc là đại lượng đo bằng góc mà bán kính quỹ đạo quét được trong một đơn vị thời gian: \[ \omega = \frac{\Delta \alpha}{\Delta t} \]
• Chu kỳ: Chu kỳ \(T\) là thời gian để vật di chuyển hết một vòng quỹ đạo: \[ T = \frac{2\pi}{\omega} \]
• Tần số: Tần số \(f\) là số vòng mà vật đi được trong một giây: \[ f = \frac{1}{T} \]
• Công thức liên hệ giữa tốc độ dài và tốc độ góc: \[ v = \omega \times r \]

Bài tập minh họa

1.1. Định nghĩa chuyển động tròn đều

Chuyển động tròn đều là một loại chuyển động trong đó một vật di chuyển trên một quỹ đạo tròn với tốc độ góc không đổi. Tốc độ góc, ký hiệu là \(\omega\), là đại lượng đặc trưng cho sự thay đổi góc của bán kính quay theo thời gian. Trong chuyển động tròn đều, vận tốc của vật luôn có phương tiếp tuyến với quỹ đạo và có độ lớn không đổi.

1.2. Đặc điểm của chuyển động tròn đều

• Quỹ đạo: Chuyển động tròn đều xảy ra trên một quỹ đạo tròn.
• Tốc độ góc: Tốc độ góc \(\omega\) là hằng số và không thay đổi theo thời gian.
• Vận tốc: Vận tốc của vật có độ lớn không đổi nhưng luôn thay đổi hướng, phương tiếp tuyến với quỹ đạo.
• Gia tốc hướng tâm: Trong chuyển động tròn đều, vật luôn có một gia tốc hướng về tâm của quỹ đạo, gọi là gia tốc hướng tâm, được tính bằng công thức: \[ a = \frac{v^2}{r} = \omega^2 \cdot r \] trong đó \(v\) là vận tốc dài của vật, \(r\) là bán kính quỹ đạo.

1.3. Ví dụ minh họa về chuyển động tròn đều

Một ví dụ điển hình về chuyển động tròn đều là chuyển động của các hành tinh quanh Mặt Trời, chuyển động của các vệ tinh nhân tạo quanh Trái Đất, hay chuyển động của một điểm trên vành bánh xe khi xe chạy trên đường thẳng. Trong các trường hợp này, các vật đều di chuyển theo quỹ đạo tròn với tốc độ góc không đổi.

Chuyển động tròn đều là chuyển động trong đó vật di chuyển trên quỹ đạo tròn với tốc độ không đổi. Các đại lượng đặc trưng của chuyển động tròn đều bao gồm:

• Tốc độ góc (ω): Tốc độ góc là đại lượng cho biết góc mà bán kính quét được trong một đơn vị thời gian. Công thức tính tốc độ góc: \[ \omega = \frac{\Delta \theta}{\Delta t} \] trong đó \(\Delta \theta\) là góc quét trong khoảng thời gian \(\Delta t\). Đơn vị của tốc độ góc là radian/giây (rad/s).
• Tốc độ dài (v): Tốc độ dài là vận tốc của vật khi chuyển động trên quỹ đạo tròn. Nó được tính bằng công thức: \[ v = \omega \times R \] trong đó \(R\) là bán kính của quỹ đạo tròn. Đơn vị của tốc độ dài là mét/giây (m/s).
• Gia tốc hướng tâm (a_ht): Gia tốc hướng tâm là gia tốc mà vật phải chịu để duy trì chuyển động tròn đều. Gia tốc này luôn hướng về tâm của quỹ đạo tròn và được tính bằng công thức: \[ a_{ht} = \frac{v^2}{R} = \omega^2 \times R \] trong đó \(v\) là tốc độ dài và \(R\) là bán kính của quỹ đạo. Đơn vị của gia tốc hướng tâm là mét/giây^2 (m/s²).
• Chu kỳ (T): Chu kỳ là khoảng thời gian mà vật cần để hoàn thành một vòng trên quỹ đạo tròn. Chu kỳ được tính bằng công thức: \[ T = \frac{2\pi}{\omega} \] trong đó \(\omega\) là tốc độ góc. Đơn vị của chu kỳ là giây (s).
• Tần số (f): Tần số là số vòng mà vật hoàn thành được trong một đơn vị thời gian, ngược lại với chu kỳ và được tính bằng công thức: \[ f = \frac{1}{T} = \frac{\omega}{2\pi} \] Đơn vị của tần số là Hertz (Hz).

Các đại lượng trên không chỉ giúp mô tả chính xác chuyển động tròn đều mà còn là nền tảng để giải quyết các bài toán liên quan trong vật lý, từ đó giúp hiểu sâu hơn về các hiện tượng xảy ra trong tự nhiên.

Chuyển động tròn đều là một hiện tượng phổ biến trong tự nhiên và kỹ thuật, với nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau. Dưới đây là một số ví dụ minh họa về ứng dụng của chuyển động tròn đều trong thực tiễn:

3.1. Ứng dụng trong cơ học

Trong cơ học, chuyển động tròn đều là cơ sở để phân tích và thiết kế nhiều loại máy móc. Ví dụ, các bánh răng trong hộp số của ô tô hoạt động dựa trên nguyên lý của chuyển động tròn đều. Chúng giúp truyền động lực và thay đổi tốc độ của các bộ phận khác nhau trong hệ thống.

3.2. Ứng dụng trong thiên văn học

Chuyển động tròn đều cũng đóng vai trò quan trọng trong việc mô tả quỹ đạo của các hành tinh xung quanh mặt trời. Các hành tinh thực hiện chuyển động tròn đều với tốc độ góc không đổi trên quỹ đạo gần như tròn, giúp chúng ta tính toán và dự đoán vị trí của chúng trong vũ trụ.

3.3. Ứng dụng trong công nghệ

Trong lĩnh vực công nghệ, chuyển động tròn đều được áp dụng rộng rãi trong các thiết bị như quạt điện, bánh xe của rô bốt, và các thiết bị quay khác. Việc hiểu rõ nguyên lý của chuyển động tròn đều giúp tối ưu hóa hiệu suất và tuổi thọ của các thiết bị này.

Dưới đây là một số bài tập và câu hỏi thường gặp liên quan đến chuyển động tròn đều, giúp củng cố kiến thức và kỹ năng giải quyết các vấn đề trong chủ đề này:

4.1. Bài tập trắc nghiệm

• Câu 1: Phương và chiều của véc tơ vận tốc trong chuyển động tròn đều là gì?
  
  1. Phương tiếp tuyến với bán kính đường tròn quỹ đạo, chiều cùng chiều chuyển động.
  2. Phương vuông góc với bán kính đường tròn quỹ đạo, chiều cùng chiều chuyển động.
  3. Phương tiếp tuyến với bán kính đường tròn quỹ đạo, chiều ngược chiều chuyển động.
  4. Phương vuông góc với bán kính đường tròn quỹ đạo, chiều ngược chiều chuyển động.

  Đáp án: B

• Câu 2: Chuyển động nào có chu kỳ nhỏ hơn thì tốc độ góc sẽ như thế nào?
  
  1. Có tốc độ dài lớn hơn.
  2. Có tốc độ góc nhỏ hơn.
  3. Có tần số lớn hơn.
  4. Có bán kính nhỏ hơn.

  Đáp án: B

• Câu 3: Gia tốc hướng tâm của chất điểm chuyển động tròn đều sẽ thay đổi thế nào nếu vận tốc góc giảm còn một nửa nhưng bán kính quỹ đạo tăng gấp đôi?
  
  1. Không đổi.
  2. Tăng 4 lần.
  3. Tăng 2 lần.
  4. Giảm còn một nửa.

  Đáp án: A

4.2. Câu hỏi thường gặp

• Câu hỏi 1: Tại sao trong chuyển động tròn đều, tốc độ dài của vật không đổi nhưng gia tốc vẫn tồn tại?
  

  Giải thích: Trong chuyển động tròn đều, tốc độ dài của vật không đổi vì quỹ đạo là một đường tròn với bán kính không đổi. Tuy nhiên, gia tốc vẫn tồn tại vì phương của vận tốc luôn thay đổi, tạo ra một lực hướng tâm làm thay đổi hướng của vận tốc mà không thay đổi độ lớn của nó.

• Câu hỏi 2: Gia tốc hướng tâm trong chuyển động tròn đều được tính như thế nào?
  

  Giải thích: Gia tốc hướng tâm \( a_h \) trong chuyển động tròn đều được tính bằng công thức \( a_h = \frac{v^2}{R} = \omega^2 R \), trong đó \( v \) là tốc độ dài, \( R \) là bán kính của quỹ đạo, và \( \omega \) là tốc độ góc.

Chuyển động tròn đều là một hiện tượng vật lý cơ bản nhưng vô cùng quan trọng, xuất hiện nhiều trong thực tế và trong các ứng dụng kỹ thuật. Đây là loại chuyển động mà vật thể di chuyển trên một quỹ đạo tròn với tốc độ góc không đổi, dẫn đến việc vận tốc dài của vật cũng giữ nguyên nhưng luôn thay đổi về hướng.

Chuyển động tròn đều giúp chúng ta hiểu rõ hơn về các đặc điểm của các đại lượng như tốc độ dài, tốc độ góc, gia tốc hướng tâm và mối quan hệ giữa chúng. Đặc biệt, trong quá trình này:

• Vectơ vận tốc luôn tiếp tuyến với quỹ đạo tròn và có độ lớn không đổi.
• Tốc độ góc \(\omega\) là đại lượng không đổi và được liên kết chặt chẽ với tốc độ dài thông qua bán kính \(r\) của quỹ đạo: \(v = r \cdot \omega\).
• Gia tốc hướng tâm luôn hướng vào tâm của quỹ đạo, với công thức: \(a_{ht} = \frac{v^2}{r} = r \cdot \omega^2\).

Từ các công thức và khái niệm trên, có thể rút ra kết luận rằng chuyển động tròn đều là một mô hình đơn giản nhưng rất hữu ích trong việc phân tích các hệ thống cơ học. Nó cung cấp nền tảng vững chắc để nghiên cứu các chuyển động phức tạp hơn trong vật lý và kỹ thuật.