Vận tốc chuyển động tròn đều: Khám phá chi tiết và ứng dụng thực tế

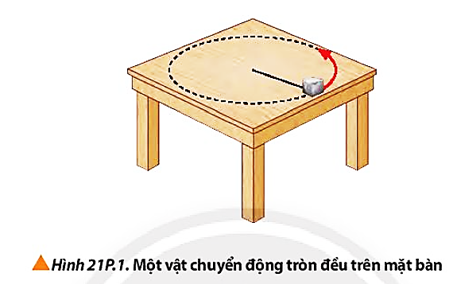
Chuyển động tròn đều là chuyển động của một vật trên quỹ đạo hình tròn với tốc độ dài không đổi. Trong chuyển động này, các đại lượng vận tốc dài, vận tốc góc, chu kỳ, tần số và gia tốc hướng tâm có mối liên hệ chặt chẽ với nhau thông qua các công thức toán học.

1. Vận tốc dài (\(v\))

Vận tốc dài là đại lượng đặc trưng cho tốc độ của một vật khi chuyển động dọc theo quỹ đạo tròn. Công thức tính vận tốc dài:

\[ v = \omega \times r \]

• \(v\): Vận tốc dài (m/s).
• \(\omega\): Vận tốc góc (rad/s).
• \(r\): Bán kính quỹ đạo (m).

2. Vận tốc góc (\(\omega\))

Vận tốc góc là đại lượng đo bằng góc mà bán kính quét được trong một đơn vị thời gian. Công thức tính vận tốc góc:

\[ \omega = \frac{\Delta \alpha}{\Delta t} \]

• \(\Delta \alpha\): Góc quay (rad).
• \(\Delta t\): Thời gian quay (s).

3. Chu kỳ (\(T\))

Chu kỳ là thời gian để vật đi được một vòng trên quỹ đạo tròn. Công thức tính chu kỳ:

\[ T = \frac{2\pi}{\omega} \]

• \(T\): Chu kỳ (s).

4. Tần số (\(f\))

Tần số là số vòng quay mà vật thực hiện được trong một giây. Công thức tính tần số:

\[ f = \frac{1}{T} \]

• \(f\): Tần số (Hz hoặc vòng/s).

5. Gia tốc hướng tâm (\(a_{ht}\))

Trong chuyển động tròn đều, gia tốc hướng tâm là đại lượng đặc trưng cho sự thay đổi hướng của vận tốc. Công thức tính gia tốc hướng tâm:

\[ a_{ht} = \frac{v^2}{r} = \omega^2 \times r \]

• \(a_{ht}\): Gia tốc hướng tâm (m/s²).

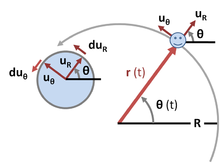
Chuyển động tròn đều là một loại chuyển động trong đó một vật di chuyển theo một quỹ đạo hình tròn với tốc độ dài không đổi. Đặc điểm nổi bật của chuyển động này là vận tốc của vật luôn có độ lớn không thay đổi nhưng hướng của nó thì liên tục thay đổi, tạo ra gia tốc hướng tâm.

Dưới đây là các đặc điểm chính của chuyển động tròn đều:

• Quỹ đạo: Quỹ đạo chuyển động là một đường tròn, bán kính \(r\) của quỹ đạo là không đổi.
• Vận tốc dài \(v\): Vận tốc dài của vật là tốc độ của vật dọc theo quỹ đạo tròn. Vận tốc này được tính bằng công thức: \[ v = \omega \times r \] trong đó \( \omega \) là vận tốc góc và \( r \) là bán kính quỹ đạo.
• Vận tốc góc \( \omega \): Vận tốc góc là tốc độ thay đổi góc của vật khi chuyển động quanh trục quay. Vận tốc góc được xác định bằng công thức: \[ \omega = \frac{\Delta \theta}{\Delta t} \] trong đó \( \Delta \theta \) là góc quét được và \( \Delta t \) là khoảng thời gian quét được góc đó.
• Chu kỳ \( T \): Chu kỳ là thời gian để vật đi hết một vòng quanh quỹ đạo tròn, được tính bằng công thức: \[ T = \frac{2\pi}{\omega} \]
• Tần số \( f \): Tần số là số vòng mà vật thực hiện trong một đơn vị thời gian, có mối liên hệ với chu kỳ qua công thức: \[ f = \frac{1}{T} \]
• Gia tốc hướng tâm \( a_{ht} \): Gia tốc hướng tâm là gia tốc luôn hướng về tâm của quỹ đạo tròn, có độ lớn được xác định bằng công thức: \[ a_{ht} = \frac{v^2}{r} = \omega^2 \times r \]

Nhờ các đặc điểm trên, chuyển động tròn đều là cơ sở để hiểu rõ hơn về các loại chuyển động phức tạp hơn, như chuyển động quay và chuyển động trong từ trường.

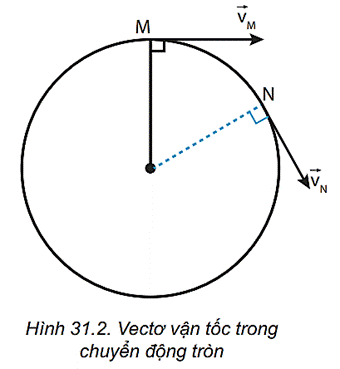
Trong chuyển động tròn đều, vận tốc của vật luôn là một đại lượng quan trọng và được chia thành hai loại: vận tốc dài và vận tốc góc. Chúng ta sẽ cùng tìm hiểu chi tiết từng loại vận tốc này và mối quan hệ giữa chúng.

2.1. Vận tốc dài (\(v\))

Vận tốc dài là tốc độ di chuyển của vật dọc theo quỹ đạo tròn và có độ lớn không đổi trong chuyển động tròn đều. Công thức tính vận tốc dài là:

\[ v = \frac{s}{t} \]

• \(v\) là vận tốc dài (m/s).
• \(s\) là quãng đường vật đi được trên quỹ đạo tròn (m).
• \(t\) là thời gian để đi hết quãng đường đó (s).

2.2. Vận tốc góc (\(\omega\))

Vận tốc góc là đại lượng đặc trưng cho tốc độ quay của vật quanh tâm quỹ đạo. Nó được tính bằng công thức:

\[ \omega = \frac{\Delta \theta}{\Delta t} \]

• \(\omega\) là vận tốc góc (rad/s).
• \(\Delta \theta\) là góc quay được trong khoảng thời gian \( \Delta t \) (rad).
• \(\Delta t\) là thời gian để quay được góc đó (s).

2.3. Mối quan hệ giữa vận tốc dài và vận tốc góc

Vận tốc dài và vận tốc góc có mối liên hệ chặt chẽ với nhau thông qua bán kính của quỹ đạo chuyển động. Công thức liên hệ giữa chúng là:

\[ v = \omega \times r \]

• \(v\) là vận tốc dài (m/s).
• \(\omega\) là vận tốc góc (rad/s).
• \(r\) là bán kính của quỹ đạo tròn (m).

2.4. Ví dụ minh họa

Giả sử một vật di chuyển tròn đều trên quỹ đạo có bán kính 2 m với vận tốc góc \( \omega = 5 \, \text{rad/s} \). Khi đó, vận tốc dài của vật được tính như sau:

\[ v = \omega \times r = 5 \times 2 = 10 \, \text{m/s} \]

Như vậy, vận tốc dài của vật là 10 m/s.

Trong chuyển động tròn đều, chu kỳ và tần số là hai đại lượng quan trọng đặc trưng cho sự lặp lại của chuyển động. Chúng có mối liên hệ mật thiết với nhau và đóng vai trò thiết yếu trong việc phân tích chuyển động này.

3.1. Chu kỳ (\(T\))

Chu kỳ là thời gian mà vật chuyển động để đi hết một vòng quanh quỹ đạo tròn. Chu kỳ của chuyển động tròn đều được tính theo công thức:

\[ T = \frac{2\pi}{\omega} \]

• \(T\) là chu kỳ (s).
• \(\omega\) là vận tốc góc (rad/s).

Chu kỳ cho biết thời gian cần thiết để vật hoàn thành một vòng quay đầy đủ, qua đó chúng ta có thể hiểu rõ hơn về tốc độ và nhịp độ của chuyển động tròn đều.

3.2. Tần số (\(f\))

Tần số là số vòng quay mà vật thực hiện được trong một đơn vị thời gian. Tần số có mối liên hệ nghịch đảo với chu kỳ và được tính bằng công thức:

\[ f = \frac{1}{T} = \frac{\omega}{2\pi} \]

• \(f\) là tần số (Hz hoặc vòng/s).
• \(T\) là chu kỳ (s).

Tần số cho biết mức độ thường xuyên của chuyển động lặp lại, từ đó giúp chúng ta xác định được tốc độ quay của vật trong chuyển động tròn đều.

3.3. Ví dụ minh họa

Giả sử một vật chuyển động tròn đều với vận tốc góc \( \omega = 4 \, \text{rad/s} \). Khi đó, chu kỳ và tần số của chuyển động này được tính như sau:

• Chu kỳ: \[ T = \frac{2\pi}{\omega} = \frac{2\pi}{4} = \frac{\pi}{2} \, \text{s} \]
• Tần số: \[ f = \frac{1}{T} = \frac{4}{2\pi} \, \text{Hz} \]

Như vậy, chu kỳ của chuyển động là \( \frac{\pi}{2} \) giây và tần số là \( \frac{2}{\pi} \) Hz.

Gia tốc hướng tâm là một yếu tố quan trọng trong chuyển động tròn đều, giúp giữ cho vật di chuyển theo quỹ đạo tròn mà không bị văng ra ngoài. Gia tốc này luôn hướng về tâm của quỹ đạo, tạo ra lực cần thiết để duy trì chuyển động tròn đều.

4.1. Khái niệm gia tốc hướng tâm

Gia tốc hướng tâm là gia tốc mà vector của nó luôn hướng vào tâm của quỹ đạo tròn. Đặc điểm của gia tốc này là chỉ làm thay đổi hướng của vận tốc, không làm thay đổi độ lớn của vận tốc, do đó vật vẫn di chuyển đều với một tốc độ không đổi.

4.2. Công thức tính gia tốc hướng tâm

Gia tốc hướng tâm có thể được tính bằng nhiều công thức khác nhau, phụ thuộc vào các đại lượng liên quan:

• Nếu biết vận tốc dài \(v\) và bán kính quỹ đạo \(r\), ta có công thức: \[ a_{ht} = \frac{v^2}{r} \]
• Nếu biết vận tốc góc \(\omega\) và bán kính quỹ đạo \(r\), ta có công thức: \[ a_{ht} = \omega^2 \times r \]

4.3. Vai trò của gia tốc hướng tâm trong chuyển động tròn đều

Gia tốc hướng tâm đóng vai trò quan trọng trong việc duy trì chuyển động tròn đều. Nó là nguyên nhân của lực hướng tâm, lực này giữ cho vật không bị bay ra khỏi quỹ đạo tròn. Trong các ứng dụng thực tế như trong chuyển động của các hành tinh, chuyển động của xe trên đường cong hay trong các trò chơi cảm giác mạnh, gia tốc hướng tâm là yếu tố quyết định để đảm bảo an toàn và ổn định cho chuyển động.

4.4. Ví dụ minh họa

Giả sử một chiếc xe đang di chuyển trên một khúc cua với bán kính 50 m và vận tốc 20 m/s. Gia tốc hướng tâm mà chiếc xe phải chịu sẽ được tính như sau:

\[ a_{ht} = \frac{v^2}{r} = \frac{20^2}{50} = 8 \, \text{m/s}^2 \]

Như vậy, gia tốc hướng tâm là 8 m/s², hướng về phía tâm của khúc cua.

Chuyển động tròn đều không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tế trong đời sống và kỹ thuật. Để hiểu rõ hơn về chuyển động này, chúng ta sẽ cùng tìm hiểu thông qua các bài tập và ví dụ minh họa thực tế.

5.1. Bài tập về chuyển động tròn đều

1. Bài tập 1: Một chiếc xe chuyển động tròn đều trên đường tròn có bán kính 100 m với vận tốc dài là 20 m/s. Hãy tính gia tốc hướng tâm của chiếc xe.

   Lời giải:

   Gia tốc hướng tâm được tính theo công thức:
   \[
   a_{ht} = \frac{v^2}{r}
   \]
   Trong đó \(v = 20 \, \text{m/s}\) và \(r = 100 \, \text{m}\). Do đó:
   \[
   a_{ht} = \frac{20^2}{100} = 4 \, \text{m/s}^2
   \]

2. Bài tập 2: Một vệ tinh nhân tạo quay quanh Trái Đất ở độ cao không đổi với chu kỳ 90 phút. Tính tần số quay của vệ tinh.

   Lời giải:

   Tần số quay được tính bằng công thức:
   \[
   f = \frac{1}{T}
   \]
   Trong đó \(T = 90 \, \text{phút} = 5400 \, \text{giây}\). Do đó:
   \[
   f = \frac{1}{5400} \approx 1.85 \times 10^{-4} \, \text{Hz}
   \]

5.2. Ứng dụng thực tế của chuyển động tròn đều

• Hệ thống truyền động bánh răng: Trong các máy móc cơ khí, các bánh răng quay tròn đều để truyền lực và chuyển động giữa các bộ phận, đảm bảo máy móc hoạt động hiệu quả và ổn định.

• Chuyển động của hành tinh: Các hành tinh trong hệ Mặt Trời di chuyển theo quỹ đạo tròn đều hoặc gần tròn, và chuyển động này tuân theo các định luật của cơ học cổ điển, đặc biệt là định luật vạn vật hấp dẫn.

• Các trò chơi cảm giác mạnh: Trong các trò chơi như đu quay, tàu lượn siêu tốc, chuyển động tròn đều tạo ra lực hướng tâm lớn, mang lại cảm giác mạnh mẽ và thú vị cho người chơi.

Qua các bài tập và ví dụ thực tế trên, chúng ta có thể thấy rằng chuyển động tròn đều không chỉ là một khái niệm cơ bản trong vật lý mà còn có rất nhiều ứng dụng trong đời sống và công nghệ.