Chuyển động nào sau đây là chuyển động tròn đều? Tìm hiểu chi tiết và các ví dụ minh họa

Khi tìm kiếm từ khóa "chuyển động nào sau đây là chuyển động tròn đều" trên Bing tại Việt Nam, bạn sẽ nhận được rất nhiều thông tin liên quan đến chủ đề này. Các trang web thường cung cấp kiến thức về chuyển động tròn đều, đặc điểm của chuyển động này, và các bài tập vật lý liên quan. Dưới đây là tổng hợp chi tiết:

1. Định nghĩa và đặc điểm của chuyển động tròn đều

Chuyển động tròn đều là loại chuyển động trong đó một vật di chuyển trên quỹ đạo hình tròn với tốc độ góc không đổi. Các đại lượng liên quan như chu kỳ \((T)\), tần số \((f)\), tốc độ góc \((\omega)\), và gia tốc hướng tâm \((a_{ht})\) được xác định bởi các công thức toán học cụ thể.

2. Công thức quan trọng

• Công thức chu kỳ: \( T = \frac{2\pi}{\omega} \)
• Công thức tần số: \( f = \frac{1}{T} \)
• Công thức liên hệ giữa tốc độ dài và tốc độ góc: \( v = r \cdot \omega \)
• Gia tốc hướng tâm: \( a_{ht} = \frac{v^2}{r} = r \cdot \omega^2 \)

3. Bài tập vận dụng

Các bài tập thường yêu cầu học sinh xác định các đại lượng như tốc độ dài, tốc độ góc, chu kỳ, tần số của một vật đang thực hiện chuyển động tròn đều. Ví dụ:

• Tính chu kỳ quay của một vệ tinh quanh Trái Đất.
• Xác định tốc độ dài của một điểm trên vành ngoài của bánh xe đạp khi xe chuyển động thẳng đều.

4. Các câu hỏi trắc nghiệm phổ biến

Các câu hỏi trắc nghiệm liên quan đến chuyển động tròn đều thường yêu cầu học sinh nhận diện các đặc điểm của chuyển động này hoặc áp dụng các công thức để tính toán các đại lượng liên quan. Ví dụ:

1. Quỹ đạo của chuyển động tròn đều có hình dạng như thế nào?
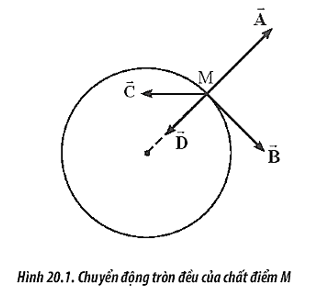
2. Vecto gia tốc của chuyển động tròn đều luôn hướng về đâu?
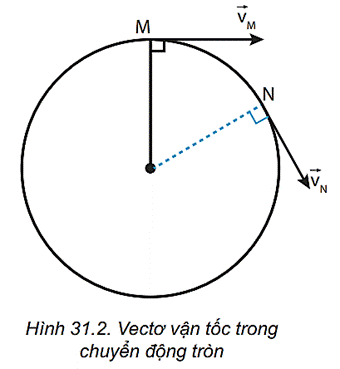
3. Vecto vận tốc của chuyển động tròn đều có đặc điểm gì?

5. Tài liệu và hướng dẫn học tập

Các trang web như VietJack, Học Thật Giỏi, Con Kẹc cung cấp rất nhiều tài liệu và hướng dẫn giải bài tập liên quan đến chuyển động tròn đều. Học sinh có thể tìm thấy lời giải chi tiết, công thức liên quan và các ví dụ minh họa để hiểu rõ hơn về chủ đề này.

6. Tính ứng dụng trong đời sống

Chuyển động tròn đều không chỉ là lý thuyết mà còn có nhiều ứng dụng thực tế như trong chuyển động của các hành tinh, vệ tinh nhân tạo, các bộ phận quay của máy móc như cánh quạt, bánh xe.

Tóm lại, từ khóa "chuyển động nào sau đây là chuyển động tròn đều" sẽ giúp bạn tìm kiếm được những thông tin cần thiết về khái niệm, công thức, và các bài tập liên quan đến chuyển động tròn đều, giúp bạn học tập và áp dụng tốt hơn trong thực tiễn.

Trong chuyển động tròn đều, có một số công thức quan trọng giúp xác định các đại lượng liên quan như chu kỳ, tần số, tốc độ dài, tốc độ góc, và gia tốc hướng tâm. Dưới đây là các công thức cơ bản và cách tính toán chúng.

• Chu kỳ \( T \): Chu kỳ là thời gian để vật di chuyển hết một vòng trên quỹ đạo tròn. Chu kỳ được tính bằng công thức: \[ T = \frac{2\pi}{\omega} \] trong đó, \(\omega\) là tốc độ góc.
• Tần số \( f \): Tần số là số vòng quay mà vật thực hiện trong một đơn vị thời gian. Tần số liên hệ với chu kỳ qua công thức: \[ f = \frac{1}{T} = \frac{\omega}{2\pi} \] Tần số được đo bằng Hertz (Hz), đại diện cho số vòng quay mỗi giây.
• Tốc độ góc \( \omega \): Tốc độ góc là đại lượng đo lường góc quay được trong một đơn vị thời gian. Công thức tính tốc độ góc là: \[ \omega = \frac{\Delta \theta}{\Delta t} \] với \(\Delta \theta\) là góc quay được trong khoảng thời gian \(\Delta t\).
• Tốc độ dài \( v \): Tốc độ dài của vật trong chuyển động tròn đều là tốc độ mà vật di chuyển dọc theo quỹ đạo tròn. Công thức tính tốc độ dài là: \[ v = r\omega \] trong đó, \(r\) là bán kính của quỹ đạo.
• Gia tốc hướng tâm \( a_{ht} \): Trong chuyển động tròn đều, dù tốc độ dài không đổi nhưng vật vẫn có gia tốc hướng tâm do sự thay đổi hướng của vecto vận tốc. Gia tốc hướng tâm được tính bằng: \[ a_{ht} = \frac{v^2}{r} = r\omega^2 \] Gia tốc hướng tâm luôn hướng vào tâm của quỹ đạo tròn.

Để hiểu rõ hơn về chuyển động tròn đều, việc xem xét các ví dụ thực tế và bài tập cụ thể là rất quan trọng. Dưới đây là một số ví dụ minh họa và bài tập giúp bạn vận dụng kiến thức đã học vào thực tế.

3.1. Ví dụ về chuyển động tròn đều

• Ví dụ 1: Chuyển động của kim đồng hồ - Kim giây của đồng hồ thực hiện một chuyển động tròn đều với chu kỳ 60 giây. Tốc độ góc của kim giây được tính bằng \(\omega = \frac{2\pi}{T}\), trong đó \(T = 60\) giây. Nhờ đó, ta có thể xác định được tốc độ dài của đầu kim đồng hồ.
• Ví dụ 2: Chuyển động của các hành tinh quanh mặt trời - Các hành tinh quay quanh mặt trời theo quỹ đạo gần tròn với tốc độ góc không đổi. Chuyển động của chúng là một ví dụ điển hình của chuyển động tròn đều trong vũ trụ.

3.2. Bài tập về chuyển động tròn đều

1. Bài tập 1: Tính tốc độ dài và gia tốc hướng tâm

   Một vật chuyển động tròn đều trên một quỹ đạo có bán kính \(r = 2\) m với tốc độ góc \(\omega = 5\) rad/s. Hãy tính tốc độ dài và gia tốc hướng tâm của vật.

   Lời giải:

   • Tốc độ dài: \( v = r\omega = 2 \times 5 = 10 \) m/s.
   • Gia tốc hướng tâm: \( a_{ht} = r\omega^2 = 2 \times 5^2 = 50 \) m/s².
2. Bài tập 2: Xác định chu kỳ quay

   Một vệ tinh nhân tạo quay quanh Trái Đất trên quỹ đạo tròn với bán kính \(r = 7000\) km và tốc độ dài \(v = 7.8\) km/s. Hãy tính chu kỳ quay của vệ tinh.

   Lời giải:

   • Tốc độ góc: \( \omega = \frac{v}{r} = \frac{7.8 \times 10^3}{7 \times 10^6} = 1.11 \times 10^{-3} \) rad/s.
   • Chu kỳ: \( T = \frac{2\pi}{\omega} = \frac{2\pi}{1.11 \times 10^{-3}} \approx 5650 \) giây.

3.3. Ứng dụng công thức vào các bài toán cụ thể

Bằng cách áp dụng các công thức tính toán đã học, chúng ta có thể giải quyết các bài toán thực tế liên quan đến chuyển động tròn đều, như tính toán vận tốc, chu kỳ, và gia tốc của các vật thể trong quỹ đạo tròn.

Chuyển động tròn đều không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng quan trọng trong thực tế. Những ứng dụng này không chỉ xuất hiện trong các hiện tượng tự nhiên mà còn được sử dụng rộng rãi trong kỹ thuật và công nghệ hiện đại.

• Ứng dụng trong thiên văn học:

  Trong thiên văn học, chuyển động tròn đều xuất hiện trong quỹ đạo của các hành tinh quanh mặt trời, các vệ tinh tự nhiên quanh hành tinh, và quỹ đạo của các vệ tinh nhân tạo quanh Trái Đất. Nhờ vào tính chất của chuyển động tròn đều, các nhà khoa học có thể dự đoán chính xác vị trí của các thiên thể trong tương lai.

• Ứng dụng trong kỹ thuật và công nghệ:

  Chuyển động tròn đều được ứng dụng trong nhiều thiết bị kỹ thuật như bánh xe, rôto trong động cơ điện, và các hệ thống truyền động. Ví dụ, trong động cơ điện, các rôto quay với tốc độ không đổi để đảm bảo hoạt động ổn định của thiết bị.

• Ứng dụng trong giao thông vận tải:

  Chuyển động tròn đều cũng được ứng dụng trong việc thiết kế đường cong trên các tuyến đường sắt và đường bộ. Để đảm bảo an toàn cho các phương tiện di chuyển, các đường cong này được thiết kế theo nguyên tắc của chuyển động tròn đều nhằm duy trì tốc độ ổn định và giảm thiểu rủi ro trượt.

• Ứng dụng trong cuộc sống hàng ngày:

  Trong cuộc sống hàng ngày, chuyển động tròn đều có thể được thấy ở các trò chơi như đu quay, bánh xe Ferris, và thậm chí là trong việc xoay chậu cây. Những ứng dụng này không chỉ giúp tạo ra sự ổn định mà còn mang lại trải nghiệm thú vị cho con người.

Để hiểu rõ hơn về chuyển động tròn đều và áp dụng kiến thức này vào thực tế, bạn có thể tham khảo một số tài liệu học tập và nguồn tài nguyên dưới đây. Những tài liệu này cung cấp từ kiến thức cơ bản đến nâng cao, giúp bạn củng cố và mở rộng hiểu biết về chủ đề này.

• Sách giáo khoa Vật lý 10:

  Sách giáo khoa Vật lý lớp 10 là nguồn tài liệu cơ bản và chính thống, cung cấp các kiến thức nền tảng về chuyển động tròn đều, bao gồm định nghĩa, công thức và các bài tập thực hành. Đây là tài liệu cần thiết cho học sinh trung học phổ thông.

• Bài giảng trực tuyến:

  Nhiều trang web giáo dục như ViettelStudy, HocMai.vn, và Olm.vn cung cấp các bài giảng trực tuyến và video hướng dẫn chi tiết về chuyển động tròn đều. Những bài giảng này thường được trình bày dễ hiểu, kèm theo ví dụ minh họa và bài tập thực hành.

• Tài liệu tham khảo:

  Các cuốn sách tham khảo như "Cơ học - Lý thuyết và bài tập" của tác giả Nguyễn Văn Khải và "Bài tập Vật lý chọn lọc" của tác giả Phạm Văn Bắc là những tài liệu hữu ích cho những ai muốn đào sâu hơn vào chủ đề chuyển động tròn đều, với nhiều bài tập đa dạng và phương pháp giải chi tiết.

• Website học tập:

  Một số website như Vndoc.com và Giaitoan.com cung cấp tài liệu học tập, bài tập trắc nghiệm và các dạng bài tập có lời giải chi tiết về chuyển động tròn đều. Đây là nguồn tài nguyên phong phú để ôn luyện và kiểm tra kiến thức.