Chủ đề một chất điểm m chuyển động tròn đều: Một chất điểm m chuyển động tròn đều là một khái niệm quan trọng trong vật lý học. Bài viết này sẽ cung cấp đầy đủ thông tin về định nghĩa, công thức tính toán, và ứng dụng thực tiễn của chuyển động tròn đều trong đời sống hàng ngày và kỹ thuật, giúp bạn hiểu rõ hơn về hiện tượng thú vị này.
Mục lục
Một Chất Điểm \(m\) Chuyển Động Tròn Đều
Chuyển động tròn đều là chuyển động của một chất điểm \(m\) theo quỹ đạo tròn với tốc độ không đổi. Đây là một khái niệm cơ bản trong vật lý học, thường được áp dụng để giải thích nhiều hiện tượng trong tự nhiên và kỹ thuật.
Các Đặc Điểm Của Chuyển Động Tròn Đều
- Tốc độ dài (\(v\)): Là tốc độ của chất điểm chuyển động dọc theo quỹ đạo tròn, được tính bằng \[v = \frac{s}{t}\], trong đó \(s\) là quãng đường đi được, và \(t\) là thời gian.
- Chu kỳ (\(T\)): Là thời gian để chất điểm thực hiện một vòng tròn hoàn chỉnh, được tính bằng \[T = \frac{2\pi R}{v}\], trong đó \(R\) là bán kính của quỹ đạo tròn.
- Tần số (\(f\)): Là số vòng quay mà chất điểm thực hiện trong một đơn vị thời gian, liên hệ với chu kỳ bởi công thức \[f = \frac{1}{T}\].
- Tốc độ góc (\(\omega\)): Là tốc độ thay đổi góc của bán kính quay, được tính bằng \[\omega = \frac{v}{R} = \frac{2\pi}{T}\].
- Gia tốc hướng tâm (\(a\)): Là gia tốc hướng vào tâm của quỹ đạo, cần thiết để duy trì chuyển động tròn đều, được tính bằng \[a = \frac{v^2}{R} = \omega^2 R\].
Công Thức Liên Quan
| Đại lượng | Công thức |
|---|---|
| Tốc độ dài (\(v\)) | \[v = \omega R\] |
| Chu kỳ (\(T\)) | \[T = \frac{2\pi}{\omega}\] |
| Tần số (\(f\)) | \[f = \frac{\omega}{2\pi}\] |
| Gia tốc hướng tâm (\(a\)) | \[a = \omega^2 R\] |
Ứng Dụng Thực Tiễn
Chuyển động tròn đều có nhiều ứng dụng trong thực tế, bao gồm:
- Thiết kế đường cong trên đường cao tốc: Đảm bảo xe cộ có thể di chuyển an toàn với tốc độ cao.
- Chuyển động của các hành tinh: Các hành tinh quay quanh Mặt Trời theo quỹ đạo gần tròn.
- Máy ly tâm: Sử dụng chuyển động tròn đều để tách các chất có khối lượng riêng khác nhau.
Kết Luận
Hiểu biết về chuyển động tròn đều không chỉ giúp chúng ta nắm bắt được các nguyên lý cơ bản của vật lý mà còn ứng dụng trong nhiều lĩnh vực của đời sống và công nghệ. Khái niệm này là nền tảng để phát triển thêm nhiều mô hình vật lý và kỹ thuật khác nhau, từ đó giải thích và khai thác các hiện tượng tự nhiên một cách hiệu quả.
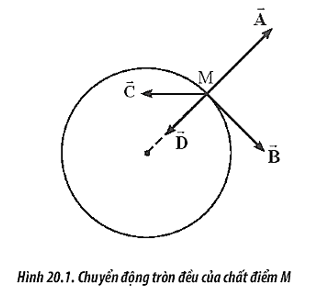
.png)
Khái Niệm Cơ Bản Về Chuyển Động Tròn Đều
Chuyển động tròn đều là một dạng chuyển động mà ở đó một chất điểm \(m\) di chuyển trên một quỹ đạo tròn với tốc độ góc không đổi. Đây là một trong những khái niệm cơ bản của cơ học cổ điển, giúp hiểu rõ hơn về các chuyển động có quỹ đạo cong trong không gian hai chiều.
- Quỹ đạo tròn: Chuyển động tròn đều xảy ra khi chất điểm di chuyển dọc theo một đường tròn cố định có bán kính \(R\). Quỹ đạo này có thể là một vòng tròn hoàn chỉnh hoặc một phần của nó.
- Tốc độ góc (\(\omega\)): Tốc độ góc là đại lượng mô tả mức độ thay đổi góc của bán kính nối từ tâm quỹ đạo đến chất điểm. Tốc độ góc trong chuyển động tròn đều là không đổi và được tính bằng công thức: \[ \omega = \frac{\Delta \theta}{\Delta t} \] trong đó \(\Delta \theta\) là góc quét được trong thời gian \(\Delta t\).
- Chu kỳ (\(T\)): Chu kỳ là thời gian cần thiết để chất điểm hoàn thành một vòng quay toàn phần trên quỹ đạo tròn. Chu kỳ liên quan đến tốc độ góc qua công thức: \[ T = \frac{2\pi}{\omega} \]
- Tần số (\(f\)): Tần số là số vòng quay mà chất điểm thực hiện được trong một đơn vị thời gian. Nó có mối quan hệ nghịch đảo với chu kỳ, được tính bởi: \[ f = \frac{1}{T} \]
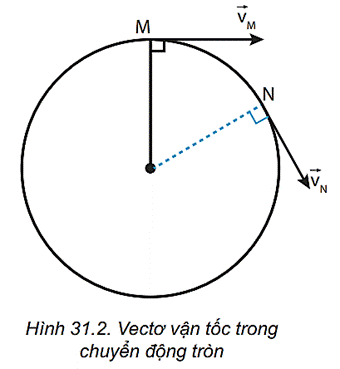
- Tốc độ dài (\(v\)): Tốc độ dài là tốc độ mà chất điểm di chuyển dọc theo quỹ đạo tròn. Nó có liên hệ với tốc độ góc và bán kính của quỹ đạo qua công thức: \[ v = \omega R \]
- Gia tốc hướng tâm (\(a\)): Gia tốc hướng tâm là gia tốc hướng vào tâm của quỹ đạo, luôn vuông góc với vận tốc của chất điểm. Đây là gia tốc cần thiết để duy trì chuyển động tròn đều, và được tính bởi: \[ a = \frac{v^2}{R} = \omega^2 R \]
Chuyển động tròn đều không chỉ là một khái niệm cơ bản trong vật lý mà còn có ứng dụng rộng rãi trong thực tế, từ các thiết bị quay trong công nghiệp đến chuyển động của các hành tinh trong thiên văn học. Việc hiểu rõ các đặc điểm và công thức liên quan đến chuyển động tròn đều giúp chúng ta giải thích nhiều hiện tượng tự nhiên và phát triển các công nghệ tiên tiến.
Công Thức và Phương Trình Liên Quan
Chuyển động tròn đều là chuyển động của một chất điểm trên một quỹ đạo tròn với tốc độ góc không đổi. Dưới đây là các công thức và phương trình liên quan đến chuyển động tròn đều:
Công Thức Tính Tốc Độ Dài
Tốc độ dài \(v\) của chất điểm được tính bằng công thức:
Trong đó:
- \(v\): Tốc độ dài (m/s)
- \(\omega\): Tốc độ góc (rad/s)
- \(R\): Bán kính quỹ đạo tròn (m)
Công Thức Tính Tốc Độ Góc
Tốc độ góc \(\omega\) là đại lượng biểu thị mức độ nhanh hay chậm của chuyển động quay quanh một trục và được tính bởi:
Trong đó:
- \(\omega\): Tốc độ góc (rad/s)
- \(T\): Chu kỳ chuyển động (s)
- \(f\): Tần số (Hz)
Công Thức Tính Chu Kỳ và Tần Số
Chu kỳ \(T\) là thời gian để chất điểm hoàn thành một vòng trên quỹ đạo, và tần số \(f\) là số vòng quay trong một đơn vị thời gian. Chúng có quan hệ với tốc độ góc như sau:
Công Thức Tính Gia Tốc Hướng Tâm và Lực Hướng Tâm
Gia tốc hướng tâm \(a_{ht}\) và lực hướng tâm \(F_{ht}\) giữ cho chất điểm luôn chuyển động trên quỹ đạo tròn đều:
Trong đó:
- \(a_{ht}\): Gia tốc hướng tâm (m/s²)
- \(F_{ht}\): Lực hướng tâm (N)
- \(m\): Khối lượng của chất điểm (kg)

Ứng Dụng Của Chuyển Động Tròn Đều Trong Thực Tế
Chuyển động tròn đều là một hiện tượng phổ biến trong nhiều lĩnh vực của cuộc sống hàng ngày và kỹ thuật. Dưới đây là một số ứng dụng điển hình của chuyển động tròn đều trong thực tế:
- Đồng hồ cơ: Một trong những ứng dụng phổ biến nhất của chuyển động tròn đều là trong các đồng hồ cơ. Kim phút và kim giờ của đồng hồ di chuyển với tốc độ góc không đổi, tạo ra một chuyển động tròn đều trên mặt số đồng hồ.
- Vệ tinh nhân tạo: Các vệ tinh quay quanh Trái Đất theo quỹ đạo gần như tròn. Chuyển động này có tốc độ góc không đổi, giúp vệ tinh duy trì vị trí của nó trong không gian để thực hiện các nhiệm vụ như truyền thông, dự báo thời tiết và giám sát.
- Bánh xe ô tô: Khi ô tô di chuyển, các bánh xe thực hiện chuyển động tròn đều, với mỗi điểm trên vành bánh xe di chuyển theo một quỹ đạo tròn quanh trục của bánh xe. Điều này giúp ô tô di chuyển mượt mà và ổn định.
- Máy gia tốc hạt: Trong các máy gia tốc hạt, như máy gia tốc electron, các hạt được tăng tốc theo quỹ đạo tròn đều với tốc độ rất cao. Điều này cho phép các nhà khoa học nghiên cứu cấu trúc của vật chất ở cấp độ nguyên tử và hạt nhân.
Như vậy, chuyển động tròn đều không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng thực tế quan trọng trong đời sống và công nghệ.

Bài Tập Về Chuyển Động Tròn Đều
Chuyển động tròn đều là một dạng chuyển động trong đó một chất điểm m di chuyển trên một quỹ đạo hình tròn với tốc độ góc không đổi. Dưới đây là một số bài tập điển hình về chuyển động tròn đều nhằm giúp bạn nắm vững các kiến thức cơ bản và áp dụng chúng vào giải quyết các bài toán thực tế.
-
Một lưỡi cưa tròn có đường kính 60 cm quay đều với chu kỳ là 0,2 s. Hãy xác định tốc độ góc và tốc độ dài của một điểm nằm trên vành ngoài lưỡi cưa.
- Giải:
- Tốc độ góc: \(\omega = 10 \, \text{rad/s}\)
- Tốc độ dài: \(v = \omega \cdot r = 9,42 \, \text{m/s}\)
-
Một chất điểm m chuyển động đều trên quỹ đạo tròn bán kính 40 cm. Biết trong một phút nó thực hiện được 300 vòng. Xác định tốc độ góc, tốc độ dài và gia tốc hướng tâm của chất điểm.
- Giải:
- Tốc độ góc: \(\omega = 31,42 \, \text{rad/s}\)
- Tốc độ dài: \(v = \omega \cdot r = 12,57 \, \text{m/s}\)
- Gia tốc hướng tâm: \(a_{ht} = \omega^2 \cdot r = 1577,92 \, \text{m/s}^2\)
-
Một ôtô có bánh xe bán kính 30 cm chuyển động đều với tốc độ 64,8 km/h. Hãy tính tốc độ góc, chu kỳ quay của bánh xe và gia tốc hướng tâm của một điểm trên vành ngoài bánh xe.
- Giải:
- Tốc độ góc: \(\omega = 60 \, \text{rad/s}\)
- Chu kỳ quay: \(T = 0,1 \, \text{s}\)
- Gia tốc hướng tâm: \(a_{ht} = 1080 \, \text{m/s}^2\)
-
Một đồng hồ treo tường có kim phút dài 12 cm và kim giờ dài 9 cm. Cho rằng các kim quay đều. Hãy tính tốc độ dài và tốc độ góc của điểm đầu hai kim.
- Giải:
- Tốc độ góc của kim giờ: \(\omega_{giờ} = \frac{2\pi}{43200} \, \text{rad/s}\)
- Tốc độ dài của điểm đầu kim giờ: \(v_{giờ} = \omega_{giờ} \cdot r_{giờ}\)
- Tốc độ góc của kim phút: \(\omega_{phút} = \frac{2\pi}{3600} \, \text{rad/s}\)
- Tốc độ dài của điểm đầu kim phút: \(v_{phút} = \omega_{phút} \cdot r_{phút}\)

Kết Luận và Ý Nghĩa Của Chuyển Động Tròn Đều
Chuyển động tròn đều là một hiện tượng cơ học quan trọng và có nhiều ứng dụng trong cuộc sống và khoa học. Kết quả nghiên cứu về chuyển động tròn đều giúp chúng ta hiểu rõ hơn về các lực tác động và sự cân bằng trong chuyển động quay, đồng thời là nền tảng cho nhiều ứng dụng kỹ thuật.
- Ổn định trong thiết kế kỹ thuật: Chuyển động tròn đều được áp dụng để thiết kế các hệ thống quay ổn định như trong động cơ điện, bánh xe, và các máy móc công nghiệp.
- Ứng dụng trong thiên văn học: Hiểu biết về chuyển động tròn đều giúp các nhà khoa học giải thích quỹ đạo của các hành tinh, vệ tinh và các thiên thể khác trong vũ trụ.
- Thiết kế hệ thống truyền động: Chuyển động tròn đều là nguyên lý cơ bản trong thiết kế hệ thống truyền động, giúp tối ưu hóa sự phân bố lực và chuyển động trong các cơ cấu máy móc.
Tóm lại, chuyển động tròn đều không chỉ là một phần kiến thức quan trọng trong cơ học mà còn có ý nghĩa thực tiễn sâu rộng, ứng dụng trong nhiều lĩnh vực từ kỹ thuật, công nghiệp đến nghiên cứu khoa học.

/https://static.texastribune.org/media/files/e8ca9aebefd8f17dfba4b788aa3a0493/2022Elections-leadart-vietnamese-v1.png)


















