Vectơ Vận Tốc Trong Chuyển Động Tròn Đều: Hiểu Rõ Từ A Đến Z

Chuyển động tròn đều là chuyển động mà vật thể di chuyển trên một quỹ đạo tròn với tốc độ không đổi. Trong loại chuyển động này, vectơ vận tốc đóng vai trò quan trọng trong việc mô tả hướng và độ lớn của vận tốc tại mỗi điểm trên quỹ đạo.

Đặc Điểm Của Vectơ Vận Tốc

• Độ lớn: Độ lớn của vectơ vận tốc trong chuyển động tròn đều là hằng số, nghĩa là tốc độ của vật không thay đổi trong suốt quá trình chuyển động. Công thức tính độ lớn của vận tốc là \(v = \omega \cdot r\), trong đó \(\omega\) là tốc độ góc và \(r\) là bán kính của quỹ đạo tròn.
• Hướng: Vectơ vận tốc luôn tiếp tuyến với quỹ đạo tròn tại mỗi điểm. Điều này có nghĩa là tại bất kỳ thời điểm nào, hướng của vận tốc sẽ vuông góc với bán kính kéo từ tâm quỹ đạo đến điểm đó.
• Sự thay đổi hướng: Mặc dù độ lớn của vectơ vận tốc không thay đổi, hướng của nó luôn thay đổi khi vật thể di chuyển trên quỹ đạo tròn. Đây là lý do vì sao trong chuyển động tròn đều, có gia tốc hướng tâm.

Gia Tốc Hướng Tâm

Gia tốc hướng tâm là gia tốc có phương luôn hướng vào tâm của quỹ đạo tròn và có độ lớn được tính theo công thức:

Trong đó:

• \(v\) là độ lớn của vận tốc.
• \(\omega\) là tốc độ góc.

Công Thức Liên Quan Đến Vectơ Vận Tốc

Các công thức quan trọng khác liên quan đến vectơ vận tốc trong chuyển động tròn đều bao gồm:

• Công thức tính tốc độ góc: \(\omega = \frac{v}{r}\).
• Công thức tính độ lớn của gia tốc hướng tâm: \[a_{\text{ht}} = \frac{v^2}{r}\] hoặc \[a_{\text{ht}} = \omega^2 \cdot r\].

Ứng Dụng Của Chuyển Động Tròn Đều

Chuyển động tròn đều và các khái niệm về vectơ vận tốc được ứng dụng rộng rãi trong nhiều lĩnh vực, từ kỹ thuật cơ khí, hàng không cho đến các nghiên cứu về động lực học vũ trụ. Hiểu rõ về vectơ vận tốc giúp chúng ta dễ dàng nắm bắt và điều khiển các quá trình liên quan đến chuyển động quay, từ bánh xe đến các hệ thống quay phức tạp.

Kết Luận

Vectơ vận tốc trong chuyển động tròn đều là một khái niệm cơ bản nhưng quan trọng trong vật lý, giúp chúng ta hiểu rõ hơn về cách thức vật thể di chuyển trong không gian. Nắm vững kiến thức này là bước đệm để tiếp cận các khái niệm phức tạp hơn trong động lực học và các ứng dụng thực tế.

Chuyển động tròn đều là một dạng chuyển động mà một vật thể di chuyển trên một quỹ đạo tròn với tốc độ không đổi. Trong chuyển động này, vận tốc của vật luôn có độ lớn không đổi nhưng hướng của nó liên tục thay đổi, luôn tiếp tuyến với quỹ đạo tròn.

Để mô tả chuyển động tròn đều, chúng ta cần xác định một số đại lượng đặc trưng:

• Chu kỳ \(T\): Là thời gian để vật thực hiện một vòng quay hoàn chỉnh, tính bằng giây (s).
• Tần số \(f\): Là số vòng quay mà vật thực hiện trong một đơn vị thời gian, tính bằng hertz (Hz). Công thức liên hệ giữa chu kỳ và tần số là \[f = \frac{1}{T}\].
• Bán kính quỹ đạo \(R\): Khoảng cách từ tâm của quỹ đạo đến điểm mà vật di chuyển trên quỹ đạo tròn, tính bằng mét (m).

Trong chuyển động tròn đều, vận tốc góc \(\omega\) cũng là một đại lượng quan trọng. Nó được định nghĩa là tốc độ thay đổi của góc quay theo thời gian, với công thức:

Vận tốc dài \(v\) của vật được liên hệ với vận tốc góc \(\omega\) và bán kính quỹ đạo \(R\) bởi công thức:

Do đó, vận tốc dài \(v\) không thay đổi về độ lớn nhưng liên tục thay đổi về hướng trong chuyển động tròn đều. Điều này dẫn đến sự xuất hiện của gia tốc hướng tâm, luôn hướng về tâm của quỹ đạo.

Trong chuyển động tròn đều, vectơ vận tốc là một đại lượng vector quan trọng giúp mô tả chính xác hướng và độ lớn của vận tốc tại mọi điểm trên quỹ đạo tròn. Đặc điểm của vectơ vận tốc trong chuyển động này bao gồm:

• Độ lớn không đổi: Vectơ vận tốc có độ lớn không đổi, được xác định bởi công thức \(v = \omega R\), trong đó \(v\) là vận tốc dài, \(\omega\) là vận tốc góc, và \(R\) là bán kính quỹ đạo.
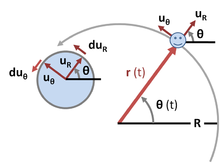
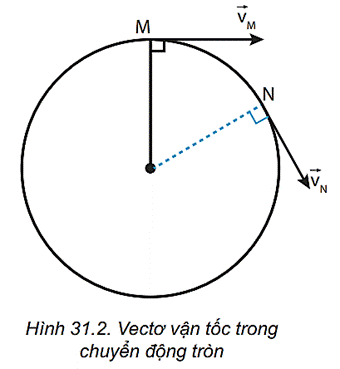
• Hướng thay đổi liên tục: Mặc dù độ lớn của vectơ vận tốc không thay đổi, nhưng hướng của nó luôn thay đổi để tiếp tuyến với quỹ đạo tròn tại mỗi điểm. Hướng của vectơ vận tốc tạo với bán kính của quỹ đạo một góc \(90^\circ\).

Để hiểu rõ hơn, hãy xem xét một vật thể đang di chuyển trên quỹ đạo tròn. Tại mỗi điểm trên quỹ đạo, vectơ vận tốc luôn vuông góc với bán kính nối từ tâm đến điểm đó. Điều này có nghĩa là khi vật thể di chuyển, hướng của vectơ vận tốc thay đổi liên tục, nhưng độ lớn thì vẫn giữ nguyên.

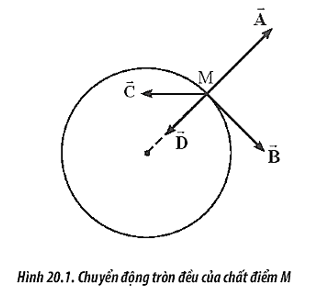
Giả sử vật thể di chuyển từ điểm \(A\) đến điểm \(B\) trên quỹ đạo tròn, vectơ vận tốc tại điểm \(A\) sẽ là \(\vec{v}_A\) và tại điểm \(B\) sẽ là \(\vec{v}_B\). Do hướng của vectơ vận tốc thay đổi, sự chênh lệch giữa hai vectơ này tạo ra một vectơ gia tốc hướng tâm \(\vec{a}_h\) luôn hướng về tâm của quỹ đạo, giúp giữ cho vật thể di chuyển trên quỹ đạo tròn đều.

Gia tốc hướng tâm có thể được tính theo công thức:

Gia tốc này không làm thay đổi độ lớn của vận tốc mà chỉ thay đổi hướng của nó, giúp vật thể duy trì chuyển động trên quỹ đạo tròn đều.

Gia tốc hướng tâm là một yếu tố quan trọng trong chuyển động tròn đều, giúp duy trì quỹ đạo tròn của vật thể. Gia tốc này luôn hướng về tâm của quỹ đạo và giữ cho vật thể di chuyển liên tục theo đường tròn.

Gia tốc hướng tâm được xác định bởi công thức:

Trong đó:

• \(a_h\) là gia tốc hướng tâm.
• \(v\) là vận tốc dài của vật thể.
• \(\omega\) là vận tốc góc.
• \(R\) là bán kính quỹ đạo.

Gia tốc hướng tâm không thay đổi độ lớn của vận tốc nhưng liên tục thay đổi hướng của nó, tạo điều kiện cho vật thể duy trì chuyển động tròn đều. Điều này có nghĩa là mặc dù vận tốc của vật thể có hướng thay đổi nhưng độ lớn của nó vẫn không đổi, nhờ vậy mà vật thể tiếp tục di chuyển trên quỹ đạo tròn.

Để dễ hiểu hơn, hãy tưởng tượng một vật thể đang quay quanh một điểm cố định. Nếu không có gia tốc hướng tâm, vật thể sẽ di chuyển theo đường thẳng do quán tính. Tuy nhiên, nhờ vào lực hướng tâm tác động, vật thể liên tục bị "kéo" vào tâm, tạo nên chuyển động tròn đều.

Như vậy, gia tốc hướng tâm đóng vai trò quan trọng trong việc duy trì quỹ đạo tròn đều của vật thể, đảm bảo rằng vật thể không bị văng ra khỏi quỹ đạo và tiếp tục chuyển động ổn định.

Vectơ vận tốc trong chuyển động tròn đều có nhiều ứng dụng quan trọng trong thực tế, từ các hiện tượng tự nhiên đến công nghệ hiện đại. Những ứng dụng này không chỉ giúp chúng ta hiểu rõ hơn về các nguyên lý vật lý mà còn cải thiện nhiều khía cạnh của cuộc sống.

Một số ứng dụng thực tế của vectơ vận tốc trong chuyển động tròn đều bao gồm:

• Hệ thống vệ tinh: Các vệ tinh nhân tạo quay quanh Trái Đất theo quỹ đạo tròn đều. Vectơ vận tốc trong trường hợp này giúp duy trì quỹ đạo ổn định, cho phép vệ tinh cung cấp thông tin liên lạc và dự báo thời tiết.
• Máy ly tâm: Trong công nghệ y tế và nghiên cứu, máy ly tâm sử dụng chuyển động tròn đều để tách các thành phần trong mẫu dựa trên khối lượng và mật độ. Vectơ vận tốc giúp tạo lực ly tâm cần thiết để thực hiện quá trình này.
• Các hệ thống quay trong công nghiệp: Các máy móc như tuabin gió, động cơ ô tô, và các hệ thống băng chuyền thường sử dụng chuyển động tròn đều. Vectơ vận tốc giúp tính toán và kiểm soát tốc độ quay, đảm bảo hiệu suất cao và an toàn.
• Các trò chơi và thể thao: Trong các trò chơi như quay vòng, vectơ vận tốc giúp người chơi nắm bắt được tốc độ và hướng di chuyển, tạo cảm giác phấn khích và an toàn.

Những ứng dụng này cho thấy rằng vectơ vận tốc trong chuyển động tròn đều không chỉ là một khái niệm lý thuyết mà còn có giá trị thực tiễn lớn, đóng góp vào nhiều lĩnh vực khác nhau trong cuộc sống.

Dưới đây là một số bài tập thực hành liên quan đến vectơ vận tốc trong chuyển động tròn đều, giúp bạn củng cố kiến thức và hiểu rõ hơn về chủ đề này.

Bài Tập 1: Tính Vận Tốc Góc và Vận Tốc Dài

Một vật thể đang chuyển động tròn đều với bán kính quỹ đạo là \( r = 50 \, \text{cm} \). Vật thể hoàn thành 1 vòng quay trong 4 giây. Hãy tính:

1. Vận tốc góc \( \omega \) của vật thể.
2. Vận tốc dài \( v \) của vật thể.

Giải:

1. Vận tốc góc \( \omega \) được tính bằng công thức: \[ \omega = \frac{2\pi}{T} \] Trong đó, \( T = 4 \, \text{giây} \), vậy: \[ \omega = \frac{2\pi}{4} = \frac{\pi}{2} \, \text{rad/s} \]
2. Vận tốc dài \( v \) được tính bằng công thức: \[ v = r \cdot \omega \] Với \( r = 0,5 \, \text{m} \) và \( \omega = \frac{\pi}{2} \, \text{rad/s} \), ta có: \[ v = 0,5 \times \frac{\pi}{2} = \frac{\pi}{4} \, \text{m/s} \]

Bài Tập 2: Tính Gia Tốc Hướng Tâm

Một đĩa tròn đang quay đều với vận tốc góc \( \omega = 10 \, \text{rad/s} \). Biết rằng bán kính của đĩa là \( r = 20 \, \text{cm} \). Tính gia tốc hướng tâm của một điểm trên vành đĩa.

Giải:

Gia tốc hướng tâm \( a_{\text{ht}} \) được tính bằng công thức:

Với \( \omega = 10 \, \text{rad/s} \) và \( r = 0,2 \, \text{m} \), ta có:

Bài Tập 3: Vận Tốc Tại Các Điểm Khác Nhau

Một vệ tinh đang quay tròn quanh Trái Đất theo quỹ đạo cách bề mặt 400 km. Biết thời gian vệ tinh hoàn thành 1 vòng là 90 phút. Hãy tính tốc độ góc và vận tốc của vệ tinh.

Giải:

1. Tốc độ góc \( \omega \) được tính bằng công thức: \[ \omega = \frac{2\pi}{T} \] Với \( T = 5400 \, \text{giây} \), ta có: \[ \omega = \frac{2\pi}{5400} = 1,16 \times 10^{-3} \, \text{rad/s} \]
2. Vận tốc \( v \) của vệ tinh được tính bằng công thức: \[ v = r \cdot \omega \] Với bán kính quỹ đạo \( r = 6789 \, \text{km} \), ta có: \[ v = 6789 \times 1,16 \times 10^{-3} = 7,88 \, \text{km/s} \]