Một Vật Chuyển Động Tròn Đều Với Bán Kính r: Khám Phá Cơ Chế Hoạt Động Và Ứng Dụng

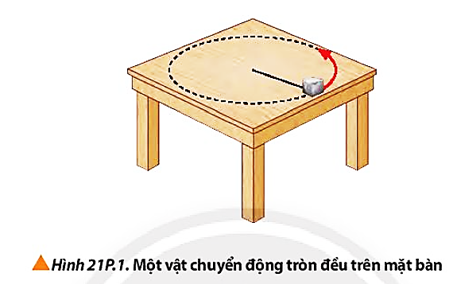
Một vật chuyển động tròn đều là chuyển động của một vật trên một quỹ đạo tròn với tốc độ góc không đổi. Trong đó, bán kính \( r \) là khoảng cách từ vật đến tâm của quỹ đạo. Đây là một dạng chuyển động cơ bản trong vật lý, thường được đề cập trong các chương trình giáo dục phổ thông.

Các Đại Lượng Liên Quan Đến Chuyển Động Tròn Đều

• Tốc độ góc \(\omega\): Là đại lượng đặc trưng cho mức độ nhanh chậm của chuyển động tròn, được tính bằng công thức: \[ \omega = \frac{v}{r} \] trong đó \(v\) là tốc độ dài của vật, và \(r\) là bán kính quỹ đạo.
• Gia tốc hướng tâm \(a_{ht}\): Là gia tốc của vật có phương hướng vào tâm quỹ đạo, được tính theo công thức: \[ a_{ht} = \omega^2 r = \frac{v^2}{r} \] Gia tốc này luôn vuông góc với vận tốc và có độ lớn không đổi.
• Chu kỳ \(T\): Là khoảng thời gian để vật đi hết một vòng trên quỹ đạo, được xác định bởi công thức: \[ T = \frac{2\pi r}{v} = \frac{2\pi}{\omega} \]
• Tần số \(f\): Là số vòng mà vật đi được trong một đơn vị thời gian, liên hệ với chu kỳ qua công thức: \[ f = \frac{1}{T} \]

Ví Dụ Minh Họa

Xét một vật chuyển động tròn đều với tốc độ góc \( \omega = 2 \, \text{rad/s} \) và bán kính quỹ đạo \( r = 0.5 \, \text{m} \). Khi đó:

• Tốc độ dài của vật là: \[ v = \omega \times r = 2 \times 0.5 = 1 \, \text{m/s} \]
• Gia tốc hướng tâm là: \[ a_{ht} = \omega^2 \times r = 2^2 \times 0.5 = 2 \, \text{m/s}^2 \]
• Chu kỳ của vật là: \[ T = \frac{2\pi}{\omega} = \frac{2\pi}{2} = \pi \, \text{s} \]
• Tần số của vật là: \[ f = \frac{1}{T} = \frac{1}{\pi} \, \text{Hz} \]

Kết Luận

Chuyển động tròn đều là một trong những khái niệm cơ bản trong vật lý, giúp học sinh hiểu rõ hơn về các đại lượng như tốc độ góc, gia tốc hướng tâm, chu kỳ và tần số. Việc nắm vững các công thức và hiểu cách áp dụng chúng vào các bài toán thực tế là rất quan trọng trong quá trình học tập và nghiên cứu.

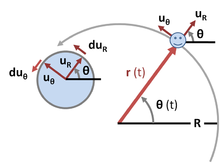
Chuyển động tròn đều là một loại chuyển động mà một vật di chuyển theo quỹ đạo tròn với tốc độ góc \(\omega\) không đổi. Trong quá trình này, vật luôn duy trì khoảng cách không đổi so với tâm quỹ đạo, được xác định bằng bán kính \(r\).

Để hiểu rõ hơn về chuyển động tròn đều, ta cần chú ý đến một số yếu tố quan trọng:

• Quỹ đạo tròn: Đây là đường cong mà vật di chuyển theo, có hình dạng là một đường tròn với bán kính \(r\). Quỹ đạo này có thể nằm trong mặt phẳng ngang hoặc nghiêng tùy vào điều kiện cụ thể.
• Tốc độ góc \(\omega\): Là đại lượng đặc trưng cho tốc độ quay của vật quanh tâm quỹ đạo. Nó được tính bằng công thức: \[ \omega = \frac{\Delta \theta}{\Delta t} \] trong đó \(\Delta \theta\) là góc quét được trong khoảng thời gian \(\Delta t\).
• Tốc độ dài \(v\): Là tốc độ di chuyển của vật trên quỹ đạo tròn, được tính theo công thức: \[ v = \omega \times r \] Tốc độ dài này là không đổi trong chuyển động tròn đều.
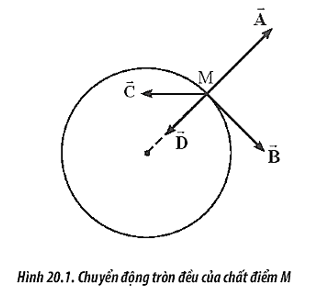
• Gia tốc hướng tâm \(a_{ht}\): Là gia tốc có phương luôn hướng vào tâm của quỹ đạo, giữ cho vật di chuyển theo đường tròn. Gia tốc này có độ lớn được tính bởi: \[ a_{ht} = \frac{v^2}{r} = \omega^2 \times r \]

Chuyển động tròn đều là một trong những chuyển động cơ bản và quan trọng trong vật lý, giúp ta hiểu rõ hơn về các nguyên lý động lực học và cách chúng áp dụng trong thực tế, từ chuyển động của các hành tinh quanh Mặt Trời đến hoạt động của các thiết bị cơ học hàng ngày.

Chuyển động tròn đều là một trong những khái niệm cơ bản trong vật lý, với nhiều công thức quan trọng giúp chúng ta mô tả và tính toán các đặc tính của chuyển động này. Dưới đây là các công thức tính toán quan trọng liên quan đến chuyển động tròn đều:

• Công thức tính tốc độ góc \(\omega\):

  Tốc độ góc \(\omega\) là đại lượng thể hiện mức độ nhanh hay chậm của sự quay quanh tâm quỹ đạo và được tính bằng:

  \[ \omega = \frac{\Delta \theta}{\Delta t} \]

  Trong đó, \(\Delta \theta\) là góc quét được trong khoảng thời gian \(\Delta t\).

• Công thức tính tốc độ dài \(v\):

  Tốc độ dài là tốc độ di chuyển của vật theo quỹ đạo tròn, liên hệ với tốc độ góc qua công thức:

  \[ v = \omega \times r \]

  Trong đó, \(r\) là bán kính của quỹ đạo.

• Công thức tính gia tốc hướng tâm \(a_{ht}\):

  Gia tốc hướng tâm là gia tốc cần thiết để duy trì chuyển động tròn đều của vật, được tính bằng:

  \[ a_{ht} = \frac{v^2}{r} = \omega^2 \times r \]

  Gia tốc này có phương hướng vào tâm của quỹ đạo tròn.

• Công thức tính chu kỳ \(T\):

  Chu kỳ là khoảng thời gian để vật di chuyển hết một vòng quỹ đạo, được xác định bởi công thức:

  \[ T = \frac{2\pi}{\omega} \]

  Chu kỳ cho biết thời gian cần thiết để vật hoàn thành một vòng quay.

• Công thức tính tần số \(f\):

  Tần số là số lần vật quay được trong một đơn vị thời gian, liên hệ với chu kỳ qua công thức:

  \[ f = \frac{1}{T} = \frac{\omega}{2\pi} \]

Những công thức này không chỉ giúp ta hiểu rõ hơn về các khía cạnh của chuyển động tròn đều mà còn là cơ sở để giải quyết các bài toán phức tạp hơn trong vật lý và kỹ thuật.

Để giúp bạn hiểu rõ hơn về chuyển động tròn đều, dưới đây là một số ví dụ minh họa cụ thể, kèm theo các bước tính toán chi tiết:

Ví dụ 1: Tính Tốc Độ Dài

Giả sử một vật chuyển động tròn đều với bán kính \(r = 2 \, \text{m}\) và có tốc độ góc \(\omega = 3 \, \text{rad/s}\). Tính tốc độ dài của vật.

Giải: Sử dụng công thức tính tốc độ dài:

Thay các giá trị vào, ta có:

Vậy tốc độ dài của vật là \(6 \, \text{m/s}\).

Ví dụ 2: Tính Gia Tốc Hướng Tâm

Một xe đạp đang di chuyển trên một đường tròn với bán kính \(r = 10 \, \text{m}\) và tốc độ dài \(v = 5 \, \text{m/s}\). Tính gia tốc hướng tâm của xe đạp.

Giải: Sử dụng công thức tính gia tốc hướng tâm:

Thay các giá trị vào, ta có:

Vậy gia tốc hướng tâm của xe đạp là \(2.5 \, \text{m/s}^2\).

Ví dụ 3: Ứng Dụng Công Thức Chu Kỳ và Tần Số

Một hành tinh quay quanh Mặt Trời theo quỹ đạo tròn với tốc độ góc \(\omega = 0.01 \, \text{rad/s}\). Tính chu kỳ và tần số của hành tinh này.

Giải:

• Tính chu kỳ \(T\):
\[ T = \frac{2\pi}{\omega} = \frac{2\pi}{0.01 \, \text{rad/s}} = 628.32 \, \text{s} \]
• Tính tần số \(f\):
\[ f = \frac{1}{T} = \frac{1}{628.32 \, \text{s}} \approx 0.0016 \, \text{Hz} \]

Vậy chu kỳ của hành tinh là \(628.32 \, \text{s}\) và tần số là \(0.0016 \, \text{Hz}\).

Chuyển động tròn đều là một chủ đề cơ bản trong vật lý, đặc biệt quan trọng khi nghiên cứu các hệ thống quay và các vật thể di chuyển theo quỹ đạo tròn. Dưới đây là tổng kết các kiến thức cơ bản về chuyển động tròn đều:

• Khái niệm cơ bản: Chuyển động tròn đều là chuyển động của một vật trên quỹ đạo tròn với tốc độ không đổi. Trong loại chuyển động này, vật di chuyển với một tốc độ góc \(\omega\) và giữ một bán kính \(r\) không đổi.
• Các đại lượng chính:
  • Tốc độ góc \(\omega\): Được đo bằng radian trên giây (rad/s), là đại lượng biểu thị tốc độ quay của vật quanh trục của nó.
  • Tốc độ dài \(v\): Biểu thị tốc độ di chuyển của vật dọc theo quỹ đạo tròn, tính theo công thức \(v = \omega \times r\).
  • Gia tốc hướng tâm \(a_{ht}\): Gia tốc có phương hướng vào tâm quỹ đạo, giữ cho vật không bị văng ra ngoài, với công thức \(a_{ht} = \frac{v^2}{r} = \omega^2 \times r\).
  • Chu kỳ \(T\): Là thời gian để vật đi hết một vòng quanh quỹ đạo, được tính theo công thức \(T = \frac{2\pi}{\omega}\).
  • Tần số \(f\): Là số vòng quay mà vật thực hiện được trong một đơn vị thời gian, tính theo công thức \(f = \frac{1}{T} = \frac{\omega}{2\pi}\).
• Ứng dụng thực tế: Chuyển động tròn đều có ứng dụng rộng rãi trong nhiều lĩnh vực như thiên văn học (quỹ đạo của các hành tinh), cơ học (chuyển động của bánh xe), và kỹ thuật (các bộ phận quay trong máy móc).

Việc hiểu rõ các công thức và nguyên lý của chuyển động tròn đều không chỉ giúp nắm vững các kiến thức vật lý cơ bản mà còn có thể áp dụng vào việc giải quyết các bài toán thực tế một cách hiệu quả.