Dao Động Điều Hòa và Chuyển Động Tròn Đều: Khám Phá Đặc Điểm và Ứng Dụng Thực Tế

Dao động điều hòa là một trong những kiến thức quan trọng trong môn Vật lý, liên quan đến các hiện tượng tự nhiên mà chúng ta thường gặp trong cuộc sống hàng ngày. Nó mô tả sự dao động qua lại của một vật quanh vị trí cân bằng dưới tác động của lực phục hồi. Chuyển động tròn đều là một dạng chuyển động trong đó vật thể di chuyển trên một đường tròn với tốc độ không đổi. Hai khái niệm này có mối liên hệ mật thiết với nhau.

1. Mối Quan Hệ Giữa Dao Động Điều Hòa và Chuyển Động Tròn Đều

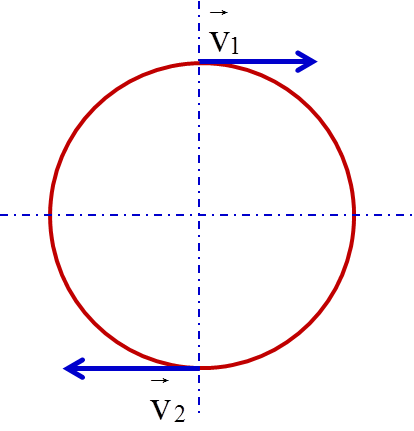
Dao động điều hòa có thể được biểu diễn bằng chuyển động tròn đều nếu ta tưởng tượng một điểm trên đường tròn có bán kính bằng biên độ dao động. Khi điểm đó di chuyển trên đường tròn với tốc độ góc không đổi, hình chiếu của nó trên một trục sẽ thực hiện dao động điều hòa.

Các phương trình liên quan giữa dao động điều hòa và chuyển động tròn đều có thể được biểu diễn bằng các công thức toán học như sau:

• Phương trình dao động điều hòa: \[x = A \cos(\omega t + \varphi)\]
• Phương trình chuyển động tròn đều: \[x = A \cos(\omega t)\] và \[y = A \sin(\omega t)\]
• Liên hệ giữa tốc độ góc \(\omega\) của chuyển động tròn và tần số dao động: \(\omega = 2\pi f\)

2. Tính Chất của Dao Động Điều Hòa

• Biên độ \(A\): Là giá trị lớn nhất mà vật đạt được khi dao động.
• Tần số góc \(\omega\): Là tốc độ góc trong chuyển động tròn đều, được tính bằng \(\omega = 2\pi f\).
• Chu kỳ \(T\): Là thời gian để vật hoàn thành một dao động toàn phần, được tính bằng \(T = \frac{2\pi}{\omega}\).
• Pha ban đầu \(\varphi\): Quyết định vị trí ban đầu của vật tại thời điểm \(t = 0\).

3. Ứng Dụng của Dao Động Điều Hòa và Chuyển Động Tròn Đều

Dao động điều hòa và chuyển động tròn đều không chỉ là kiến thức cơ bản trong vật lý, mà còn có nhiều ứng dụng thực tiễn:

• Trong các thiết bị cơ học như đồng hồ, máy phát điện, và động cơ điện.
• Trong nghiên cứu sóng và âm thanh, dao động điều hòa giúp giải thích các hiện tượng như sóng dừng, sóng âm và âm nhạc.
• Chuyển động tròn đều được sử dụng trong các hệ thống bánh răng, trục và vòng quay.

4. Bài Toán Minh Họa

Hãy xem xét một ví dụ minh họa để hiểu rõ hơn về dao động điều hòa:

Giả sử một chất điểm dao động điều hòa quanh vị trí cân bằng với biên độ \(A = 5cm\) và tần số góc \(\omega = 2\pi rad/s\). Khi đó, phương trình dao động có thể viết là:

\[x(t) = 5 \cos(2\pi t + \varphi)\]

Để tính thời gian ngắn nhất mà chất điểm đi từ vị trí \(x_1 = 3cm\) đến \(x_2 = -3cm\), ta sử dụng phương trình:

\[t = \frac{1}{\omega} \cos^{-1}\left(\frac{x_1}{A}\right) - \cos^{-1}\left(\frac{x_2}{A}\right)\]

Kết quả tính toán cho thấy thời gian ngắn nhất là 0.5 giây.

5. Kết Luận

Hiểu biết về dao động điều hòa và chuyển động tròn đều giúp chúng ta nắm bắt được các hiện tượng tự nhiên xung quanh và ứng dụng chúng vào đời sống thực tiễn. Từ đồng hồ, máy móc, cho đến các ứng dụng khoa học kỹ thuật cao, kiến thức này luôn đóng vai trò quan trọng.

Dao động điều hòa là một dạng dao động mà trong đó một vật di chuyển qua lại quanh một vị trí cân bằng theo quy luật hình sin hoặc cosin. Phương trình cơ bản của dao động điều hòa có dạng:

• \(x = A \cos(\omega t + \varphi)\)
• Trong đó:
  • \(x\) là li độ (vị trí của vật tại thời điểm \(t\))
  • \(A\) là biên độ (độ lớn cực đại của dao động)
  • \(\omega\) là tần số góc (đại lượng đặc trưng cho tốc độ dao động)
  • \(\varphi\) là pha ban đầu

Chuyển động tròn đều là chuyển động của một vật trên một quỹ đạo tròn với tốc độ không đổi. Để liên hệ giữa dao động điều hòa và chuyển động tròn đều, ta có thể coi dao động điều hòa như hình chiếu của chuyển động tròn đều lên một trục trong mặt phẳng dao động. Điều này cho phép dễ dàng liên hệ các đại lượng trong dao động điều hòa với các đại lượng trong chuyển động tròn đều.

• Biên độ \(A\) tương ứng với bán kính quỹ đạo tròn \(R\)
• Tần số góc \(\omega\) của dao động tương ứng với tốc độ góc của chuyển động tròn đều

Qua đó, ta thấy được sự tương đồng giữa hai loại chuyển động này, giúp đơn giản hóa các bài toán liên quan đến dao động và chuyển động tròn.

Trong dao động điều hòa, phương trình toán học đóng vai trò quan trọng trong việc mô tả chính xác chuyển động của vật theo thời gian. Phương trình này có thể được biểu diễn dưới dạng:

Trong đó:

• \(x\) là li độ của vật tại thời điểm \(t\), thể hiện vị trí của vật so với vị trí cân bằng.
• \(A\) là biên độ dao động, giá trị lớn nhất mà li độ \(x\) có thể đạt được.
• \(\omega\) là tần số góc, xác định tốc độ dao động của vật, được tính theo công thức \(\omega = \frac{2\pi}{T}\) với \(T\) là chu kỳ dao động.
• \(\varphi\) là pha ban đầu của dao động, xác định vị trí ban đầu của vật tại thời điểm \(t = 0\).

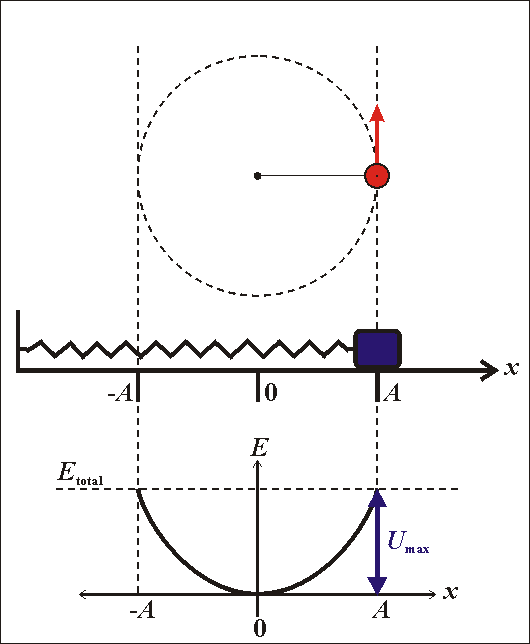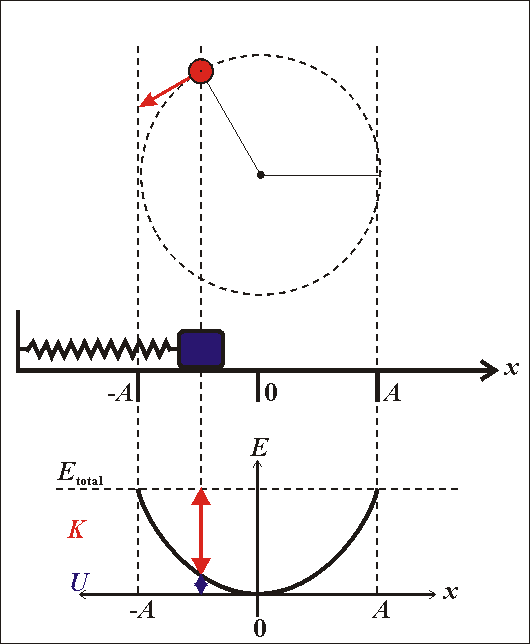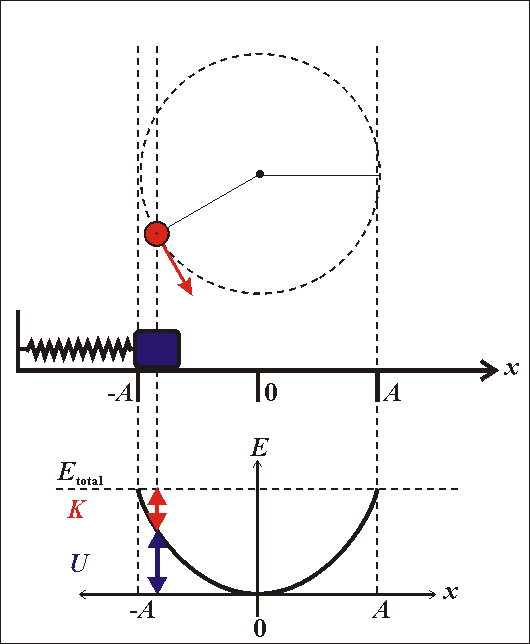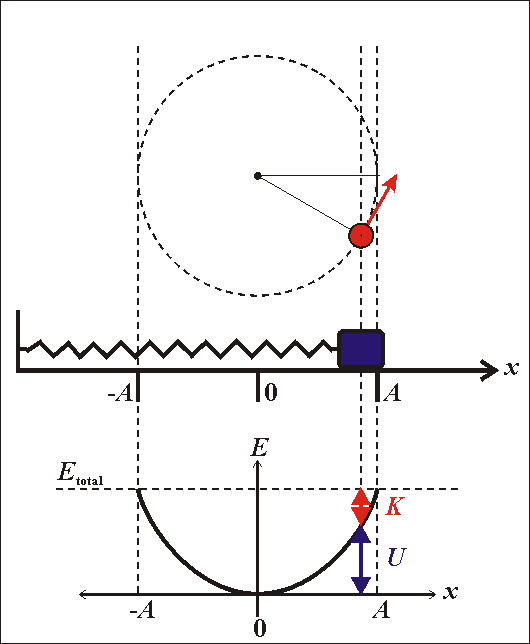
Phương trình này cho thấy dao động điều hòa có thể được xem như hình chiếu của chuyển động tròn đều lên một trục nằm trong mặt phẳng quỹ đạo. Cụ thể, nếu ta xét một điểm \(M\) chuyển động tròn đều với tốc độ góc \(\omega\), hình chiếu của \(M\) lên trục \(Ox\) sẽ tạo ra dao động điều hòa với phương trình trên.

Về mặt toán học, có thể biểu diễn phương trình này dưới dạng sin thay vì cos, tùy thuộc vào cách chọn gốc thời gian:

Cả hai dạng đều mô tả cùng một loại dao động, chỉ khác nhau ở cách chọn pha ban đầu. Đặc điểm nổi bật của dao động điều hòa là sự tuần hoàn và đối xứng, được mô tả chính xác qua các phương trình toán học này.

Điều quan trọng cần lưu ý là pha dao động \(\omega t + \varphi\) sẽ quyết định trạng thái tức thời của vật, và giá trị pha này cũng liên quan chặt chẽ đến hình chiếu của điểm trong chuyển động tròn đều.

Trong vật lý, dao động điều hòa và chuyển động tròn đều là hai khái niệm có mối quan hệ mật thiết với nhau. Các đặc điểm và tính chất của chúng có thể được phân tích chi tiết như sau:

• Đặc Điểm của Dao Động Điều Hòa:
  • Dao động điều hòa là chuyển động lặp đi lặp lại quanh một vị trí cân bằng, trong đó lực hồi phục luôn hướng về vị trí cân bằng và tỷ lệ thuận với độ lệch so với vị trí đó.
  • Biên độ dao động là khoảng cách lớn nhất từ vị trí cân bằng đến vị trí xa nhất mà vật đạt được.
  • Chu kỳ \(T\) là khoảng thời gian để vật thực hiện một dao động toàn phần, và tần số \(f\) là số dao động toàn phần thực hiện trong một đơn vị thời gian, với \(f = \frac{1}{T}\).
  • Vận tốc và gia tốc của vật dao động điều hòa luôn biến đổi theo thời gian và đạt giá trị cực đại tại vị trí cân bằng.
• Tính Chất của Chuyển Động Tròn Đều:
  • Chuyển động tròn đều là chuyển động của một vật trên một đường tròn với tốc độ không đổi, nhưng hướng của vận tốc thay đổi liên tục.
  • Trong chuyển động tròn đều, gia tốc hướng tâm \(a_t\) luôn hướng vào tâm của quỹ đạo và có độ lớn \(a_t = \frac{v^2}{R}\), với \(v\) là vận tốc của vật và \(R\) là bán kính của đường tròn.
  • Thời gian để vật hoàn thành một vòng quay chính là chu kỳ \(T\) của chuyển động tròn đều, được tính bằng \(T = \frac{2\pi R}{v}\).
• Mối Quan Hệ Giữa Dao Động Điều Hòa và Chuyển Động Tròn Đều:
  • Một điểm dao động điều hòa có thể được xem là hình chiếu của một điểm chuyển động tròn đều lên một đường thẳng cố định. Vì vậy, mọi tính chất của dao động điều hòa có thể được giải thích thông qua chuyển động tròn đều.
  • Tần số góc của dao động điều hòa bằng với tốc độ góc của chuyển động tròn đều, ký hiệu là \(\omega\).
  • Vị trí, vận tốc, và gia tốc của vật dao động điều hòa tương ứng với các thành phần theo trục tọa độ của vị trí, vận tốc, và gia tốc trong chuyển động tròn đều.

Những đặc điểm và tính chất này giúp chúng ta hiểu rõ hơn về bản chất của dao động điều hòa thông qua mối quan hệ chặt chẽ với chuyển động tròn đều, từ đó áp dụng vào nhiều lĩnh vực trong vật lý và kỹ thuật.

Dao động điều hòa và chuyển động tròn đều là hai hiện tượng vật lý có mối liên hệ chặt chẽ và được ứng dụng rộng rãi trong nhiều lĩnh vực của cuộc sống. Dưới đây là một số ứng dụng tiêu biểu:

• Đồng hồ quả lắc: Nguyên lý hoạt động của đồng hồ quả lắc dựa trên dao động điều hòa. Chuyển động tròn đều của quả lắc tạo ra dao động điều hòa, giúp đo thời gian chính xác.
• Máy phát điện xoay chiều: Chuyển động quay của cuộn dây trong từ trường là một ví dụ của chuyển động tròn đều. Dao động điều hòa của dòng điện được tạo ra khi cuộn dây cắt qua các đường sức từ, dẫn đến việc phát điện xoay chiều.
• Hệ thống treo trong xe hơi: Các bộ phận treo của xe hoạt động dựa trên dao động điều hòa để hấp thụ chấn động từ mặt đường, giúp xe di chuyển êm ái hơn.
• Kỹ thuật điều khiển: Trong các hệ thống điều khiển tự động, việc sử dụng dao động điều hòa giúp ổn định và điều chỉnh các biến đổi của hệ thống, như trong các bộ điều khiển PID.
• Thiết kế cầu và tòa nhà: Dao động điều hòa được tính toán để đảm bảo các công trình chịu được tải trọng và dao động từ gió, động đất, và các yếu tố ngoại cảnh khác, từ đó giúp nâng cao độ an toàn và độ bền.

Như vậy, ứng dụng của dao động điều hòa và chuyển động tròn đều rất đa dạng, từ các thiết bị hàng ngày như đồng hồ, đến những hệ thống phức tạp như máy phát điện và các công trình xây dựng. Hiểu rõ nguyên lý hoạt động của chúng giúp tối ưu hóa hiệu suất và an toàn trong các ứng dụng thực tế.

Để nắm vững hơn về mối quan hệ giữa dao động điều hòa và chuyển động tròn đều, việc thực hành thông qua các bài tập là rất quan trọng. Dưới đây là một số bài tập mẫu cùng với hướng dẫn giải:

1. Bài tập 1: Một vật dao động điều hòa có phương trình \(x(t) = A\cos(\omega t + \varphi)\). Xác định vị trí và vận tốc của vật tại thời điểm \(t = t_0\).

   Hướng dẫn:

   • Xác định các giá trị \(A\), \(\omega\), và \(\varphi\) từ đề bài.
   • Sử dụng phương trình \(x(t) = A\cos(\omega t + \varphi)\) để tìm vị trí \(x(t_0)\).
   • Vận tốc được tính bằng đạo hàm của phương trình dao động: \(v(t) = -A\omega\sin(\omega t + \varphi)\). Thay \(t = t_0\) để tìm vận tốc tại thời điểm này.

2. Bài tập 2: Một chất điểm chuyển động tròn đều với bán kính \(R\) và tốc độ góc \(\omega\). Xác định phương trình của dao động điều hòa tương ứng trên trục \(Ox\) và \(Oy\).

   Hướng dẫn:

   • Phương trình chuyển động trên trục \(Ox\): \(x(t) = R\cos(\omega t)\).
   • Phương trình chuyển động trên trục \(Oy\): \(y(t) = R\sin(\omega t)\).
   • Liên hệ giữa chuyển động tròn đều và dao động điều hòa trên mỗi trục để hiểu rõ sự tương đồng.

3. Bài tập 3: Cho một con lắc lò xo dao động với tần số góc \(\omega\) và biên độ \(A\). Tính động năng và thế năng của con lắc tại thời điểm \(t\).

   Hướng dẫn:

   • Động năng: \(W_{đ}(t) = \frac{1}{2}m v^2(t)\), với \(v(t) = -A\omega\sin(\omega t + \varphi)\).
   • Thế năng: \(W_{t}(t) = \frac{1}{2}k x^2(t)\), với \(x(t) = A\cos(\omega t + \varphi)\).
   • Tổng năng lượng: \(W = W_{đ}(t) + W_{t}(t)\), và nhận xét về sự bảo toàn năng lượng trong dao động điều hòa.

Những bài tập trên giúp học sinh không chỉ nắm vững lý thuyết mà còn phát triển khả năng áp dụng vào thực tiễn, từ đó hiểu rõ hơn về mối quan hệ giữa dao động điều hòa và chuyển động tròn đều.

Để nắm vững hơn về mối quan hệ giữa dao động điều hòa và chuyển động tròn đều, dưới đây là một số tài liệu và nguồn học liệu có thể tham khảo:

1. Giáo trình Vật lý lớp 12: Đây là nguồn tài liệu chính thống, cung cấp kiến thức cơ bản về dao động điều hòa và chuyển động tròn đều. Trong chương trình học, các bài giảng và ví dụ đều minh họa rõ ràng sự liên hệ giữa hai dạng chuyển động này.

2. Sách bài tập Vật lý: Các bài tập trong sách bài tập không chỉ giúp củng cố kiến thức mà còn cung cấp các bài toán ứng dụng thực tế liên quan đến dao động điều hòa và chuyển động tròn đều.

3. Bài giảng trực tuyến và video hướng dẫn: Các khóa học trực tuyến, như trên các nền tảng như YouTube hoặc Coursera, cung cấp nhiều bài giảng về lý thuyết và bài tập thực hành. Các video thường minh họa trực quan về sự liên hệ giữa dao động điều hòa và chuyển động tròn đều.

4. Trang web học tập: Một số trang web như VietJack, Hoc24.vn, hoặc VnDoc cung cấp tài liệu học tập và bài tập tự luyện về chủ đề này. Học sinh có thể tham khảo để mở rộng kiến thức và luyện tập.

5. Bài viết và luận văn: Ngoài ra, các bài viết nghiên cứu khoa học, luận văn và tài liệu học thuật từ các trường đại học cũng là nguồn tham khảo quan trọng cho những ai muốn tìm hiểu sâu hơn về lý thuyết và ứng dụng của dao động điều hòa và chuyển động tròn đều.

Những tài liệu trên không chỉ giúp củng cố kiến thức lý thuyết mà còn cung cấp các bài tập và ví dụ thực tế, giúp người học hiểu sâu hơn về sự liên hệ giữa hai dạng chuyển động này.