Đặc Điểm của Chuyển Động Tròn Đều: Khám Phá Chi Tiết và Ứng Dụng Thực Tiễn

Chuyển động tròn đều là một loại chuyển động có quỹ đạo là đường tròn, trong đó vật thể di chuyển với tốc độ không đổi trên mọi cung tròn. Đặc điểm của chuyển động tròn đều được thể hiện qua các yếu tố sau:

1. Vectơ Vận Tốc

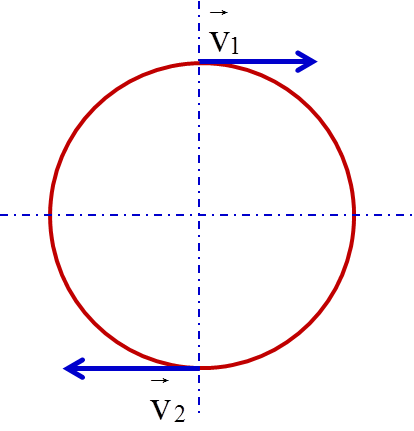
• Độ lớn của vectơ vận tốc không thay đổi.
• Phương của vectơ vận tốc luôn tiếp tuyến với quỹ đạo tròn tại mỗi điểm trên đường tròn.
• Chiều của vectơ vận tốc trùng với chiều chuyển động của vật trên quỹ đạo tròn.

2. Tốc Độ Góc

Tốc độ góc (\(\omega\)) là đại lượng đo bằng góc mà bán kính của quỹ đạo quét được trong một đơn vị thời gian. Tốc độ góc trong chuyển động tròn đều là không đổi và được tính bằng công thức:

\[
\omega = \frac{\Delta \alpha}{\Delta t}
\]

Trong đó:

• \(\Delta \alpha\): Góc quét được (đơn vị radian).
• \(\Delta t\): Thời gian quét (đơn vị giây).

3. Chu Kỳ và Tần Số

Chu kỳ (\(T\)) là thời gian để vật thể đi hết một vòng trên quỹ đạo tròn, được xác định bằng công thức:

\[
T = \frac{2\pi}{\omega}
\]

Tần số (\(f\)) là số vòng mà vật thể đi được trong một giây và có mối liên hệ với chu kỳ như sau:

\[
f = \frac{1}{T}
\]

4. Tốc Độ Dài

Tốc độ dài (\(v\)) là độ lớn tức thời của vận tốc và được liên hệ với tốc độ góc qua công thức:

\[
v = \omega \cdot r
\]

Trong đó:

• \(r\): Bán kính của quỹ đạo tròn.

5. Gia Tốc Hướng Tâm

Trong chuyển động tròn đều, mặc dù tốc độ dài không thay đổi nhưng hướng của vận tốc liên tục thay đổi, dẫn đến sự xuất hiện của gia tốc hướng tâm. Gia tốc hướng tâm (\(a_{ht}\)) luôn hướng vào tâm của quỹ đạo tròn và có độ lớn được tính theo công thức:

\[
a_{ht} = \frac{v^2}{r} = \omega^2 \cdot r
\]

Những đặc điểm này giúp chúng ta hiểu rõ hơn về bản chất và các yếu tố liên quan đến chuyển động tròn đều, từ đó áp dụng vào nhiều bài toán và ứng dụng thực tế.

Chuyển động tròn đều là một dạng chuyển động mà vật thể di chuyển theo quỹ đạo tròn với tốc độ không đổi. Đây là một hiện tượng vật lý phổ biến và có vai trò quan trọng trong nhiều ứng dụng thực tiễn.

• Quỹ đạo: Vật thể trong chuyển động tròn đều có quỹ đạo là một đường tròn. Mọi điểm trên đường tròn đều cách đều tâm, do đó, bán kính quỹ đạo luôn không đổi.
• Tốc độ dài: Trong chuyển động tròn đều, tốc độ dài của vật là không đổi và được tính bằng công thức: \[ v = \frac{\Delta s}{\Delta t} \] Trong đó:
  • \(\Delta s\): Độ dài cung tròn mà vật đi được.
  • \(\Delta t\): Thời gian để đi được cung tròn đó.
• Vận tốc: Vận tốc trong chuyển động tròn đều có độ lớn không thay đổi, nhưng hướng của nó luôn thay đổi theo phương tiếp tuyến với quỹ đạo tại mỗi điểm.
• Tốc độ góc: Tốc độ góc (\(\omega\)) là đại lượng không đổi trong chuyển động tròn đều, được tính bằng góc mà bán kính quét được trong một đơn vị thời gian: \[ \omega = \frac{\Delta \alpha}{\Delta t} \] Trong đó:
  • \(\Delta \alpha\): Góc quét được (đo bằng radian).
  • \(\Delta t\): Thời gian quét (đơn vị giây).
• Gia tốc hướng tâm: Mặc dù tốc độ dài không đổi, nhưng vì hướng vận tốc liên tục thay đổi, vật trong chuyển động tròn đều có gia tốc hướng tâm luôn hướng vào tâm quỹ đạo. Gia tốc hướng tâm (\(a_{ht}\)) được tính bằng công thức: \[ a_{ht} = \frac{v^2}{r} = \omega^2 \cdot r \]

Tổng quan, chuyển động tròn đều không chỉ là một khái niệm quan trọng trong vật lý mà còn có nhiều ứng dụng thực tế, từ chuyển động của các hành tinh đến hoạt động của các thiết bị cơ học như động cơ và bánh xe.

Trong chuyển động tròn đều, có một số đại lượng đặc trưng quan trọng mà chúng ta cần hiểu rõ. Những đại lượng này không chỉ giúp mô tả chuyển động mà còn cho phép tính toán và dự đoán các yếu tố liên quan.

• Tốc độ dài (\(v\)): Tốc độ dài là độ lớn của vận tốc tại mỗi điểm trên quỹ đạo tròn. Được tính bằng công thức: \[ v = \frac{\Delta s}{\Delta t} \] Trong đó:
  • \(\Delta s\): Độ dài cung tròn mà vật đi được.
  • \(\Delta t\): Thời gian để đi hết cung tròn đó.
• Tốc độ góc (\(\omega\)): Tốc độ góc là đại lượng đo bằng góc mà bán kính nối từ tâm quỹ đạo đến vật quét được trong một đơn vị thời gian. Công thức tính: \[ \omega = \frac{\Delta \alpha}{\Delta t} \] Trong đó:
  • \(\Delta \alpha\): Góc quét được (đo bằng radian).
  • \(\Delta t\): Thời gian quét (đơn vị giây).
  Tốc độ góc là không đổi trong chuyển động tròn đều.
• Chu kỳ (\(T\)): Chu kỳ là thời gian để vật đi hết một vòng trên quỹ đạo tròn. Công thức tính chu kỳ: \[ T = \frac{2\pi}{\omega} \] Chu kỳ thường được đo bằng giây (s).
• Tần số (\(f\)): Tần số là số vòng mà vật đi được trong một giây. Tần số và chu kỳ có mối liên hệ với nhau thông qua công thức: \[ f = \frac{1}{T} \] Tần số thường được đo bằng hertz (Hz).
• Gia tốc hướng tâm (\(a_{ht}\)): Gia tốc hướng tâm là gia tốc mà vật phải có để luôn giữ cho nó di chuyển theo quỹ đạo tròn. Gia tốc này luôn hướng vào tâm quỹ đạo và có độ lớn: \[ a_{ht} = \frac{v^2}{r} = \omega^2 \cdot r \] Trong đó:
  • \(r\): Bán kính của quỹ đạo tròn.

Các đại lượng đặc trưng này đóng vai trò quan trọng trong việc hiểu và phân tích chuyển động tròn đều, từ đó áp dụng vào các bài toán thực tiễn và các ứng dụng trong khoa học và kỹ thuật.

Trong chuyển động tròn đều, vận tốc và gia tốc là hai đại lượng quan trọng, đóng vai trò chủ chốt trong việc hiểu rõ bản chất của chuyển động này.

• Vận tốc trong chuyển động tròn đều:

  Vận tốc của một vật trong chuyển động tròn đều có độ lớn không thay đổi, nhưng hướng của nó luôn thay đổi theo thời gian. Vận tốc luôn tiếp tuyến với quỹ đạo tròn tại mỗi điểm, có nghĩa là nó luôn vuông góc với bán kính nối từ tâm đến điểm đó. Độ lớn của vận tốc \(v\) được tính bằng công thức:

  \[
  v = \omega \cdot r
  \]

  Trong đó:

  • \(\omega\): Tốc độ góc.
  • \(r\): Bán kính của quỹ đạo tròn.
• Gia tốc trong chuyển động tròn đều:

  Gia tốc trong chuyển động tròn đều là gia tốc hướng tâm. Mặc dù tốc độ của vật là không đổi, nhưng do hướng của vận tốc liên tục thay đổi, vật vẫn có gia tốc. Gia tốc hướng tâm (\(a_{ht}\)) luôn hướng vào tâm của quỹ đạo và có độ lớn được tính bằng công thức:

  \[
  a_{ht} = \frac{v^2}{r} = \omega^2 \cdot r
  \]

  Trong đó:

  • \(v\): Độ lớn của vận tốc.
  • \(r\): Bán kính của quỹ đạo tròn.

Gia tốc hướng tâm là nguyên nhân khiến vật chuyển động theo quỹ đạo tròn mà không bay ra khỏi quỹ đạo. Nếu không có gia tốc này, vật sẽ tiếp tục di chuyển theo phương tiếp tuyến do quán tính.

Chuyển động tròn đều không chỉ là một hiện tượng lý thuyết mà còn có nhiều ứng dụng quan trọng trong đời sống hàng ngày và khoa học kỹ thuật. Dưới đây là một số ví dụ tiêu biểu và ứng dụng của chuyển động tròn đều.

• Ứng dụng trong công nghệ và kỹ thuật:

  Chuyển động tròn đều là nguyên lý cơ bản trong thiết kế và vận hành của nhiều loại máy móc, chẳng hạn như:

  • Động cơ điện: Các rotor trong động cơ điện quay với tốc độ góc không đổi, tạo ra chuyển động tròn đều để chuyển đổi điện năng thành cơ năng.
  • Máy quay ly tâm: Sử dụng chuyển động tròn đều để tách các chất khác nhau dựa trên khối lượng của chúng.
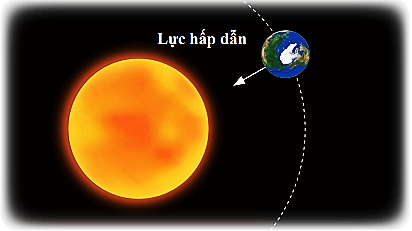
• Ứng dụng trong thiên văn học:

  Các hành tinh trong hệ Mặt Trời quay quanh Mặt Trời theo quỹ đạo gần tròn với tốc độ góc gần như không đổi. Đây là một ví dụ điển hình của chuyển động tròn đều trong tự nhiên.

• Ví dụ thực tế:
  • Chuyển động của bánh xe đạp: Khi xe đạp di chuyển đều, bánh xe quay với tốc độ góc không đổi, tương tự như chuyển động tròn đều.
  • Đồng hồ quả lắc: Chuyển động của kim đồng hồ quanh trục của nó là một ví dụ của chuyển động tròn đều với chu kỳ đều đặn.
• Ứng dụng trong thể thao:

  Trong các môn thể thao như đua xe đạp hoặc đua ô tô, chuyển động tròn đều của bánh xe đóng vai trò quan trọng trong việc duy trì tốc độ và điều hướng.

Nhờ những ứng dụng này, chuyển động tròn đều trở thành một phần không thể thiếu trong nhiều lĩnh vực khác nhau, từ công nghệ, thiên văn học đến các hoạt động hàng ngày.