Chuyển Động Tròn Đều Bán Kính R Có Gia Tốc - Hiểu Rõ Và Ứng Dụng Thực Tiễn

Trong vật lý, chuyển động tròn đều là một dạng chuyển động trong đó vật di chuyển trên một đường tròn với vận tốc không đổi. Tuy nhiên, dù vận tốc tuyến tính không đổi, vật vẫn có gia tốc, gọi là gia tốc hướng tâm, vì hướng của vận tốc luôn thay đổi theo thời gian.

1. Đặc Điểm Của Chuyển Động Tròn Đều

• Chuyển động xảy ra trên một quỹ đạo hình tròn với bán kính \(r\) không đổi.
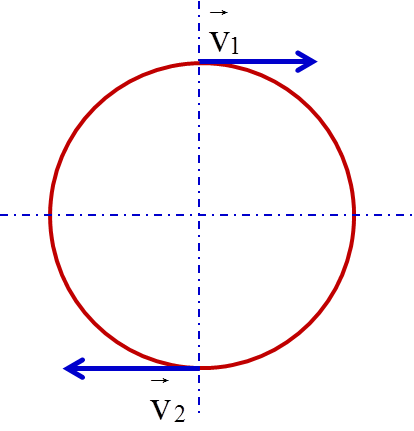
• Vận tốc tuyến tính \(v\) của vật có độ lớn không thay đổi, nhưng phương luôn thay đổi để giữ vật di chuyển trên quỹ đạo tròn.
• Chu kỳ \(T\) là thời gian để vật di chuyển hết một vòng tròn và tần số \(f\) là số vòng vật di chuyển trong một đơn vị thời gian.

2. Gia Tốc Hướng Tâm

Trong chuyển động tròn đều, gia tốc hướng tâm luôn hướng về tâm của quỹ đạo và có độ lớn không đổi. Gia tốc này được tính bằng công thức:

\[
a_h = \frac{v^2}{r}
\]

Trong đó:

• \(a_h\) là gia tốc hướng tâm.
• \(v\) là vận tốc tuyến tính của vật.
• \(r\) là bán kính của quỹ đạo tròn.

3. Ứng Dụng và Ví Dụ

Chuyển động tròn đều và gia tốc hướng tâm có rất nhiều ứng dụng thực tế trong đời sống và kỹ thuật, chẳng hạn như:

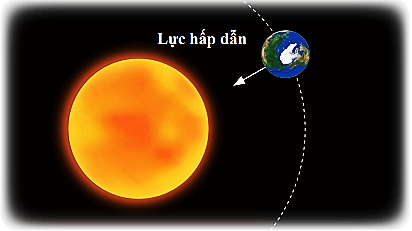
• Một vệ tinh nhân tạo quay quanh Trái Đất với quỹ đạo gần tròn, nơi gia tốc hướng tâm do lực hấp dẫn tạo ra.
• Chuyển động của các bánh xe khi một chiếc xe di chuyển trên đường, với lốp xe quay quanh trục với một vận tốc góc nhất định.
• Một viên đá được buộc vào một sợi dây và quay đều trong không trung, tạo ra lực căng dây do gia tốc hướng tâm.

4. Tóm Lược

Chuyển động tròn đều là một dạng chuyển động quan trọng trong vật lý, đặc trưng bởi vận tốc không đổi và gia tốc hướng tâm. Hiểu rõ về chuyển động này giúp chúng ta giải thích được nhiều hiện tượng trong tự nhiên cũng như ứng dụng trong công nghệ và đời sống hàng ngày.

Chuyển động tròn đều là một dạng chuyển động trong đó một vật di chuyển trên một quỹ đạo hình tròn với vận tốc không đổi về độ lớn. Dù vậy, hướng của vận tốc liên tục thay đổi, do đó vật có gia tốc hướng tâm.

• Quỹ đạo: Vật di chuyển trên một đường tròn với bán kính \(r\) không đổi.
• Vận tốc: Vận tốc tuyến tính \(v\) có độ lớn không thay đổi, được tính bằng công thức: \[ v = \frac{2\pi r}{T} \] trong đó \(T\) là chu kỳ, thời gian để vật đi hết một vòng.
• Gia tốc hướng tâm: Gia tốc này luôn hướng về tâm của quỹ đạo và được xác định bằng công thức: \[ a_h = \frac{v^2}{r} \]

Chuyển động tròn đều được ứng dụng rộng rãi trong thực tiễn, từ chuyển động của vệ tinh quay quanh Trái Đất cho đến các bộ phận máy móc quay đều trong công nghiệp. Hiểu rõ về chuyển động này giúp ta phân tích và giải quyết các bài toán liên quan đến lực và chuyển động trong thực tế.

Trong chuyển động tròn đều, gia tốc là một đại lượng vector đặc trưng cho sự thay đổi của vận tốc theo thời gian. Gia tốc trong chuyển động tròn đều luôn hướng về tâm của quỹ đạo và được gọi là gia tốc hướng tâm.

2.1. Gia Tốc Hướng Tâm

Gia tốc hướng tâm có độ lớn không đổi và phụ thuộc vào vận tốc dài \(v\) và bán kính \(R\) của quỹ đạo chuyển động. Gia tốc hướng tâm được tính theo công thức:

\[
a_{\text{ht}} = \frac{v^2}{R}
\]

Trong đó:

• \(a_{\text{ht}}\): Gia tốc hướng tâm (m/s²)
• \(v\): Vận tốc dài (m/s)
• \(R\): Bán kính quỹ đạo (m)

2.2. Công Thức Tính Gia Tốc

Để tính gia tốc hướng tâm trong một bài toán cụ thể, bạn cần biết hai yếu tố chính là vận tốc dài \(v\) của vật thể và bán kính \(R\) của quỹ đạo. Áp dụng công thức sau:

\[
a_{\text{ht}} = \frac{\omega^2 \cdot R}{v}
\]

Trong đó:

• \(\omega\): Tần số góc (rad/s)
• \(R\): Bán kính quỹ đạo (m)

Nếu biết được vận tốc dài \(v\) và bán kính \(R\), ta cũng có thể suy ra gia tốc hướng tâm qua công thức sau:

\[
a_{\text{ht}} = \omega \cdot v
\]

Việc hiểu rõ về gia tốc trong chuyển động tròn đều là rất quan trọng, đặc biệt là trong các ứng dụng thực tế như thiết kế đường cong trong giao thông hoặc tính toán lực cần thiết để giữ một vật thể trên quỹ đạo tròn.

Chuyển động tròn đều là một hiện tượng vật lý quan trọng với nhiều ứng dụng thực tế trong đời sống và công nghiệp.

• Giao thông: Trong thiết kế đường giao thông, đặc biệt là các đoạn cua của đường ô tô và đường sắt, nguyên lý của chuyển động tròn đều được áp dụng để đảm bảo an toàn cho phương tiện. Độ nghiêng của mặt đường được thiết kế sao cho lực hướng tâm, được tạo ra bởi hợp lực giữa trọng lực và phản lực của mặt đường, giúp xe và tàu không bị trượt ra ngoài khi di chuyển qua các đoạn cua.
• Thiết bị ly tâm: Máy ly tâm sử dụng lực hướng tâm trong chuyển động tròn đều để tách các chất có khối lượng riêng khác nhau. Đây là một ứng dụng phổ biến trong các phòng thí nghiệm và công nghiệp, như tách chất rắn từ chất lỏng trong mẫu máu hay làm giàu uranium trong năng lượng hạt nhân.
• Các thiết bị giải trí: Các tàu lượn siêu tốc trong công viên giải trí sử dụng nguyên lý của chuyển động tròn đều để đảm bảo an toàn cho hành khách khi tàu di chuyển qua các đoạn cua gấp và xoắn ốc.

Những ứng dụng này minh chứng cho vai trò quan trọng của chuyển động tròn đều trong việc thiết kế các hệ thống cơ học, đảm bảo hiệu suất và an toàn trong các ngành công nghiệp khác nhau.

Dưới đây là một số bài tập về chuyển động tròn đều với bán kính \( r \) và có gia tốc hướng tâm. Các bài tập này không chỉ giúp củng cố kiến thức mà còn phát triển khả năng tư duy và giải quyết vấn đề cho học sinh.

• Bài tập 1: Một vật có khối lượng \( m = 2 \, \text{kg} \) chuyển động tròn đều với tốc độ \( v = 4 \, \text{m/s} \) trên quỹ đạo bán kính \( r = 0.5 \, \text{m} \). Tính gia tốc hướng tâm của vật.

Lời giải: Gia tốc hướng tâm được tính theo công thức:

\[ a_{\text{ht}} = \frac{v^2}{r} \]

Thay các giá trị vào công thức:

\[ a_{\text{ht}} = \frac{4^2}{0.5} = 32 \, \text{m/s}^2 \]

Vậy, gia tốc hướng tâm của vật là \( 32 \, \text{m/s}^2 \).

• Bài tập 2: Một vật chuyển động tròn đều với tần số \( f = 2 \, \text{Hz} \) và bán kính quỹ đạo \( r = 1 \, \text{m} \). Tính tốc độ góc \( \omega \) và tốc độ dài \( v \) của vật.

Lời giải: Tốc độ góc \( \omega \) được tính theo công thức:

\[ \omega = 2 \pi f \]

Thay \( f = 2 \, \text{Hz} \) vào công thức:

\[ \omega = 2 \pi \times 2 = 4 \pi \, \text{rad/s} \]

Tốc độ dài \( v \) được tính theo công thức:

\[ v = \omega r = 4 \pi \times 1 = 4 \pi \, \text{m/s} \]

Vậy, tốc độ góc của vật là \( 4 \pi \, \text{rad/s} \) và tốc độ dài là \( 4 \pi \, \text{m/s} \).

• Bài tập 3: Một chiếc xe đi qua một khúc cua với bán kính \( r = 50 \, \text{m} \). Tốc độ của xe là \( 20 \, \text{m/s} \). Tính lực hướng tâm cần thiết để giữ cho xe chuyển động theo quỹ đạo tròn. Giả sử khối lượng của xe là \( 800 \, \text{kg} \).

Lời giải: Lực hướng tâm được tính theo công thức:

\[ F_{\text{ht}} = m \cdot a_{\text{ht}} = m \cdot \frac{v^2}{r} \]

Thay các giá trị vào công thức:

\[ F_{\text{ht}} = 800 \times \frac{20^2}{50} = 6400 \, \text{N} \]

Vậy, lực hướng tâm cần thiết là \( 6400 \, \text{N} \).