Chuyển Động Tròn Đều Nâng Cao: Hướng Dẫn Toàn Diện và Chi Tiết

Chuyển động tròn đều là một dạng chuyển động trong đó một vật di chuyển theo quỹ đạo tròn với tốc độ góc không đổi. Đây là một chủ đề quan trọng trong chương trình Vật lý lớp 10, đặc biệt khi bạn học ở mức độ nâng cao. Bài viết này sẽ cung cấp thông tin chi tiết về lý thuyết và các bài tập liên quan đến chuyển động tròn đều, giúp bạn nắm vững kiến thức và ứng dụng chúng vào giải quyết các bài toán thực tế.

1. Định Nghĩa và Công Thức Cơ Bản

• Độ Dịch Chuyển Góc \(\Delta \theta\): Đây là góc mà một vật di chuyển trên quỹ đạo tròn trong một khoảng thời gian nhất định. Công thức tính: \[ \Delta \theta = \frac{s}{r} \] Trong đó \(s\) là chiều dài cung tròn và \(r\) là bán kính quỹ đạo.
• Tốc Độ Góc \(\omega\): Được xác định bởi sự thay đổi của độ dịch chuyển góc trong một đơn vị thời gian. Công thức: \[ \omega = \frac{\Delta \theta}{\Delta t} \] Đơn vị của tốc độ góc là rad/s.
• Tốc Độ Dài \(v\): Được tính bằng công thức: \[ v = \omega \times r \] Đây là tốc độ của một điểm trên vành ngoài của quỹ đạo tròn.
• Gia Tốc Hướng Tâm \(a\): Được tính bằng: \[ a = \frac{v^2}{r} = \omega^2 \times r \] Đây là gia tốc mà luôn hướng về tâm của quỹ đạo tròn, giữ cho vật di chuyển theo đường tròn.

2. Ứng Dụng và Bài Tập Mẫu

Dưới đây là một số bài tập ứng dụng cơ bản và nâng cao về chuyển động tròn đều:

1. Bài Tập 1: Một lưỡi cưa tròn có đường kính 60 cm quay với chu kỳ 0,2 s. Hãy xác định tốc độ góc và tốc độ dài của một điểm trên vành ngoài của lưỡi cưa.
   Giải: Tốc độ góc \(\omega = 10\) rad/s, tốc độ dài \(v = 9,42\) m/s.
2. Bài Tập 2: Một ô tô có bánh xe bán kính 30 cm, di chuyển đều với tốc độ 64,8 km/h. Tính tốc độ góc, chu kỳ quay của bánh xe và gia tốc hướng tâm của một điểm trên vành ngoài của bánh xe.
3. Bài Tập 3: Trong một máy gia tốc hạt cyclotron, các proton được tăng tốc đạt vận tốc 3000 km/s và di chuyển tròn đều với bán kính 25 cm. Tính thời gian để một proton di chuyển 1/2 vòng và chu kỳ quay của nó.

3. Lý Thuyết Nâng Cao

Khi học ở mức nâng cao, học sinh cần chú ý đến các yếu tố như:

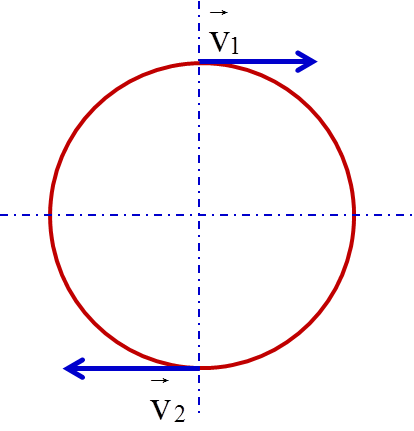
• Sự thay đổi của hướng vận tốc và gia tốc hướng tâm trong quá trình chuyển động.
• Mối liên hệ giữa các đại lượng góc và đại lượng tuyến tính.
• Ứng dụng của chuyển động tròn đều trong các thiết bị thực tế như máy gia tốc hạt, các hệ thống bánh răng, và chuyển động của các hành tinh.

4. Kết Luận

Chuyển động tròn đều là một chủ đề cơ bản nhưng rất quan trọng trong Vật lý, đặc biệt là khi bạn muốn nghiên cứu sâu hơn về động học và động lực học. Việc nắm vững các công thức và biết cách áp dụng chúng vào các bài tập thực tế sẽ giúp bạn tiến xa hơn trong học tập và nghiên cứu.

Chuyển động tròn đều là một loại chuyển động cơ học, trong đó một vật di chuyển theo một quỹ đạo tròn với tốc độ góc không đổi. Đây là một chủ đề cơ bản trong vật lý, đặc biệt quan trọng trong việc nghiên cứu các hệ thống quay như bánh xe, hành tinh, và nhiều ứng dụng khác trong kỹ thuật và đời sống.

Trong chuyển động tròn đều, vật di chuyển với tốc độ tuyến tính không đổi dọc theo một quỹ đạo tròn. Điều này đồng nghĩa với việc vận tốc của vật thay đổi liên tục về hướng nhưng không thay đổi về độ lớn. Một số đặc điểm quan trọng của chuyển động tròn đều bao gồm:

• Quỹ đạo tròn: Vật di chuyển theo một đường tròn cố định có bán kính \(r\).
• Tốc độ góc \(\omega\): Là đại lượng mô tả sự thay đổi của góc mà bán kính quỹ đạo quét được trong một đơn vị thời gian, được tính bằng công thức: \[ \omega = \frac{\Delta \theta}{\Delta t} \] Đơn vị đo tốc độ góc là radian trên giây (rad/s).
• Tốc độ dài \(v\): Là tốc độ của vật di chuyển dọc theo quỹ đạo tròn, được liên hệ với tốc độ góc qua công thức: \[ v = \omega \times r \] Đơn vị đo tốc độ dài là mét trên giây (m/s).
• Gia tốc hướng tâm \(a\): Gia tốc này luôn hướng về tâm của quỹ đạo tròn và được tính bằng công thức: \[ a = \frac{v^2}{r} = \omega^2 \times r \] Gia tốc hướng tâm là yếu tố giữ cho vật di chuyển trên quỹ đạo tròn mà không bị văng ra ngoài.

Chuyển động tròn đều là cơ sở cho nhiều hiện tượng vật lý khác như chuyển động của các hành tinh xung quanh mặt trời, chuyển động của các electron xung quanh hạt nhân, và thậm chí là chuyển động của các bánh xe trong các phương tiện giao thông. Việc hiểu rõ chuyển động tròn đều không chỉ giúp bạn nắm vững kiến thức cơ bản mà còn là nền tảng để nghiên cứu các hiện tượng và ứng dụng phức tạp hơn trong vật lý và kỹ thuật.

Trong chuyển động tròn đều, có một số đại lượng cơ bản cần được hiểu rõ để phân tích và giải các bài toán liên quan. Dưới đây là những đại lượng chính và công thức đi kèm:

• 1. Tốc độ góc \(\omega\):

  Tốc độ góc là đại lượng mô tả mức độ nhanh hay chậm của sự quay quanh trục. Nó được tính bằng công thức:
  \[
  \omega = \frac{\Delta \theta}{\Delta t}
  \]
  Trong đó, \(\Delta \theta\) là góc quay được trong khoảng thời gian \(\Delta t\). Đơn vị của tốc độ góc là radian trên giây (rad/s).

• 2. Chu kỳ \(T\):

  Chu kỳ là thời gian mà vật chuyển động tròn đều cần để hoàn thành một vòng quay. Chu kỳ được liên hệ với tốc độ góc qua công thức:
  \[
  T = \frac{2\pi}{\omega}
  \]
  Đơn vị của chu kỳ là giây (s).

• 3. Tần số \(f\):

  Tần số là số vòng quay mà vật thực hiện được trong một đơn vị thời gian. Nó liên hệ với chu kỳ bằng công thức:
  \[
  f = \frac{1}{T} = \frac{\omega}{2\pi}
  \]
  Đơn vị của tần số là Hertz (Hz).

• 4. Tốc độ dài \(v\):

  Tốc độ dài là tốc độ của một điểm trên quỹ đạo tròn, được tính bằng công thức:
  \[
  v = \omega \times r
  \]
  Trong đó \(r\) là bán kính của quỹ đạo tròn. Đơn vị của tốc độ dài là mét trên giây (m/s).

• 5. Gia tốc hướng tâm \(a_h\):

  Gia tốc hướng tâm là gia tốc mà luôn hướng về tâm của quỹ đạo tròn, giữ cho vật di chuyển theo đường tròn. Nó được tính bằng công thức:
  \[
  a_h = \frac{v^2}{r} = \omega^2 \times r
  \]
  Đơn vị của gia tốc hướng tâm là mét trên giây bình phương (m/s²).

• 6. Lực hướng tâm \(F_h\):

  Lực hướng tâm là lực tác dụng vào vật để giữ cho nó chuyển động theo quỹ đạo tròn, được tính bằng công thức:
  \[
  F_h = m \times a_h = m \times \omega^2 \times r
  \]
  Trong đó \(m\) là khối lượng của vật. Đơn vị của lực hướng tâm là Newton (N).

Hiểu rõ các đại lượng cơ bản trong chuyển động tròn đều không chỉ giúp giải quyết các bài toán lý thuyết mà còn ứng dụng được trong nhiều lĩnh vực thực tiễn như cơ học, kỹ thuật, và thiên văn học.

Chuyển động tròn đều không chỉ dừng lại ở những khái niệm cơ bản mà còn có nhiều khía cạnh phức tạp hơn cần được phân tích kỹ lưỡng. Việc hiểu rõ các lý thuyết nâng cao sẽ giúp chúng ta áp dụng chính xác trong các bài toán phức tạp và các ứng dụng thực tế.

• 1. Mối Quan Hệ Giữa Tốc Độ Góc Và Tốc Độ Dài:

  Tốc độ dài \(v\) và tốc độ góc \(\omega\) của một vật chuyển động tròn đều liên quan trực tiếp với nhau qua bán kính \(r\) của quỹ đạo. Tốc độ dài là đại lượng phụ thuộc vào khoảng cách từ điểm đang xét đến tâm của quỹ đạo tròn:
  \[
  v = \omega \times r
  \]
  Điều này có nghĩa là, với cùng một tốc độ góc, các điểm xa tâm sẽ có tốc độ dài lớn hơn.

• 2. Ảnh Hưởng Của Lực Hướng Tâm Đến Chuyển Động:

  Lực hướng tâm \(F_h\) là lực giữ cho vật di chuyển trên quỹ đạo tròn mà không bị văng ra ngoài. Theo định luật II Newton, lực này tỷ lệ thuận với khối lượng \(m\) của vật và gia tốc hướng tâm \(a_h\):
  \[
  F_h = m \times \omega^2 \times r
  \]
  Khi tốc độ góc tăng hoặc bán kính quỹ đạo giảm, lực hướng tâm cần thiết sẽ tăng lên đáng kể. Điều này giải thích tại sao các vật thể như vệ tinh cần một lực rất lớn để duy trì quỹ đạo quanh Trái Đất.

• 3. Năng Lượng Trong Chuyển Động Tròn Đều:

  Năng lượng cơ học trong chuyển động tròn đều bao gồm động năng do tốc độ dài của vật. Động năng này được tính bằng công thức:
  \[
  K = \frac{1}{2} m v^2 = \frac{1}{2} m (\omega \times r)^2
  \]
  Năng lượng này không đổi trong chuyển động tròn đều, vì tốc độ dài \(v\) và khối lượng \(m\) không thay đổi.

• 4. Ứng Dụng Trong Thiết Kế Máy Móc và Kỹ Thuật:

  Chuyển động tròn đều có nhiều ứng dụng quan trọng trong kỹ thuật, đặc biệt là trong thiết kế các bộ phận quay như bánh răng, trục quay, và các thiết bị cơ khí khác. Việc tính toán chính xác các đại lượng như lực hướng tâm và tốc độ góc giúp đảm bảo sự ổn định và an toàn cho các thiết bị khi vận hành ở tốc độ cao.

Phân tích lý thuyết nâng cao về chuyển động tròn đều không chỉ giúp chúng ta hiểu rõ hơn về các nguyên lý cơ bản, mà còn mở ra cánh cửa ứng dụng trong các lĩnh vực như cơ khí, hàng không, và khoa học không gian.

Dưới đây là một số bài tập giúp củng cố và nâng cao kiến thức về chuyển động tròn đều. Các bài tập này bao gồm nhiều dạng khác nhau, từ cơ bản đến nâng cao, giúp bạn rèn luyện khả năng phân tích và giải quyết vấn đề.

• Bài Tập 1:

  Một vật có khối lượng \(m = 2\) kg chuyển động tròn đều với bán kính quỹ đạo \(r = 0.5\) m và tốc độ góc \(\omega = 4\) rad/s. Tính tốc độ dài và lực hướng tâm của vật.

  Gợi ý: Sử dụng công thức:
  \[
  v = \omega \times r
  \]
  \[
  F_h = m \times \omega^2 \times r
  \]

• Bài Tập 2:

  Một vệ tinh nhân tạo quay quanh Trái Đất theo quỹ đạo tròn với bán kính quỹ đạo \(r = 7000\) km. Tính tốc độ góc của vệ tinh khi chu kỳ quay của nó là 90 phút.

  Gợi ý: Chu kỳ \(T\) và tốc độ góc \(\omega\) liên hệ với nhau qua công thức:
  \[
  \omega = \frac{2\pi}{T}
  \]

• Bài Tập 3:

  Một điểm nằm trên mép của bánh xe có bán kính \(r = 0.3\) m đang quay đều với tốc độ \(120\) vòng/phút. Tính tốc độ dài của điểm này.

  Gợi ý: Trước tiên, chuyển đổi tốc độ quay về đơn vị rad/s, sau đó sử dụng công thức:
  \[
  v = \omega \times r
  \]

• Bài Tập 4:

  Một vật chuyển động tròn đều trên quỹ đạo có bán kính \(r\) với tốc độ dài \(v\). Nếu lực hướng tâm tác dụng lên vật là \(F_h = 50\) N và khối lượng của vật là \(m = 5\) kg, hãy tìm gia tốc hướng tâm và tốc độ góc của vật.

  Gợi ý: Sử dụng công thức:
  \[
  a_h = \frac{F_h}{m}
  \]
  \[
  \omega = \frac{v}{r}
  \]

Những bài tập trên không chỉ giúp bạn ôn lại các khái niệm cơ bản mà còn nâng cao khả năng áp dụng các công thức vào các tình huống thực tế, từ đó hiểu rõ hơn về chuyển động tròn đều.

Chuyển động tròn đều không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng trong thực tế. Hiểu rõ các bài toán thực tế liên quan đến chuyển động tròn đều sẽ giúp chúng ta áp dụng kiến thức một cách chính xác và hiệu quả.

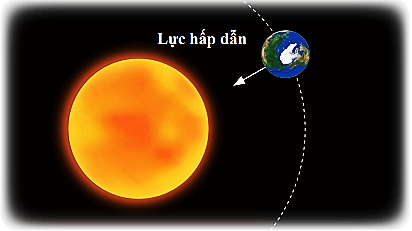
• 1. Chuyển Động Của Các Hành Tinh Quanh Mặt Trời:

  Các hành tinh trong hệ Mặt Trời chuyển động quanh Mặt Trời theo các quỹ đạo gần như tròn đều. Từ đó, chúng ta có thể tính toán các đại lượng như tốc độ dài, tốc độ góc, và chu kỳ của hành tinh bằng cách áp dụng các công thức của chuyển động tròn đều. Ví dụ, tốc độ dài của Trái Đất quanh Mặt Trời có thể tính bằng:
  \[
  v = \omega \times r
  \]

• 2. Chuyển Động Của Vệ Tinh Nhân Tạo:

  Các vệ tinh nhân tạo quay quanh Trái Đất cũng chuyển động tròn đều. Bằng cách sử dụng các công thức liên quan, ta có thể xác định lực hướng tâm cần thiết để giữ vệ tinh trên quỹ đạo cũng như tính toán chu kỳ quay của vệ tinh. Công thức lực hướng tâm:
  \[
  F_h = m \times \omega^2 \times r
  \]
  được sử dụng để đảm bảo vệ tinh không bị rơi xuống Trái Đất hoặc bay ra ngoài không gian.

• 3. Ứng Dụng Trong Thiết Kế Máy Móc:

  Chuyển động tròn đều được áp dụng rộng rãi trong thiết kế các bộ phận quay của máy móc, như bánh răng, trục quay, và bánh xe. Việc hiểu rõ chuyển động này giúp các kỹ sư tính toán được tốc độ quay, lực tác động, và các yếu tố liên quan khác để đảm bảo an toàn và hiệu suất của máy móc. Tốc độ quay của các bộ phận này được tính bằng cách sử dụng công thức tốc độ góc:
  \[
  \omega = \frac{2\pi}{T}
  \]

• 4. Tính Toán Trong Các Trò Chơi Giải Trí:

  Trong các trò chơi giải trí như vòng đu quay hay các thiết bị quay khác, chuyển động tròn đều được ứng dụng để thiết kế tốc độ quay sao cho an toàn và thú vị cho người chơi. Các tính toán về gia tốc hướng tâm, lực hướng tâm giúp đảm bảo rằng người chơi không cảm thấy quá mạnh hoặc quá yếu khi tham gia trò chơi.

Những bài toán thực tế liên quan đến chuyển động tròn đều là minh chứng cho sự quan trọng của lý thuyết này trong cuộc sống hàng ngày. Việc áp dụng chính xác các công thức và nguyên lý giúp chúng ta hiểu rõ hơn và có thể thiết kế, kiểm soát nhiều hệ thống hoạt động một cách hiệu quả.

Qua các phần đã trình bày, chúng ta có thể thấy rằng chuyển động tròn đều là một khái niệm cơ bản nhưng có nhiều ứng dụng quan trọng trong cả lý thuyết và thực tế. Từ việc hiểu các đại lượng cơ bản như tốc độ góc, tốc độ dài, lực hướng tâm, cho đến việc áp dụng vào các bài toán thực tế, mỗi khía cạnh đều đóng vai trò quan trọng trong việc xây dựng nền tảng vững chắc cho các ứng dụng kỹ thuật và khoa học.

Những bài tập và ví dụ thực tế đã giúp chúng ta củng cố kiến thức, đồng thời phát triển khả năng phân tích và giải quyết vấn đề. Chuyển động tròn đều không chỉ đơn thuần là một nội dung lý thuyết, mà còn mở ra nhiều cơ hội để áp dụng trong các lĩnh vực như kỹ thuật cơ khí, thiên văn học, và đời sống hàng ngày.

Nhìn chung, việc nắm vững và áp dụng các khái niệm nâng cao về chuyển động tròn đều sẽ giúp chúng ta không chỉ hiểu rõ hơn về các hiện tượng vật lý, mà còn góp phần vào việc cải tiến, phát triển các hệ thống và công nghệ hiện đại. Đây là một trong những bước tiến quan trọng trong hành trình chinh phục tri thức và khoa học.