Chuyển Động Tròn Đều Đều Có: Khái Niệm, Công Thức và Ứng Dụng

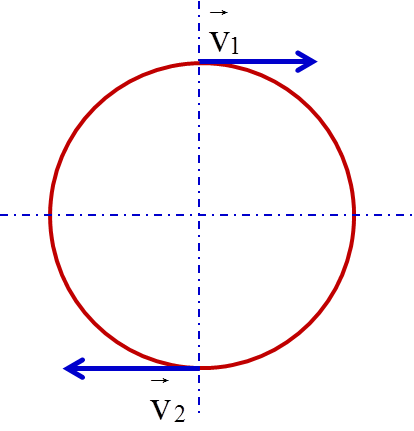
Chuyển động tròn đều là một dạng chuyển động trong đó vật di chuyển theo quỹ đạo hình tròn với tốc độ góc không đổi. Trong chuyển động tròn đều, các đại lượng như tốc độ dài, gia tốc hướng tâm và chu kỳ có những mối quan hệ chặt chẽ với nhau.

Các Đại Lượng Cơ Bản

• Chu kỳ \((T)\): Thời gian để vật thực hiện một vòng trên quỹ đạo tròn. Đơn vị: giây (s).
• Tần số \((f)\): Số vòng quay mà vật thực hiện trong một giây. Công thức: \(f = \frac{1}{T}\), đơn vị là Hz.
• Vận tốc góc \((\omega)\): Đại lượng đo bằng góc mà bán kính quỹ đạo quét được trong một đơn vị thời gian. Công thức: \(\omega = \frac{2\pi}{T}\), đơn vị: rad/s.
• Vận tốc dài \((v)\): Độ lớn của vận tốc của vật di chuyển theo quỹ đạo tròn. Công thức: \(v = r\omega\), trong đó \(r\) là bán kính của quỹ đạo.
• Gia tốc hướng tâm \((a_{ht})\): Gia tốc luôn hướng vào tâm của quỹ đạo, duy trì vật di chuyển theo quỹ đạo tròn. Công thức: \(a_{ht} = \frac{v^2}{r} = r\omega^2\).

Các Mối Quan Hệ Giữa Các Đại Lượng

Trong chuyển động tròn đều, các đại lượng trên có các mối quan hệ sau:

• Công thức liên hệ giữa chu kỳ và vận tốc góc:

\[
T = \frac{2\pi}{\omega}
\]

• Công thức liên hệ giữa tần số và chu kỳ:

\[
f = \frac{1}{T}
\]

• Công thức liên hệ giữa vận tốc dài và vận tốc góc:

\[
v = r\omega
\]

• Công thức tính gia tốc hướng tâm:

\[
a_{ht} = \frac{v^2}{r} = r\omega^2
\]

Ứng Dụng Của Chuyển Động Tròn Đều

Chuyển động tròn đều được ứng dụng rộng rãi trong nhiều lĩnh vực như kỹ thuật, thiên văn học, và trong đời sống hàng ngày. Ví dụ, sự quay của các hành tinh quanh mặt trời là một dạng chuyển động tròn đều, hay trong kỹ thuật, chuyển động quay của bánh xe máy móc cũng là một ví dụ điển hình.

Bài Tập Minh Họa

1. Tính chu kỳ của một vật thực hiện chuyển động tròn đều với tần số \(f = 5\) Hz.
2. Tính gia tốc hướng tâm của một vật chuyển động tròn đều với bán kính quỹ đạo \(r = 2\) m và vận tốc dài \(v = 10\) m/s.
3. Xác định vận tốc góc của một vật chuyển động tròn đều có chu kỳ \(T = 2\) giây.

Kết Luận

Chuyển động tròn đều là một hiện tượng cơ bản trong vật lý, giúp chúng ta hiểu rõ hơn về các quy luật chuyển động và các đại lượng liên quan. Nắm vững các khái niệm và công thức liên quan sẽ giúp ích rất nhiều trong việc giải quyết các bài toán vật lý phức tạp hơn.

Chuyển động tròn đều là một dạng chuyển động cơ bản trong vật lý học, trong đó vật thể di chuyển theo quỹ đạo tròn với tốc độ không đổi. Đây là trường hợp đặc biệt của chuyển động tròn, nơi mà mô đun của vận tốc là không đổi và hướng của vận tốc thay đổi liên tục theo thời gian.

Trong chuyển động tròn đều, có các đại lượng quan trọng sau:

• Chu kỳ (T): Là thời gian để vật di chuyển hết một vòng quỹ đạo. Chu kỳ được tính bằng công thức \[ T = \frac{1}{f} \], trong đó \( f \) là tần số của chuyển động.
• Tần số (f): Là số vòng quay mà vật thực hiện trong một đơn vị thời gian. Tần số có đơn vị là Hertz (Hz).
• Vận tốc góc (ω): Là tốc độ thay đổi góc của vật, được tính bằng công thức \[ \omega = \frac{2\pi}{T} \]. Vận tốc góc có đơn vị là radian trên giây (rad/s).
• Vận tốc dài (v): Là tốc độ di chuyển của vật trên quỹ đạo tròn, được liên hệ với vận tốc góc bởi công thức \[ v = \omega r \], trong đó \( r \) là bán kính của quỹ đạo.
• Gia tốc hướng tâm (a_ht): Là gia tốc luôn hướng vào tâm của quỹ đạo, giữ cho vật di chuyển theo đường tròn. Gia tốc hướng tâm được tính bằng công thức \[ a_{ht} = \frac{v^2}{r} = \omega^2 r \].

Chuyển động tròn đều có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật, từ việc phân tích quỹ đạo của các thiên thể đến thiết kế các thiết bị cơ học như bánh xe, máy quay ly tâm, và các hệ thống vận chuyển.

Chuyển động tròn đều là một dạng chuyển động trong đó một vật thể di chuyển theo quỹ đạo tròn với tốc độ không đổi. Dưới đây là các công thức quan trọng liên quan đến chuyển động tròn đều:

• Chu kỳ (T): Chu kỳ là thời gian để vật thể hoàn thành một vòng tròn. Công thức tính chu kỳ là: \[ T = \frac{2\pi r}{v} \] trong đó:
  • \( T \) là chu kỳ (đơn vị: giây).
  • \( r \) là bán kính quỹ đạo (đơn vị: mét).
  • \( v \) là vận tốc dài của vật (đơn vị: mét/giây).
• Tần số (f): Tần số là số vòng mà vật thể hoàn thành trong một đơn vị thời gian. Công thức tính tần số là: \[ f = \frac{1}{T} \] trong đó \( T \) là chu kỳ.
• Vận tốc góc (ω): Vận tốc góc là tốc độ thay đổi góc của vật thể trong chuyển động tròn đều, được tính bằng công thức: \[ \omega = \frac{2\pi}{T} = \frac{v}{r} \] trong đó:
  • \( \omega \) là vận tốc góc (đơn vị: rad/s).
  • \( v \) là vận tốc dài của vật.
  • \( r \) là bán kính quỹ đạo.
• Gia tốc hướng tâm (a_ht): Gia tốc hướng tâm là gia tốc của vật thể luôn hướng về tâm của quỹ đạo tròn, giữ cho vật thể di chuyển theo quỹ đạo này. Công thức tính gia tốc hướng tâm là: \[ a_{ht} = \frac{v^2}{r} = \omega^2 r \] trong đó:
  • \( a_{ht} \) là gia tốc hướng tâm (đơn vị: m/s²).
  • \( v \) là vận tốc dài.
  • \( r \) là bán kính quỹ đạo.
• Vận tốc dài (v): Vận tốc dài của vật thể di chuyển theo quỹ đạo tròn đều được tính bằng công thức: \[ v = \omega r \] trong đó:
  • \( v \) là vận tốc dài (đơn vị: m/s).
  • \( \omega \) là vận tốc góc.
  • \( r \) là bán kính quỹ đạo.

Các công thức này là nền tảng cho việc phân tích và tính toán trong các bài toán liên quan đến chuyển động tròn đều, và có thể áp dụng trong nhiều lĩnh vực như cơ học, thiên văn học và kỹ thuật.

Dưới đây là một số bài tập cơ bản và nâng cao về chuyển động tròn đều, giúp bạn củng cố kiến thức và áp dụng các công thức đã học vào thực tiễn.

Bài Tập 1: Tính Chu Kỳ và Tần Số

Cho một bánh xe quay đều với vận tốc góc \(\omega = 2\pi \, \text{rad/s}\). Tính chu kỳ và tần số của chuyển động.

• Lời giải:


Chu kỳ \(T\) được tính bằng công thức:
\[
T = \frac{2\pi}{\omega} = \frac{2\pi}{2\pi} = 1 \, \text{s}
\]
Tần số \(f\) được tính bằng công thức:
\[
f = \frac{1}{T} = \frac{1}{1} = 1 \, \text{Hz}
\]

Bài Tập 2: Tính Vận Tốc Góc

Một đĩa tròn có bán kính \(R = 0,3 \, \text{m}\) quay đều với tần số \(f = 5 \, \text{Hz}\). Tính vận tốc góc của đĩa.

• Lời giải:


Vận tốc góc \(\omega\) được tính bằng công thức:
\[
\omega = 2\pi f = 2\pi \times 5 = 10\pi \, \text{rad/s}
\]

Bài Tập 3: Tính Gia Tốc Hướng Tâm

Một vệ tinh quay quanh Trái Đất ở độ cao 400km với thời gian hoàn thành một vòng quay là 90 phút. Tính gia tốc hướng tâm của vệ tinh. Biết bán kính Trái Đất là 6389km.

• Lời giải:


Bán kính quỹ đạo \(r = 6389 \, \text{km} + 400 \, \text{km} = 6789 \, \text{km}\).

Thời gian \(T = 90 \, \text{phút} = 5400 \, \text{s}\).

Tần số góc \(\omega\) được tính bằng:
\[
\omega = \frac{2\pi}{T} = \frac{2\pi}{5400} \, \text{rad/s}
\]
Gia tốc hướng tâm \(a_{ht}\) được tính bằng:
\[
a_{ht} = \omega^2 \times r = \left(\frac{2\pi}{5400}\right)^2 \times 6789 \times 10^3 \, \text{m/s}^2
\]

Bài Tập 4: Vận Tốc Dài

Một điểm trên vành ngoài của bánh xe có bán kính \(0,5 \, \text{m}\) quay với vận tốc góc \(10 \, \text{rad/s}\). Tính vận tốc dài của điểm đó.

• Lời giải:


Vận tốc dài \(v\) được tính bằng công thức:
\[
v = \omega \times r = 10 \, \text{rad/s} \times 0,5 \, \text{m} = 5 \, \text{m/s}
\]