Chuyển Động Tròn Đều Vật Lý 10: Hướng Dẫn Chi Tiết và Bài Tập Thực Hành

Chuyển động tròn đều là một phần quan trọng trong chương trình Vật Lý lớp 10, nơi học sinh được học về các khái niệm liên quan đến quỹ đạo tròn, vận tốc góc, tốc độ dài, và gia tốc hướng tâm. Dưới đây là tổng hợp các nội dung chính về chuyển động tròn đều:

1. Định nghĩa Chuyển Động Tròn Đều

Chuyển động tròn đều là chuyển động của một vật theo một quỹ đạo tròn với tốc độ không đổi. Tốc độ này có thể được biểu diễn qua tốc độ dài và tốc độ góc.

2. Công thức Liên Quan

• Tốc độ dài: \( v = r \cdot \omega \)
• Tốc độ góc: \( \omega = \dfrac{\Delta \alpha}{\Delta t} \)
• Chu kỳ (T): \( T = \dfrac{2\pi}{\omega} \)
• Tần số (f): \( f = \dfrac{1}{T} \)
• Gia tốc hướng tâm: \( a_{ht} = \dfrac{v^2}{r} = r \cdot \omega^2 \)

3. Đặc điểm Vận Tốc và Gia Tốc

Trong chuyển động tròn đều:

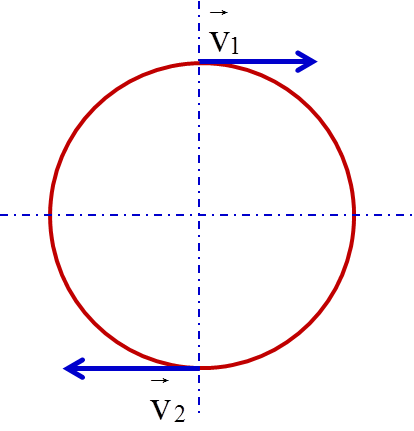
• Véc tơ vận tốc có phương tiếp tuyến với quỹ đạo tròn tại mỗi điểm.
• Gia tốc hướng tâm luôn hướng về tâm của quỹ đạo, giữ cho vật di chuyển theo quỹ đạo tròn.

4. Ứng Dụng trong Thực Tiễn

Chuyển động tròn đều có nhiều ứng dụng trong đời sống hàng ngày và trong các thiết bị công nghiệp như:

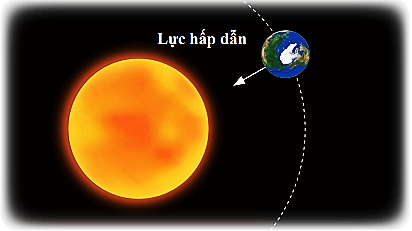
• Chuyển động của các hành tinh xung quanh Mặt Trời.
• Chuyển động của cánh quạt trong các thiết bị làm mát.
• Vòng quay của các bánh xe trong các phương tiện giao thông.

5. Bài Tập Vận Dụng

Dưới đây là một số bài tập thường gặp về chuyển động tròn đều trong chương trình Vật Lý 10:

1. Tính tốc độ góc của một vật chuyển động tròn đều với chu kỳ \( T = 5 \) giây.
2. Một đĩa quay với tốc độ dài \( v = 2 \) m/s và bán kính \( r = 0,5 \) m. Tính tốc độ góc và gia tốc hướng tâm của đĩa.
3. Chứng minh công thức liên hệ giữa tốc độ dài và tốc độ góc.

6. Kết Luận

Hiểu rõ về chuyển động tròn đều không chỉ giúp nắm vững kiến thức Vật Lý cơ bản mà còn giúp áp dụng vào các hiện tượng tự nhiên và các ứng dụng kỹ thuật trong cuộc sống. Việc rèn luyện qua các bài tập giúp học sinh củng cố và ứng dụng lý thuyết vào thực tế.

Chuyển động tròn đều là chuyển động có quỹ đạo là một đường tròn và tốc độ góc không đổi. Dưới đây là các công thức quan trọng trong chuyển động tròn đều:

2.1 Tốc Độ Dài

Tốc độ dài (v) của một vật trong chuyển động tròn đều được tính bằng công thức:

\[
v = \frac{2\pi R}{T} = R\omega
\]

• v: Tốc độ dài (m/s)
• R: Bán kính quỹ đạo (m)
• T: Chu kỳ (s)
• \(\omega\): Tốc độ góc (rad/s)

2.2 Tốc Độ Góc

Tốc độ góc (\(\omega\)) trong chuyển động tròn đều được xác định bởi:

\[
\omega = \frac{\Delta \theta}{\Delta t} = \frac{2\pi}{T}
\]

• \(\omega\): Tốc độ góc (rad/s)
• \(\Delta \theta\): Góc quét được trong khoảng thời gian \(\Delta t\)
• T: Chu kỳ (s)

2.3 Chu Kỳ và Tần Số

Chu kỳ (T) và tần số (f) có mối quan hệ nghịch đảo với nhau, được tính bởi các công thức:

\[
T = \frac{2\pi}{\omega} = \frac{1}{f}
\]

\[
f = \frac{1}{T} = \frac{\omega}{2\pi}
\]

• T: Chu kỳ (s)
• f: Tần số (Hz)

2.4 Gia Tốc Hướng Tâm

Gia tốc hướng tâm (a_ht) là gia tốc gây ra sự thay đổi hướng của vận tốc, và được tính bằng:

\[
a_{ht} = \frac{v^2}{R} = R\omega^2
\]

• a_ht: Gia tốc hướng tâm (m/s²)
• v: Tốc độ dài (m/s)
• R: Bán kính quỹ đạo (m)
• \(\omega\): Tốc độ góc (rad/s)

Trong chuyển động tròn đều, vận tốc và gia tốc là hai đại lượng có vai trò quan trọng trong việc xác định các đặc tính của chuyển động. Dưới đây là chi tiết về đặc điểm của vận tốc và gia tốc trong chuyển động tròn đều.

3.1 Vận Tốc Trong Chuyển Động Tròn Đều

Vận tốc trong chuyển động tròn đều có những đặc điểm sau:

• Độ lớn: Vận tốc có độ lớn không thay đổi và được tính bằng công thức:

\[ v = \omega \cdot r \]

• Hướng: Mặc dù độ lớn của vận tốc không đổi, nhưng hướng của vận tốc luôn thay đổi. Vận tốc luôn tiếp tuyến với quỹ đạo tại mỗi điểm, và luôn vuông góc với bán kính của đường tròn.

3.2 Gia Tốc Hướng Tâm

Gia tốc trong chuyển động tròn đều được gọi là gia tốc hướng tâm, với những đặc điểm như sau:

• Hướng: Gia tốc hướng tâm luôn hướng về tâm của quỹ đạo, đảm bảo rằng vật luôn chuyển động theo đường tròn.
• Độ lớn: Độ lớn của gia tốc hướng tâm được tính bằng công thức:

\[ a_{ht} = \frac{v^2}{r} = \omega^2 \cdot r \]

• Đơn vị của gia tốc hướng tâm là \( m/s^2 \).

3.3 Kết Luận

Như vậy, trong chuyển động tròn đều, vận tốc có độ lớn không đổi nhưng hướng luôn thay đổi. Gia tốc hướng tâm là gia tốc duy nhất trong chuyển động này và nó có hướng luôn luôn hướng về tâm của quỹ đạo. Nhờ đặc điểm này, chuyển động tròn đều là một dạng chuyển động phức tạp nhưng cũng rất quy luật và dễ dự đoán.

Dưới đây là một số bài tập giúp các bạn ôn luyện và hiểu rõ hơn về chuyển động tròn đều, kèm theo các bước giải chi tiết:

4.1 Bài Tập Tính Toán Tốc Độ

1. Bài toán: Một lưỡi cưa tròn có đường kính 60 cm quay đều với chu kỳ 0,2 s. Hãy tính tốc độ góc và tốc độ dài của một điểm trên vành ngoài của lưỡi cưa.

   Giải:

   • Chu kỳ quay: \(T = 0,2\) s
   • Bán kính: \(r = 30\) cm = 0,3 m
   • Tốc độ góc: \(\omega = \frac{2\pi}{T} = \frac{2\pi}{0,2} = 10\) rad/s
   • Tốc độ dài: \(v = \omega \times r = 10 \times 0,3 = 3\) m/s

2. Bài toán: Một chất điểm chuyển động đều trên một quỹ đạo tròn có bán kính 40 cm. Biết rằng trong một phút nó đi được 300 vòng. Hãy xác định tốc độ góc, tốc độ dài và gia tốc hướng tâm của chất điểm.

   Giải:

   • Bán kính: \(r = 40\) cm = 0,4 m
   • Số vòng quay: 300 vòng/phút = 5 vòng/giây
   • Tốc độ góc: \(\omega = 2\pi \times 5 = 10\pi\) rad/s
   • Tốc độ dài: \(v = \omega \times r = 10\pi \times 0,4 = 4\pi\) m/s
   • Gia tốc hướng tâm: \(a_{ht} = \omega^2 \times r = (10\pi)^2 \times 0,4 = 400\pi^2\) m/s²

4.2 Bài Tập Tính Gia Tốc

1. Bài toán: Một ô tô có bánh xe bán kính 30 cm, chuyển động đều với tốc độ 64,8 km/h. Hãy tính tốc độ góc, chu kỳ quay của bánh xe và gia tốc hướng tâm của một điểm trên vành ngoài của bánh xe.

   Giải:

   • Bán kính: \(r = 30\) cm = 0,3 m
   • Tốc độ dài: \(v = 64,8\) km/h = 18 m/s
   • Tốc độ góc: \(\omega = \frac{v}{r} = \frac{18}{0,3} = 60\) rad/s
   • Chu kỳ quay: \(T = \frac{2\pi}{\omega} = \frac{2\pi}{60} \approx 0,1047\) s
   • Gia tốc hướng tâm: \(a_{ht} = \omega^2 \times r = 60^2 \times 0,3 = 1080\) m/s²

4.3 Bài Tập Tính Chu Kỳ và Tần Số

1. Bài toán: Một bánh xe có bán kính 0,5 m quay đều với tốc độ 20 vòng/phút. Hãy tính chu kỳ, tần số, tốc độ góc và tốc độ dài của một điểm trên vành bánh xe.

   Giải:

   • Tần số quay: \(f = 20\) vòng/phút = \(\frac{20}{60}\) Hz = \(\frac{1}{3}\) Hz
   • Chu kỳ: \(T = \frac{1}{f} = 3\) s
   • Tốc độ góc: \(\omega = 2\pi \times f = 2\pi \times \frac{1}{3} \approx 2,09\) rad/s
   • Tốc độ dài: \(v = \omega \times r = 2,09 \times 0,5 \approx 1,045\) m/s

Chuyển động tròn đều là một hiện tượng vật lý quan trọng với nhiều ứng dụng thực tiễn trong đời sống và khoa học. Dưới đây là một số ứng dụng điển hình:

5.1 Trong Thiên Văn Học

Chuyển động tròn đều được áp dụng trong việc nghiên cứu quỹ đạo của các hành tinh, mặt trăng và các vật thể thiên văn. Ví dụ:

• Quỹ đạo của các hành tinh quanh Mặt Trời có thể coi là chuyển động tròn đều với tốc độ góc không đổi.
• Hệ thống vệ tinh quay quanh Trái Đất cũng được phân tích dựa trên nguyên lý chuyển động tròn đều, giúp duy trì quỹ đạo ổn định.

5.2 Trong Kỹ Thuật và Đời Sống

Chuyển động tròn đều được áp dụng trong nhiều thiết bị kỹ thuật và hoạt động hàng ngày:

• Đồng hồ cơ: Bánh răng trong đồng hồ cơ quay đều theo nguyên lý chuyển động tròn đều, đảm bảo đồng hồ hoạt động chính xác.
• Động cơ điện: Rôto của động cơ điện quay với tốc độ đều, giúp máy móc hoạt động liên tục và hiệu quả.
• Vòng quay trò chơi: Các thiết bị như vòng quay trong khu vui chơi cũng áp dụng nguyên lý này để tạo ra sự ổn định và an toàn cho người sử dụng.
• Máy giặt: Lồng giặt chuyển động tròn đều khi vắt quần áo, tạo ra lực ly tâm giúp quá trình giặt hiệu quả hơn.

5.3 Tính Toán Trong Kỹ Thuật

Các công thức liên quan đến chuyển động tròn đều được sử dụng để tính toán:

• Gia tốc hướng tâm \[ a = \frac{v^2}{r} \]
• Tần số quay \[ f = \frac{1}{T} \]
• Vận tốc góc \[ \omega = \frac{2\pi}{T} \]

Những ứng dụng trên cho thấy tầm quan trọng của chuyển động tròn đều trong cả nghiên cứu khoa học lẫn đời sống hàng ngày, từ các thiết bị hàng ngày đến các hệ thống thiên văn phức tạp.

Chuyển động tròn đều là một chủ đề quan trọng trong chương trình Vật lý 10, cung cấp nền tảng vững chắc cho các khái niệm phức tạp hơn. Để hiểu rõ về chuyển động này, bạn cần nắm vững các công thức về tốc độ góc, gia tốc hướng tâm, và mối quan hệ giữa chu kỳ và tần số. Đồng thời, việc làm quen với các bài tập liên quan sẽ giúp bạn áp dụng lý thuyết vào thực tế.

• Hãy chú ý các công thức quan trọng như: \[ T = \frac{2\pi}{\omega} \] và \[ a_{ht} = \frac{v^2}{r} = r\omega^2 \].
• Ôn tập đều đặn và luyện tập với các bài tập từ cơ bản đến nâng cao là cách tốt nhất để củng cố kiến thức.
• Sử dụng tài liệu tham khảo và các bài giảng trực tuyến để mở rộng hiểu biết của bạn về chủ đề này.

Cuối cùng, kiên nhẫn và thực hành sẽ giúp bạn đạt kết quả tốt trong học tập môn Vật lý. Đừng quên giải quyết các câu hỏi trắc nghiệm và bài tập SGK để chuẩn bị tốt cho các kỳ thi sắp tới.