Chủ đề lý 10 chuyển động thẳng biến đổi đều: Chuyển động thẳng biến đổi đều là một trong những chủ đề quan trọng trong chương trình Vật lý lớp 10. Bài viết này cung cấp kiến thức cơ bản và các bài tập minh họa giúp học sinh nắm vững các khái niệm liên quan. Tham khảo ngay để củng cố hiểu biết và chuẩn bị tốt hơn cho các bài kiểm tra!
Mục lục
- Chuyển Động Thẳng Biến Đổi Đều - Vật Lý 10
- 1. Khái niệm về chuyển động thẳng biến đổi đều
- 2. Công thức tính gia tốc và quãng đường trong chuyển động thẳng biến đổi đều
- 3. Đồ thị chuyển động thẳng biến đổi đều
- 4. Bài tập minh họa về chuyển động thẳng biến đổi đều
- 5. Luyện tập: Bài tập tự luận và trắc nghiệm
Chuyển Động Thẳng Biến Đổi Đều - Vật Lý 10
Trong chương trình Vật lý lớp 10, chuyển động thẳng biến đổi đều là một phần quan trọng giúp học sinh hiểu rõ về các nguyên lý cơ bản của chuyển động trong cơ học. Chủ đề này bao gồm các khái niệm như vận tốc, gia tốc và các công thức tính toán liên quan đến chuyển động.
1. Định Nghĩa
Chuyển động thẳng biến đổi đều là chuyển động trong đó vận tốc của vật thay đổi đều đặn theo thời gian. Nếu gia tốc không đổi, thì chuyển động là chuyển động thẳng nhanh dần đều hoặc chậm dần đều.
2. Công Thức Cơ Bản
Các công thức quan trọng liên quan đến chuyển động thẳng biến đổi đều bao gồm:
- Gia tốc: \[ a = \frac{\Delta v}{\Delta t} \]
- Quãng đường: \[ s = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 \]
- Vận tốc: \[ v = v_0 + a \cdot t \]
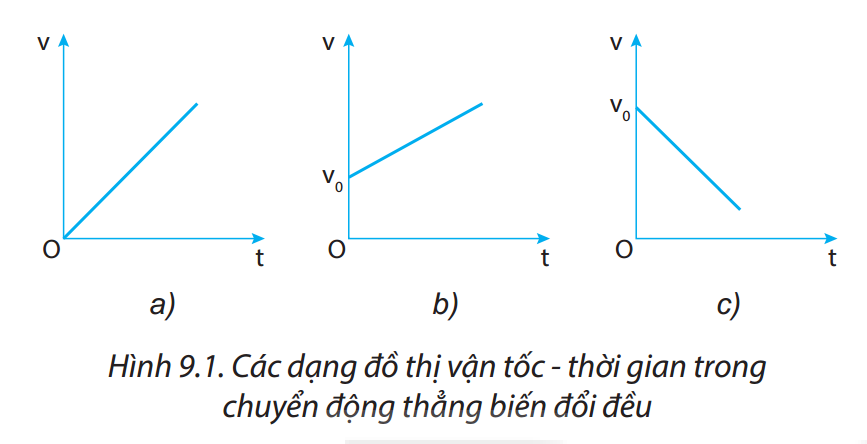
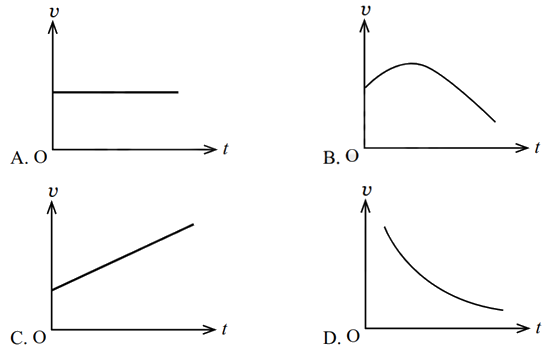
3. Đồ Thị Vận Tốc - Thời Gian
Đồ thị vận tốc - thời gian là một công cụ hữu ích để phân tích chuyển động. Đối với chuyển động thẳng biến đổi đều, đồ thị này là một đường thẳng có độ dốc thể hiện gia tốc của vật.
| Thời gian (t) | Vận tốc (v) |
| 0 | \( v_0 \) |
| t | \( v = v_0 + a \cdot t \) |
4. Bài Tập Vận Dụng
Một số bài tập liên quan đến chuyển động thẳng biến đổi đều thường gặp trong chương trình học:
- Tính quãng đường và vận tốc trung bình của một vật chuyển động thẳng nhanh dần đều.
- Phân tích đồ thị vận tốc - thời gian để xác định các thông số của chuyển động.
- Giải các bài toán liên quan đến gia tốc và vận tốc tức thời.
Chương trình học Vật lý 10 giúp học sinh nắm vững các khái niệm cơ bản về chuyển động, hỗ trợ cho các môn học khác và ứng dụng trong đời sống hàng ngày.

.png)
1. Khái niệm về chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là dạng chuyển động mà vật chuyển động trên quỹ đạo thẳng với gia tốc không đổi. Điều này có nghĩa là vận tốc của vật biến thiên đều theo thời gian, có thể nhanh dần đều hoặc chậm dần đều. Ta có thể biểu diễn gia tốc của chuyển động bằng vectơ \(\vec{a}\), và với chuyển động thẳng biến đổi đều, vectơ gia tốc không thay đổi về độ lớn và hướng.
Công thức tính vận tốc của chuyển động thẳng biến đổi đều được xác định theo thời gian:
Trong đó:
- \(v\): Vận tốc tức thời của vật (m/s)
- \(v_0\): Vận tốc ban đầu (m/s)
- \(a\): Gia tốc của chuyển động (m/s2)
- \(t\): Thời gian chuyển động (s)
Quãng đường đi được trong chuyển động thẳng biến đổi đều được tính theo công thức:
Trong đó:
- \(s\): Quãng đường đi được (m)
- \(v_0\): Vận tốc ban đầu (m/s)
- \(a\): Gia tốc (m/s2)
- \(t\): Thời gian chuyển động (s)
Chuyển động thẳng biến đổi đều thường được phân loại thành hai dạng: chuyển động nhanh dần đều và chuyển động chậm dần đều. Ở chuyển động nhanh dần đều, vận tốc của vật tăng dần theo thời gian. Ngược lại, ở chuyển động chậm dần đều, vận tốc của vật giảm dần đều theo thời gian.
2. Công thức tính gia tốc và quãng đường trong chuyển động thẳng biến đổi đều
Trong chuyển động thẳng biến đổi đều, gia tốc là đại lượng đặc trưng cho sự thay đổi vận tốc theo thời gian. Công thức tính gia tốc được xác định bằng:
\[
a = \frac{\Delta v}{\Delta t}
\]
trong đó \( \Delta v \) là sự thay đổi vận tốc và \( \Delta t \) là khoảng thời gian thay đổi.
Quãng đường mà vật đi được trong chuyển động thẳng biến đổi đều có thể tính bằng công thức:
\[
S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2
\]
với \( v_0 \) là vận tốc ban đầu, \( t \) là thời gian, và \( a \) là gia tốc.
Công thức này giúp tính toán chính xác quãng đường vật di chuyển khi gia tốc không đổi theo thời gian.

3. Đồ thị chuyển động thẳng biến đổi đều
Đồ thị của chuyển động thẳng biến đổi đều là công cụ quan trọng để biểu diễn mối quan hệ giữa các đại lượng vật lý trong quá trình chuyển động. Các đồ thị phổ biến nhất là đồ thị vận tốc - thời gian và đồ thị gia tốc - thời gian.
1. Đồ thị vận tốc - thời gian (v - t)
- Đồ thị là một đường thẳng nghiêng với hệ số góc bằng gia tốc \( a \).
- Nếu chuyển động nhanh dần đều, đồ thị có độ dốc dương.
- Nếu chuyển động chậm dần đều, đồ thị có độ dốc âm.
- Diện tích dưới đường thẳng của đồ thị vận tốc - thời gian cho biết quãng đường đã đi được.
2. Đồ thị gia tốc - thời gian (a - t)
- Đồ thị là một đường thẳng song song với trục thời gian \( t \), cho biết gia tốc không đổi trong suốt quá trình chuyển động.
- Gia tốc dương chỉ ra chuyển động nhanh dần, còn gia tốc âm chỉ ra chuyển động chậm dần.
Việc phân tích các đồ thị này giúp ta hiểu rõ hơn về các đại lượng vật lý và diễn biến của quá trình chuyển động thẳng biến đổi đều.

XEM THÊM:
4. Bài tập minh họa về chuyển động thẳng biến đổi đều
Dưới đây là một số bài tập minh họa về chuyển động thẳng biến đổi đều, giúp củng cố kiến thức đã học và áp dụng công thức vào các tình huống cụ thể:
Bài tập 1: Một xe hơi bắt đầu chuyển động từ trạng thái đứng yên với gia tốc không đổi \( a = 2 \, \text{m/s}^2 \). Tính quãng đường mà xe đi được sau thời gian \( t = 5 \, \text{s} \).
Lời giải:
- Vận tốc ban đầu: \( v_0 = 0 \, \text{m/s} \)
- Gia tốc: \( a = 2 \, \text{m/s}^2 \)
- Thời gian: \( t = 5 \, \text{s} \)
- Quãng đường: \[ S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 = 0 \cdot 5 + \frac{1}{2} \cdot 2 \cdot 5^2 = 25 \, \text{m} \]
Bài tập 2: Một đoàn tàu đang chuyển động với vận tốc \( v = 20 \, \text{m/s} \) và bắt đầu giảm tốc với gia tốc \( a = -2 \, \text{m/s}^2 \). Tính thời gian để đoàn tàu dừng lại hoàn toàn và quãng đường mà nó đi được trước khi dừng lại.
Lời giải:
- Vận tốc ban đầu: \( v_0 = 20 \, \text{m/s} \)
- Gia tốc: \( a = -2 \, \text{m/s}^2 \)
- Thời gian dừng lại: \[ t = \frac{v_0}{|a|} = \frac{20}{2} = 10 \, \text{s} \]
- Quãng đường: \[ S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 = 20 \cdot 10 + \frac{1}{2} \cdot (-2) \cdot 10^2 = 100 \, \text{m} \]
Các bài tập này giúp học sinh nắm vững các khái niệm và công thức liên quan đến chuyển động thẳng biến đổi đều.

5. Luyện tập: Bài tập tự luận và trắc nghiệm
Để củng cố kiến thức về chuyển động thẳng biến đổi đều, dưới đây là một số bài tập tự luận và trắc nghiệm giúp các em học sinh luyện tập và nắm vững các công thức và khái niệm đã học.
Bài tập tự luận
- Một vật bắt đầu chuyển động thẳng nhanh dần đều từ trạng thái đứng yên với gia tốc \( a = 3 \, \text{m/s}^2 \). Sau 10 giây, tính quãng đường mà vật đã đi được và vận tốc tại thời điểm đó.
- Một xe máy đang chuyển động với vận tốc \( v = 15 \, \text{m/s} \) và bắt đầu giảm tốc với gia tốc \( a = -2 \, \text{m/s}^2 \). Tính thời gian để xe dừng lại và quãng đường đi được trước khi dừng.
- Giải thích đồ thị vận tốc - thời gian của một vật chuyển động thẳng biến đổi đều và tính quãng đường từ đồ thị đó.
Bài tập trắc nghiệm
- Câu 1: Khi một vật chuyển động thẳng nhanh dần đều, đại lượng nào dưới đây không đổi?
- A. Vận tốc
- B. Gia tốc
- C. Quãng đường
- D. Thời gian
- Câu 2: Quãng đường mà một vật chuyển động thẳng nhanh dần đều đi được trong khoảng thời gian \( t \) được tính bằng công thức nào?
- A. \( S = v_0 \cdot t + a \cdot t^2 \)
- B. \( S = v_0 + \frac{1}{2} a \cdot t^2 \)
- C. \( S = v_0 \cdot t + \frac{1}{2} a \cdot t^2 \)
- D. \( S = v \cdot t + \frac{1}{2} a \cdot t^2 \)
- Câu 3: Gia tốc của một vật chuyển động thẳng biến đổi đều là bao nhiêu khi vận tốc của nó thay đổi từ 5 m/s lên 15 m/s trong 5 giây?
- A. \( 2 \, \text{m/s}^2 \)
- B. \( 4 \, \text{m/s}^2 \)
- C. \( 1 \, \text{m/s}^2 \)
- D. \( 3 \, \text{m/s}^2 \)
Các bài tập trên không chỉ giúp ôn tập kiến thức lý thuyết mà còn nâng cao khả năng vận dụng vào thực tiễn. Hãy dành thời gian luyện tập để nắm vững hơn về chuyển động thẳng biến đổi đều.