Dạng Bài Tập Chuyển Động Thẳng Biến Đổi Đều: Phân Tích & Hướng Dẫn Giải Chi Tiết

Chuyển động thẳng biến đổi đều là một dạng chuyển động trong đó gia tốc của vật là không đổi. Dưới đây là các dạng bài tập phổ biến và cách giải chi tiết liên quan đến chuyển động thẳng biến đổi đều.

1. Công Thức Cơ Bản

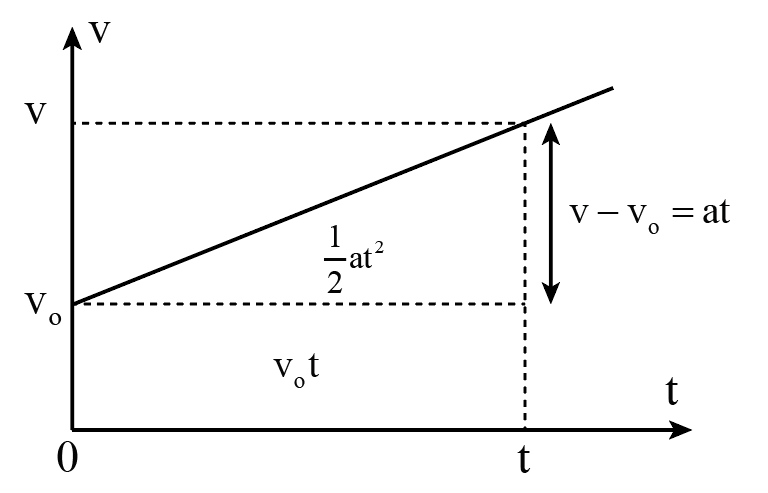
• Công thức tính vận tốc: \( v = v_0 + at \)
• Công thức tính quãng đường: \( s = v_0 t + \frac{1}{2} a t^2 \)
• Công thức liên hệ giữa vận tốc, gia tốc và quãng đường: \( v^2 - v_0^2 = 2as \)

2. Dạng 1: Tính Vận Tốc và Gia Tốc

Ví dụ: Một ô tô đang chạy thẳng đều với tốc độ \( v_0 = 40 \, km/h \). Sau khi tăng ga, ô tô đạt tốc độ \( v = 60 \, km/h \) trên quãng đường \( s = 1 \, km \). Tính gia tốc \( a \) của ô tô.

• Lời giải: Sử dụng công thức \( v^2 - v_0^2 = 2as \) để tính gia tốc \( a \).
• Thay số: \( a = \frac{v^2 - v_0^2}{2s} \).
• Ta có: \( a = \frac{\left(\frac{50}{3}\right)^2 - \left(\frac{100}{9}\right)^2}{2 \times 1000} = 0.077 \, m/s^2 \).

3. Dạng 2: Tính Quãng Đường Chuyển Động

Ví dụ: Một đoàn tàu đang chuyển động với vận tốc \( v_0 = 72 \, km/h \). Khi hãm phanh, tàu chuyển động chậm dần đều và dừng hẳn sau một quãng đường. Tính quãng đường tàu đi được cho đến lúc dừng lại.

• Lời giải: Sử dụng công thức \( v^2 - v_0^2 = 2as \) và \( v = v_0 + at \) để tính quãng đường \( s \).
• Thay số: Tính thời gian dừng lại, sau đó tính quãng đường.

4. Dạng 3: Bài Tập Tổng Hợp

Ví dụ: Một vật chuyển động với gia tốc không đổi \( a = 2 \, m/s^2 \) từ vận tốc ban đầu \( v_0 = 0 \). Tính vận tốc và quãng đường sau \( t = 5 \, s \).

• Lời giải: Áp dụng công thức \( v = v_0 + at \) để tính vận tốc.
• Sau đó, áp dụng công thức \( s = v_0 t + \frac{1}{2} at^2 \) để tính quãng đường.

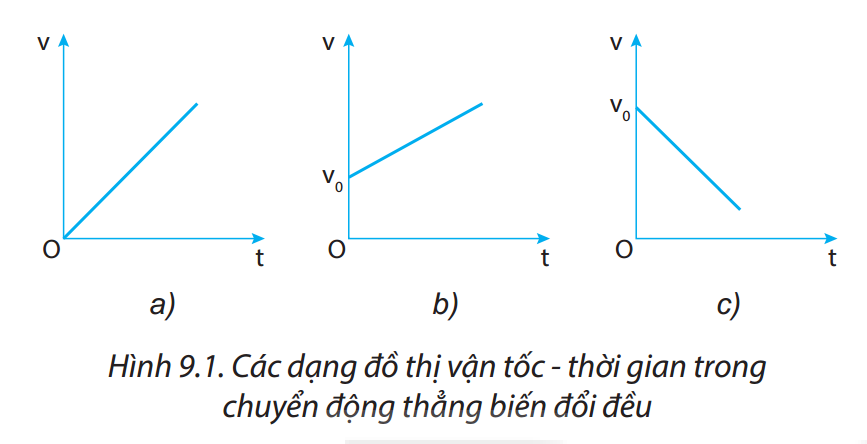
Chuyển động thẳng biến đổi đều là một trong những dạng chuyển động cơ bản trong vật lý, đặc trưng bởi gia tốc không đổi. Trong chuyển động này, vận tốc của vật thay đổi đều theo thời gian, có thể tăng dần hoặc giảm dần tùy theo hướng của gia tốc. Các công thức cơ bản liên quan đến chuyển động thẳng biến đổi đều bao gồm công thức tính vận tốc, gia tốc và quãng đường. Những công thức này giúp xác định các yếu tố chính của chuyển động và đóng vai trò quan trọng trong việc giải các bài tập liên quan.

• Công thức tính vận tốc tại thời điểm \( t \): \( v = v_0 + at \)
• Gia tốc: \( a = \frac{\Delta v}{\Delta t} \)
• Quãng đường đi được: \( s = v_0t + \frac{1}{2}at^2 \)

Trong các bài tập, việc nắm vững các khái niệm này giúp học sinh giải quyết nhanh chóng và chính xác các vấn đề liên quan đến chuyển động thẳng biến đổi đều.

Trong chuyển động thẳng biến đổi đều, các công thức cơ bản giúp xác định các đại lượng như vận tốc, gia tốc, và quãng đường. Dưới đây là các công thức quan trọng mà bạn cần nắm vững:

• Công thức tính vận tốc:

  Vận tốc tại thời điểm \( t \) được tính bằng công thức:

  \[ v = v_0 + at \]

  Trong đó:

  • \( v \): Vận tốc tại thời điểm \( t \)
  • \( v_0 \): Vận tốc ban đầu
  • \( a \): Gia tốc của chuyển động
  • \( t \): Thời gian
• Công thức tính quãng đường:

  Quãng đường đi được trong thời gian \( t \) là:

  \[ s = v_0t + \frac{1}{2}at^2 \]

  Trong đó:

  • \( s \): Quãng đường đi được
  • \( v_0 \): Vận tốc ban đầu
  • \( t \): Thời gian chuyển động
  • \( a \): Gia tốc
• Công thức tính gia tốc:

  Gia tốc được xác định bằng:

  \[ a = \frac{\Delta v}{\Delta t} \]

  Trong đó:

  • \( a \): Gia tốc
  • \( \Delta v \): Độ biến thiên vận tốc
  • \( \Delta t \): Khoảng thời gian biến thiên

Việc áp dụng chính xác các công thức này là yếu tố quan trọng để giải quyết hiệu quả các bài toán liên quan đến chuyển động thẳng biến đổi đều.

Giải các bài tập về chuyển động thẳng biến đổi đều đòi hỏi sự hiểu biết vững chắc về các công thức cơ bản và khả năng áp dụng chúng vào các tình huống cụ thể. Dưới đây là các bước phương pháp giải bài tập một cách hiệu quả:

1. Phân tích đề bài:

   Đọc kỹ đề bài để xác định các dữ liệu cho trước và yêu cầu cần giải quyết. Đánh dấu các thông tin quan trọng như vận tốc ban đầu, gia tốc, thời gian, hoặc quãng đường.

2. Lựa chọn công thức phù hợp:

   Dựa vào các dữ liệu đã xác định, lựa chọn công thức vật lý phù hợp. Các công thức cần sử dụng có thể bao gồm:

   • Công thức vận tốc: \[ v = v_0 + at \]
   • Công thức quãng đường: \[ s = v_0t + \frac{1}{2}at^2 \]
   • Công thức gia tốc: \[ a = \frac{\Delta v}{\Delta t} \]
3. Thực hiện phép tính:

   Thay thế các giá trị số vào công thức đã chọn và thực hiện phép tính cẩn thận. Đảm bảo các đơn vị đo lường được thống nhất để tránh sai sót.

4. Kiểm tra kết quả:

   Sau khi tính toán, hãy kiểm tra lại các bước thực hiện và so sánh kết quả với yêu cầu của đề bài. Đảm bảo kết quả cuối cùng có ý nghĩa thực tế và đúng với các điều kiện của bài toán.

Việc thực hành nhiều dạng bài tập khác nhau và nắm vững phương pháp giải sẽ giúp bạn thành thạo trong việc giải quyết các bài toán liên quan đến chuyển động thẳng biến đổi đều.

Chuyển động thẳng biến đổi đều không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống hàng ngày và các lĩnh vực công nghệ. Dưới đây là một số ứng dụng tiêu biểu:

• Trong giao thông vận tải: Các phương tiện như ô tô, tàu hỏa, và máy bay thường phải sử dụng các nguyên tắc của chuyển động thẳng biến đổi đều để tính toán quãng đường di chuyển, thời gian cần thiết và gia tốc. Ví dụ, khi một chiếc xe hơi bắt đầu tăng tốc từ trạng thái đứng yên, nó sẽ tuân theo quy luật của chuyển động thẳng nhanh dần đều.
• Trong thiết kế và chế tạo máy móc: Các nguyên tắc của chuyển động thẳng biến đổi đều được áp dụng trong việc thiết kế các hệ thống cơ khí, như hệ thống truyền động, để đảm bảo hiệu suất và an toàn khi vận hành.
• Trong nghiên cứu khoa học: Các nhà khoa học sử dụng các phương trình của chuyển động thẳng biến đổi đều để mô tả và dự đoán chuyển động của các vật thể trong không gian, từ đó phát triển các công nghệ vũ trụ như tên lửa và vệ tinh.
• Trong các thiết bị đo lường: Đồng hồ tốc độ trên các phương tiện giao thông là một ứng dụng thực tế của nguyên tắc chuyển động thẳng biến đổi đều, giúp người lái xe biết được vận tốc tức thời của xe.
• Trong công nghệ sản xuất: Các dây chuyền sản xuất tự động sử dụng các nguyên lý của chuyển động thẳng biến đổi đều để điều chỉnh tốc độ di chuyển của sản phẩm, đảm bảo tính đồng nhất và chất lượng của sản phẩm.

Các ứng dụng này không chỉ giúp chúng ta hiểu rõ hơn về nguyên lý vật lý mà còn đóng vai trò quan trọng trong việc phát triển công nghệ và cải thiện chất lượng cuộc sống.

Khi giải bài tập về chuyển động thẳng biến đổi đều, học sinh thường gặp phải một số lỗi phổ biến do hiểu sai khái niệm hoặc áp dụng công thức không đúng cách. Dưới đây là các lỗi thường gặp và cách khắc phục:

5.1. Lỗi sai khi tính gia tốc

• Nhầm lẫn giữa gia tốc và vận tốc: Gia tốc là đại lượng đo sự thay đổi của vận tốc theo thời gian, trong khi vận tốc là đại lượng đo sự thay đổi của quãng đường theo thời gian. Cần chú ý đơn vị và công thức áp dụng.
• Áp dụng sai công thức: Công thức tính gia tốc trong chuyển động thẳng biến đổi đều là: \[ a = \frac{\Delta v}{\Delta t} \] Học sinh thường nhầm lẫn công thức này với công thức tính vận tốc hoặc quãng đường.

5.2. Lỗi sai khi xác định thời gian

• Xác định sai thời gian: Thời gian là đại lượng quan trọng ảnh hưởng đến kết quả tính toán. Học sinh thường tính nhầm thời gian khi không để ý đến các mốc thời gian khác nhau trong bài toán.
• Không chú ý đến thời gian ban đầu: Thời gian trong công thức cần tính từ thời điểm ban đầu, học sinh thường bỏ qua hoặc nhầm lẫn thời điểm này.

5.3. Lỗi sai khi tính toán quãng đường

• Áp dụng sai công thức tính quãng đường: Trong chuyển động thẳng biến đổi đều, công thức tính quãng đường là: \[ s = v_0t + \frac{1}{2}at^2 \] Học sinh thường áp dụng sai công thức, đặc biệt là khi vận tốc ban đầu \(v_0\) khác 0.
• Nhầm lẫn giữa quãng đường và độ dời: Quãng đường là tổng chiều dài của đường đi, trong khi độ dời là khoảng cách ngắn nhất giữa hai điểm. Học sinh thường nhầm lẫn giữa hai khái niệm này.