Chuyển Động Thẳng Biến Đổi Đều: Khám Phá Toàn Diện và Ứng Dụng Thực Tiễn

Chuyển động thẳng biến đổi đều là một khái niệm cơ bản trong Vật lý, thường được giới thiệu trong chương trình học trung học phổ thông. Đây là loại chuyển động trong đó vận tốc của vật thay đổi đều theo thời gian. Dưới đây là những nội dung chi tiết về chuyển động thẳng biến đổi đều:

1. Khái Niệm Cơ Bản

Chuyển động thẳng biến đổi đều được chia làm hai loại chính:

• Chuyển động thẳng nhanh dần đều: Là chuyển động mà vận tốc của vật tăng đều theo thời gian, gia tốc \(a > 0\).
• Chuyển động thẳng chậm dần đều: Là chuyển động mà vận tốc của vật giảm đều theo thời gian, gia tốc \(a < 0\).

2. Các Công Thức Cơ Bản

• Gia tốc: \[ a = \frac{v - v_0}{t} \] trong đó:
  • \(v_0\): Vận tốc ban đầu (m/s)
  • \(v\): Vận tốc sau một khoảng thời gian \(t\) (m/s)
  • \(t\): Thời gian (s)
• Phương trình vận tốc: \[ v = v_0 + at \]
• Phương trình tọa độ: \[ x = x_0 + v_0t + \frac{1}{2}at^2 \] trong đó:
  • \(x_0\): Tọa độ ban đầu (m)
  • \(x\): Tọa độ sau một khoảng thời gian \(t\) (m)
• Phương trình liên hệ giữa gia tốc, vận tốc và quãng đường: \[ v^2 - v_0^2 = 2a(x - x_0) \]

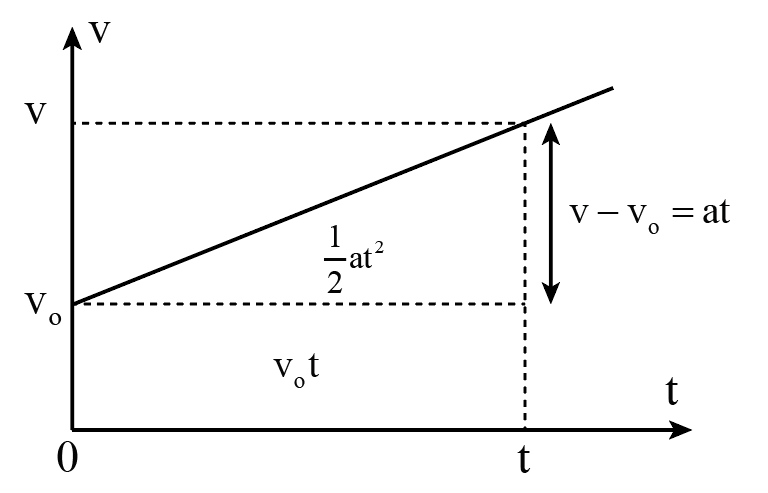
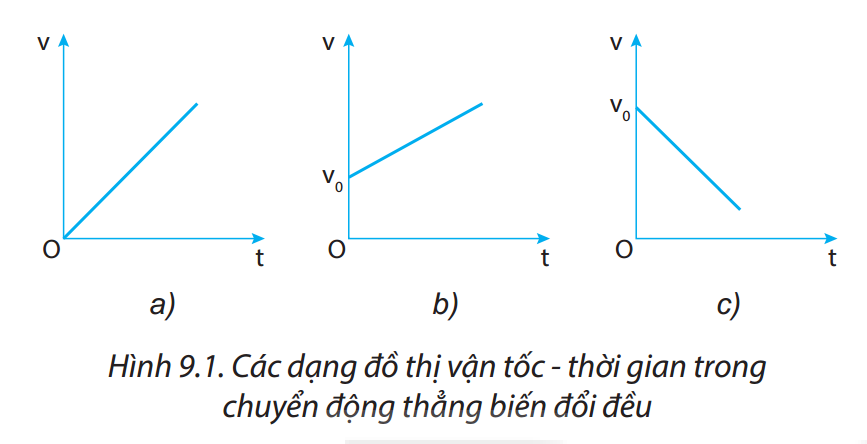
3. Đồ Thị Chuyển Động

Đồ thị trong chuyển động thẳng biến đổi đều thường được vẽ theo các dạng:

• Đồ thị vận tốc - thời gian (v - t): Là một đường thẳng nghiêng, với độ dốc là gia tốc \(a\).
• Đồ thị tọa độ - thời gian (x - t): Là một parabol, biểu diễn sự thay đổi của tọa độ theo thời gian.

4. Bài Tập Thực Hành

Dưới đây là một số bài tập thường gặp liên quan đến chuyển động thẳng biến đổi đều:

1. Một ô tô bắt đầu chuyển động thẳng nhanh dần đều với gia tốc \(a = 2 \, m/s^2\). Tính vận tốc của ô tô sau 5 giây.
2. Một viên bi được thả lăn xuống một mặt phẳng nghiêng, chuyển động thẳng nhanh dần đều. Tính quãng đường viên bi đi được trong 3 giây đầu tiên.
3. Một đoàn tàu chuyển động thẳng chậm dần đều, với vận tốc ban đầu là 20 m/s và gia tốc \(a = -1 \, m/s^2\). Sau bao lâu tàu sẽ dừng lại?

5. Ứng Dụng Thực Tế

Chuyển động thẳng biến đổi đều có nhiều ứng dụng trong thực tế, như trong việc thiết kế đường ray tàu hỏa, đường băng sân bay, và trong các bài toán tính toán trong ngành cơ khí và kỹ thuật.

Chuyển động thẳng biến đổi đều là một trong những khái niệm cơ bản của cơ học trong Vật lý, liên quan đến sự thay đổi đều đặn của vận tốc theo thời gian trong một đường thẳng. Đây là một trong những loại chuyển động thường gặp và có ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật.

Trong chuyển động thẳng biến đổi đều, có hai trường hợp chính:

• Chuyển động thẳng nhanh dần đều: Đây là loại chuyển động mà vận tốc của vật tăng đều theo thời gian, với gia tốc \(a > 0\). Gia tốc trong trường hợp này là dương, biểu thị sự tăng tốc của vật.
• Chuyển động thẳng chậm dần đều: Đây là loại chuyển động mà vận tốc của vật giảm đều theo thời gian, với gia tốc \(a < 0\). Gia tốc trong trường hợp này là âm, biểu thị sự giảm tốc của vật.

Các công thức cơ bản liên quan đến chuyển động thẳng biến đổi đều bao gồm:

• Vận tốc: \[ v = v_0 + at \] trong đó:
  • \(v\) là vận tốc của vật tại thời điểm \(t\)
  • \(v_0\) là vận tốc ban đầu
  • \(a\) là gia tốc
  • \(t\) là thời gian
• Phương trình quãng đường: \[ s = v_0t + \frac{1}{2}at^2 \]
• Phương trình liên hệ giữa vận tốc và quãng đường: \[ v^2 = v_0^2 + 2as \]

Những phương trình trên giúp xác định các thông số chuyển động như vận tốc, quãng đường và thời gian khi biết một số yếu tố còn lại. Chuyển động thẳng biến đổi đều được mô tả bởi các đồ thị như đồ thị vận tốc - thời gian (v-t) và đồ thị tọa độ - thời gian (x-t), giúp minh họa trực quan sự biến đổi của vận tốc và vị trí của vật theo thời gian.

Trong chuyển động thẳng biến đổi đều, các công thức và phương trình cơ bản giúp chúng ta xác định các yếu tố quan trọng như vận tốc, quãng đường và thời gian. Dưới đây là những công thức cần thiết trong việc giải quyết các bài toán liên quan:

2.1 Công Thức Tính Vận Tốc

Vận tốc trong chuyển động thẳng biến đổi đều được tính bằng công thức:

• \(v\) là vận tốc của vật tại thời điểm \(t\).
• \(v_0\) là vận tốc ban đầu của vật.
• \(a\) là gia tốc (với \(a > 0\) là chuyển động nhanh dần đều, và \(a < 0\) là chuyển động chậm dần đều).
• \(t\) là thời gian đã trôi qua.

2.2 Công Thức Tính Quãng Đường

Quãng đường mà vật đi được trong chuyển động thẳng biến đổi đều được xác định bằng công thức:

• \(s\) là quãng đường vật đi được.
• \(v_0\) là vận tốc ban đầu của vật.
• \(a\) là gia tốc của vật.
• \(t\) là thời gian chuyển động.

2.3 Phương Trình Liên Hệ Giữa Vận Tốc và Quãng Đường

Phương trình này giúp liên hệ giữa vận tốc, gia tốc và quãng đường đi được của vật:

• \(v\) là vận tốc tại thời điểm đang xét.
• \(v_0\) là vận tốc ban đầu.
• \(a\) là gia tốc của vật.
• \(s\) là quãng đường đi được.

Các phương trình trên là nền tảng để giải các bài toán liên quan đến chuyển động thẳng biến đổi đều, giúp chúng ta xác định chính xác các yếu tố như vận tốc, quãng đường, và thời gian trong các tình huống thực tế.

Đồ thị là công cụ trực quan giúp minh họa sự biến đổi của các đại lượng vật lý trong chuyển động thẳng biến đổi đều. Có hai loại đồ thị chính thường được sử dụng để phân tích chuyển động này: đồ thị vận tốc - thời gian (v-t) và đồ thị tọa độ - thời gian (x-t).

3.1 Đồ Thị Vận Tốc - Thời Gian (v-t)

Đồ thị vận tốc - thời gian (v-t) là một đường thẳng biểu diễn mối quan hệ giữa vận tốc của vật và thời gian:

• Nếu chuyển động là nhanh dần đều (\(a > 0\)), đồ thị là một đường thẳng đi lên với độ dốc dương, biểu thị vận tốc tăng theo thời gian.
• Nếu chuyển động là chậm dần đều (\(a < 0\)), đồ thị là một đường thẳng đi xuống với độ dốc âm, biểu thị vận tốc giảm theo thời gian.
• Diện tích dưới đường thẳng trong đồ thị này biểu thị quãng đường đi được của vật trong khoảng thời gian xét.

Trong đó:

• \(v\): vận tốc tại thời điểm đang xét
• \(v_0\): vận tốc ban đầu
• \(a\): gia tốc
• \(t\): thời gian

3.2 Đồ Thị Tọa Độ - Thời Gian (x-t)

Đồ thị tọa độ - thời gian (x-t) cho biết sự thay đổi của vị trí vật theo thời gian. Đồ thị này có dạng parabol nếu gia tốc không bằng 0:

• Nếu chuyển động là nhanh dần đều, đồ thị là một parabol hướng lên, biểu thị quãng đường tăng nhanh theo thời gian.
• Nếu chuyển động là chậm dần đều, đồ thị là một parabol hướng xuống, biểu thị quãng đường giảm dần theo thời gian.

Trong đó:

• \(x\): tọa độ tại thời điểm đang xét
• \(x_0\): tọa độ ban đầu
• \(v_0\): vận tốc ban đầu
• \(a\): gia tốc
• \(t\): thời gian

Đồ thị (x-t) giúp ta hiểu rõ hơn về sự biến đổi vị trí của vật trong suốt quá trình chuyển động, đặc biệt hữu ích khi phân tích các bài toán phức tạp.

Để giải các bài tập liên quan đến chuyển động thẳng biến đổi đều, cần nắm vững các công thức cơ bản và áp dụng chúng một cách linh hoạt. Dưới đây là phương pháp giải bài tập theo từng bước chi tiết.

4.1 Xác Định Các Đại Lượng Đã Cho và Cần Tìm

Trước tiên, hãy đọc kỹ đề bài và xác định các thông số đã cho như vận tốc ban đầu \(v_0\), gia tốc \(a\), thời gian \(t\), và quãng đường \(s\). Ghi lại những đại lượng cần tìm.

4.2 Chọn Công Thức Phù Hợp

Dựa trên các đại lượng đã biết, chọn công thức phù hợp để giải bài toán. Các công thức thường được sử dụng bao gồm:

• Công thức tính vận tốc: \[ v = v_0 + at \]
• Công thức tính quãng đường: \[ s = v_0t + \frac{1}{2}at^2 \]
• Phương trình liên hệ giữa vận tốc và quãng đường: \[ v^2 = v_0^2 + 2as \]

4.3 Giải Quyết Bài Toán

Thay các giá trị đã cho vào công thức và tính toán để tìm ra kết quả. Hãy chắc chắn kiểm tra lại đơn vị của các đại lượng để đảm bảo tính chính xác.

4.4 Kiểm Tra và Xác Nhận Kết Quả

Sau khi tính toán, hãy kiểm tra lại kết quả bằng cách xét xem nó có hợp lý với tình huống thực tế của bài toán hay không. Điều này giúp tránh những sai lầm có thể xảy ra trong quá trình tính toán.

4.5 Thực Hành Với Nhiều Dạng Bài Tập

Để nắm vững kiến thức, cần thực hành với nhiều dạng bài tập khác nhau, từ cơ bản đến nâng cao. Việc này giúp củng cố kỹ năng và tăng khả năng ứng dụng các công thức một cách linh hoạt trong các tình huống khác nhau.

Chuyển động thẳng biến đổi đều không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế trong cuộc sống. Những nguyên lý của nó được áp dụng trong nhiều lĩnh vực khác nhau, từ giao thông vận tải đến kỹ thuật và công nghiệp.

5.1 Trong Giao Thông Vận Tải

Chuyển động thẳng biến đổi đều là cơ sở để thiết kế hệ thống phanh và tăng tốc của các phương tiện giao thông như ô tô, tàu hỏa, và máy bay. Việc tính toán chính xác gia tốc và quãng đường cần thiết để dừng lại hoặc đạt đến một vận tốc nhất định giúp đảm bảo an toàn giao thông.

5.2 Trong Kỹ Thuật Cơ Khí

Trong lĩnh vực kỹ thuật cơ khí, nguyên lý của chuyển động thẳng biến đổi đều được áp dụng để thiết kế các hệ thống chuyển động, như băng tải tự động trong nhà máy. Các công thức liên quan đến gia tốc và quãng đường giúp kỹ sư tính toán chính xác các yếu tố cần thiết để hệ thống hoạt động hiệu quả.

5.3 Trong Công Nghiệp Sản Xuất

Các dây chuyền sản xuất sử dụng chuyển động thẳng biến đổi đều để di chuyển sản phẩm qua các giai đoạn khác nhau một cách hiệu quả. Việc điều chỉnh tốc độ chuyển động của băng chuyền theo yêu cầu sản xuất giúp tối ưu hóa năng suất và giảm thiểu lãng phí.

5.4 Trong Khoa Học Vũ Trụ

Chuyển động thẳng biến đổi đều được ứng dụng trong việc tính toán đường bay và vận tốc của các tàu vũ trụ khi chúng rời khỏi hoặc trở về Trái Đất. Việc áp dụng đúng nguyên lý này giúp đảm bảo an toàn và chính xác trong các nhiệm vụ không gian.

5.5 Trong Thiết Kế Đô Thị

Nguyên lý của chuyển động thẳng biến đổi đều được áp dụng trong việc thiết kế các hệ thống đường phố và đèn giao thông. Việc tính toán đúng gia tốc và vận tốc của phương tiện giúp tối ưu hóa lưu thông và giảm ùn tắc giao thông trong các khu vực đô thị.

Khi học về chuyển động thẳng biến đổi đều, đặc biệt là trong việc ứng dụng vào các bài tập và thực tế, có một số điểm cần lưu ý để tránh những sai lầm phổ biến và tối ưu hóa quá trình học tập.

6.1 Sai lầm thường gặp

• Xác định sai dấu của gia tốc: Trong chuyển động thẳng nhanh dần đều, gia tốc có dấu cùng với vận tốc, ngược lại trong chuyển động thẳng chậm dần đều, gia tốc có dấu ngược với vận tốc. Việc xác định sai dấu của gia tốc sẽ dẫn đến các kết quả tính toán sai.
• Không chú ý đến đơn vị: Quên đổi đơn vị khi tính toán giữa các đại lượng như quãng đường, thời gian, vận tốc và gia tốc là một trong những sai lầm phổ biến, dẫn đến kết quả không chính xác.
• Sử dụng sai công thức: Mỗi công thức đều có phạm vi áp dụng riêng, như công thức tính quãng đường chỉ áp dụng cho chuyển động thẳng biến đổi đều. Việc áp dụng sai công thức trong các trường hợp khác sẽ dẫn đến kết quả sai lầm.

6.2 Kinh nghiệm học tập và thực hành

1. Luyện tập với nhiều bài tập đa dạng: Thực hành nhiều dạng bài tập khác nhau sẽ giúp bạn nắm vững các công thức và cách áp dụng chúng trong các tình huống cụ thể.
2. Sử dụng đồ thị: Đồ thị vận tốc-thời gian và tọa độ-thời gian là công cụ hữu ích để hình dung và phân tích chuyển động. Thường xuyên vẽ và phân tích đồ thị sẽ giúp bạn hiểu sâu hơn về bản chất của chuyển động thẳng biến đổi đều.
3. Nhớ rõ các công thức liên quan: Các công thức tính vận tốc, quãng đường và gia tốc có mối liên hệ chặt chẽ với nhau. Sử dụng MathJax để ghi nhớ các công thức: \[ v = v_0 + a t \] \[ s = v_0 t + \frac{1}{2} a t^2 \] \[ v^2 = v_0^2 + 2a s \] Việc hiểu rõ cách dẫn dắt và biến đổi công thức sẽ giúp bạn ứng dụng chính xác vào bài tập.
4. Ứng dụng thực tế: Quan sát các hiện tượng chuyển động trong đời sống hàng ngày như xe cộ chuyển động, máy móc hoạt động sẽ giúp bạn liên hệ lý thuyết với thực tế, từ đó hiểu bài học sâu sắc hơn.