Chủ đề vận tốc của chuyển động thẳng biến đổi đều: Vận tốc của chuyển động thẳng biến đổi đều là một chủ đề quan trọng trong vật lý học, liên quan mật thiết đến các bài toán về chuyển động. Bài viết này sẽ giúp bạn hiểu rõ khái niệm, cách tính vận tốc, và các ứng dụng thực tiễn của chuyển động thẳng biến đổi đều trong đời sống.
Mục lục
Vận tốc của chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là một dạng chuyển động thẳng mà trong đó vận tốc của vật thay đổi đều theo thời gian. Đây là một khái niệm cơ bản trong vật lý học và thường được áp dụng trong nhiều bài toán chuyển động cơ bản.
Khái niệm và định nghĩa
Vận tốc của chuyển động thẳng biến đổi đều là đại lượng vector có độ lớn thay đổi đều đặn theo thời gian. Độ lớn của vận tốc có thể tăng dần hoặc giảm dần tùy thuộc vào gia tốc của vật.
- Vận tốc tức thời: Vận tốc tại một thời điểm nhất định.
- Vận tốc trung bình: Tỷ số giữa quãng đường đi được và khoảng thời gian di chuyển.
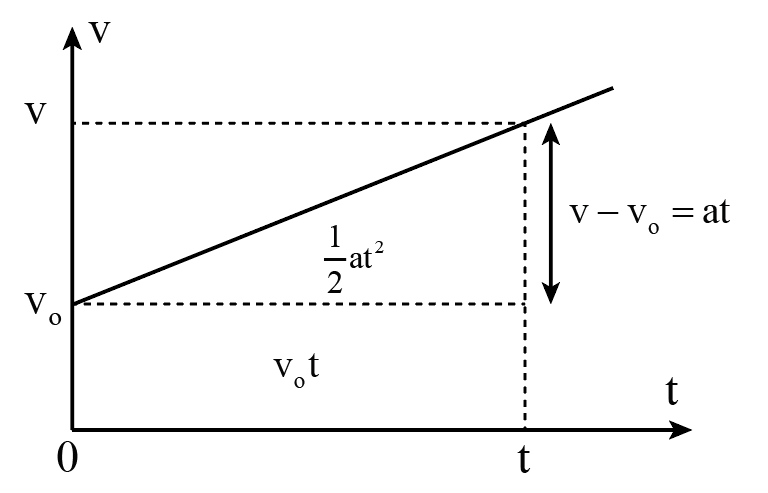
Trong chuyển động thẳng biến đổi đều, vận tốc tức thời \(v\) tại thời điểm \(t\) được xác định theo công thức:
\[
v = v_0 + at
\]
Trong đó:
- \(v_0\): Vận tốc ban đầu (tại thời điểm \(t = 0\)).
- \(a\): Gia tốc của chuyển động, có thể là dương (tăng tốc) hoặc âm (giảm tốc).
- \(t\): Thời gian kể từ thời điểm bắt đầu chuyển động.
Ứng dụng của vận tốc trong chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều thường được sử dụng để mô tả các hiện tượng trong thực tế như:
- Xe chuyển động tăng tốc đều khi xuất phát từ trạng thái đứng yên.
- Vật rơi tự do dưới tác động của trọng lực (nếu bỏ qua lực cản không khí).
Khi áp dụng công thức tính vận tốc vào các bài toán thực tế, chúng ta có thể dễ dàng xác định được các thông số quan trọng như vận tốc tại một thời điểm cụ thể hoặc quãng đường mà vật đã di chuyển sau một khoảng thời gian nhất định.
Tổng kết
Vận tốc của chuyển động thẳng biến đổi đều là một khái niệm cơ bản nhưng quan trọng trong vật lý học. Nắm vững các công thức và ứng dụng của vận tốc sẽ giúp giải quyết nhiều bài toán trong thực tế cũng như trong các kỳ thi học thuật.

.png)
1. Khái niệm và định nghĩa
Chuyển động thẳng biến đổi đều là một dạng chuyển động cơ bản trong vật lý, trong đó một vật di chuyển theo đường thẳng với vận tốc thay đổi đều theo thời gian. Đây là trường hợp quan trọng trong việc nghiên cứu các quy luật chuyển động của vật thể.
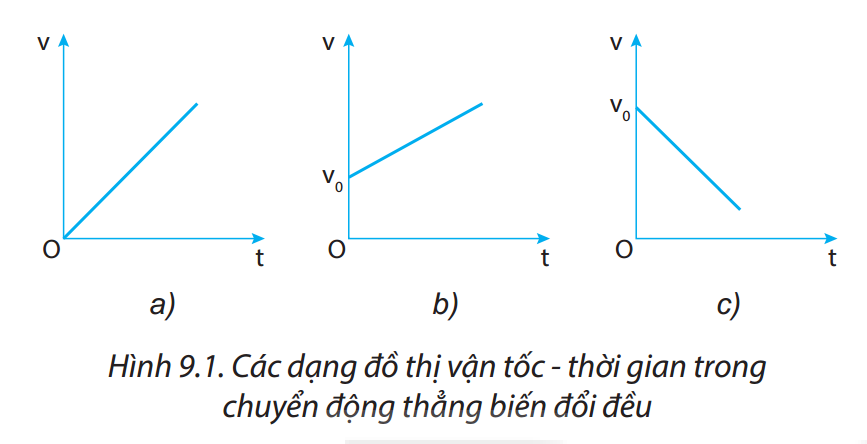
Trong chuyển động thẳng biến đổi đều, vận tốc của vật có thể thay đổi theo hai hướng:
- Gia tốc dương (tăng tốc): Vận tốc của vật tăng đều theo thời gian.
- Gia tốc âm (giảm tốc): Vận tốc của vật giảm đều theo thời gian.
Vận tốc của vật tại một thời điểm bất kỳ trong chuyển động thẳng biến đổi đều được xác định bằng công thức:
\[
v = v_0 + at
\]
Trong đó:
- \(v\): Vận tốc của vật tại thời điểm \(t\).
- \(v_0\): Vận tốc ban đầu của vật (tại thời điểm \(t = 0\)).
- \(a\): Gia tốc của vật.
- \(t\): Thời gian kể từ thời điểm bắt đầu chuyển động.
Đặc điểm quan trọng của chuyển động thẳng biến đổi đều là gia tốc \(a\) không đổi. Điều này có nghĩa là sự thay đổi vận tốc theo thời gian là tuyến tính, tạo điều kiện thuận lợi cho việc phân tích và giải các bài toán liên quan đến chuyển động.
Tóm lại, khái niệm chuyển động thẳng biến đổi đều mô tả một dạng chuyển động trong đó vận tốc của vật thay đổi đều theo thời gian, và gia tốc của vật luôn không đổi.
2. Công thức tính vận tốc trong chuyển động thẳng biến đổi đều
Trong chuyển động thẳng biến đổi đều, vận tốc của vật thay đổi đều đặn theo thời gian, và gia tốc là một hằng số. Dưới đây là các công thức cơ bản để tính vận tốc trong các trường hợp khác nhau của chuyển động này.
2.1. Công thức tính vận tốc tức thời
Vận tốc tức thời của vật tại một thời điểm bất kỳ \(t\) trong chuyển động thẳng biến đổi đều được xác định theo công thức:
\[
v = v_0 + at
\]
Trong đó:
- \(v\): Vận tốc tức thời của vật tại thời điểm \(t\).
- \(v_0\): Vận tốc ban đầu của vật (tại thời điểm \(t = 0\)).
- \(a\): Gia tốc của vật, là đại lượng không đổi.
- \(t\): Thời gian kể từ lúc bắt đầu chuyển động.
2.2. Công thức tính vận tốc trung bình
Vận tốc trung bình trong chuyển động thẳng biến đổi đều là giá trị trung bình của vận tốc ban đầu và vận tốc tức thời tại thời điểm kết thúc. Công thức được cho bởi:
\[
v_{tb} = \frac{v_0 + v}{2}
\]
Trong đó:
- \(v_{tb}\): Vận tốc trung bình.
- \(v_0\): Vận tốc ban đầu của vật.
- \(v\): Vận tốc tại thời điểm bất kỳ \(t\).
2.3. Mối quan hệ giữa vận tốc, gia tốc và quãng đường
Vận tốc cũng có thể được liên hệ với quãng đường \(s\) mà vật đã di chuyển trong thời gian \(t\) theo công thức:
\[
v^2 = v_0^2 + 2as
\]
Trong đó:
- \(v\): Vận tốc tức thời của vật.
- \(v_0\): Vận tốc ban đầu của vật.
- \(a\): Gia tốc của vật.
- \(s\): Quãng đường mà vật đã di chuyển.
Các công thức trên là cơ sở để giải các bài toán liên quan đến chuyển động thẳng biến đổi đều, giúp xác định vận tốc, thời gian, và quãng đường trong các tình huống khác nhau.

3. Ứng dụng thực tiễn của chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là một khái niệm cơ bản trong vật lý, nhưng nó có rất nhiều ứng dụng trong thực tiễn. Dưới đây là một số ví dụ điển hình về cách chuyển động thẳng biến đổi đều được áp dụng trong cuộc sống hàng ngày và trong các ngành khoa học kỹ thuật.
3.1. Chuyển động của xe cộ trên đường
Trong thực tế, khi một chiếc xe tăng tốc hoặc giảm tốc một cách đều đặn, nó đang thực hiện chuyển động thẳng biến đổi đều. Ví dụ, khi một chiếc ô tô tăng tốc từ trạng thái đứng yên với một gia tốc không đổi, ta có thể áp dụng công thức của chuyển động thẳng biến đổi đều để tính vận tốc của xe tại một thời điểm bất kỳ hoặc quãng đường mà xe đã đi được.
3.2. Vật rơi tự do
Khi một vật rơi tự do trong điều kiện không có lực cản của không khí, nó sẽ thực hiện chuyển động thẳng biến đổi đều với gia tốc là gia tốc trọng trường \(g\). Chúng ta có thể sử dụng các công thức chuyển động thẳng biến đổi đều để xác định vận tốc của vật tại các thời điểm khác nhau cũng như quãng đường mà nó rơi.
3.3. Các bài toán trong kỹ thuật và công nghiệp
Trong ngành công nghiệp và kỹ thuật, nhiều loại máy móc và thiết bị hoạt động dựa trên nguyên lý của chuyển động thẳng biến đổi đều. Ví dụ, băng chuyền trong các nhà máy có thể được thiết kế để tăng tốc hoặc giảm tốc đều, giúp vận chuyển sản phẩm một cách hiệu quả và an toàn.
3.4. Tính toán đường đi trong thể thao
Trong một số môn thể thao, như điền kinh hoặc đua xe, vận động viên hoặc xe đua có thể tăng tốc đều để đạt được vận tốc tối đa. Sử dụng kiến thức về chuyển động thẳng biến đổi đều, các huấn luyện viên và nhà phân tích có thể dự đoán hiệu suất của vận động viên hoặc xe đua và đưa ra các chiến lược tối ưu.
3.5. Phân tích tai nạn giao thông
Chuyển động thẳng biến đổi đều cũng được sử dụng trong việc phân tích các vụ tai nạn giao thông. Bằng cách sử dụng các công thức liên quan, các chuyên gia có thể xác định tốc độ của xe tại thời điểm xảy ra va chạm, từ đó giúp xác định nguyên nhân và trách nhiệm trong các vụ tai nạn.
Như vậy, chuyển động thẳng biến đổi đều không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn, đóng vai trò quan trọng trong nhiều lĩnh vực của cuộc sống.

4. Bài tập vận dụng về vận tốc của chuyển động thẳng biến đổi đều
Để nắm vững kiến thức về vận tốc trong chuyển động thẳng biến đổi đều, việc luyện tập thông qua các bài tập là vô cùng cần thiết. Dưới đây là một số bài tập cơ bản và nâng cao kèm theo hướng dẫn chi tiết để giúp bạn áp dụng các công thức và khái niệm đã học.
4.1. Bài tập cơ bản
Một ô tô bắt đầu chuyển động từ trạng thái đứng yên với gia tốc \(a = 2 \, m/s^2\). Hãy tính vận tốc của ô tô sau 5 giây kể từ khi bắt đầu chuyển động.
Lời giải: Sử dụng công thức:
\[
v = v_0 + at
\]Với \(v_0 = 0\), \(a = 2 \, m/s^2\), \(t = 5 \, s\), ta có:
\[
v = 0 + 2 \times 5 = 10 \, m/s
\]Vậy vận tốc của ô tô sau 5 giây là 10 m/s.
Một vật chuyển động thẳng biến đổi đều với vận tốc ban đầu \(v_0 = 3 \, m/s\) và gia tốc \(a = 1 \, m/s^2\). Tính vận tốc của vật sau khi nó đi được quãng đường 10 m.
Lời giải: Sử dụng công thức:
\[
v^2 = v_0^2 + 2as
\]Với \(v_0 = 3 \, m/s\), \(a = 1 \, m/s^2\), \(s = 10 \, m\), ta có:
\[
v^2 = 3^2 + 2 \times 1 \times 10 = 9 + 20 = 29
\]Vậy:
\[
v = \sqrt{29} \approx 5.39 \, m/s
\]Vận tốc của vật sau khi đi được quãng đường 10 m là khoảng 5.39 m/s.
4.2. Bài tập nâng cao
Một xe buýt đang di chuyển với vận tốc \(v = 15 \, m/s\) thì tài xế bắt đầu giảm tốc với gia tốc \(-2 \, m/s^2\). Hỏi sau bao lâu xe buýt sẽ dừng lại hoàn toàn?
Lời giải: Sử dụng công thức:
\[
v = v_0 + at
\]Với \(v = 0\), \(v_0 = 15 \, m/s\), \(a = -2 \, m/s^2\), ta có:
\[
0 = 15 - 2t \implies t = \frac{15}{2} = 7.5 \, s
\]Vậy xe buýt sẽ dừng lại hoàn toàn sau 7.5 giây.
Một vật bắt đầu chuyển động từ điểm A với vận tốc \(v_0 = 5 \, m/s\) và gia tốc \(a = 3 \, m/s^2\). Sau 4 giây, tính vận tốc và quãng đường vật đi được.
Lời giải:
Vận tốc sau 4 giây được tính bằng công thức:
\[
v = v_0 + at = 5 + 3 \times 4 = 17 \, m/s
\]Quãng đường đi được sau 4 giây là:
\[
s = v_0t + \frac{1}{2}at^2 = 5 \times 4 + \frac{1}{2} \times 3 \times 4^2 = 20 + 24 = 44 \, m
\]Vậy vận tốc của vật sau 4 giây là 17 m/s và quãng đường vật đi được là 44 m.
4.3. Lời giải và hướng dẫn chi tiết
Các bài tập trên là những ví dụ điển hình để áp dụng các công thức tính vận tốc trong chuyển động thẳng biến đổi đều. Khi giải các bài tập, cần chú ý đến đơn vị đo lường, xác định đúng các giá trị ban đầu và áp dụng công thức một cách chính xác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và áp dụng chúng một cách hiệu quả.

5. Tổng kết và lưu ý
Qua các phần đã trình bày, chúng ta đã tìm hiểu chi tiết về vận tốc trong chuyển động thẳng biến đổi đều, từ khái niệm, công thức tính toán, ứng dụng thực tiễn cho đến bài tập vận dụng. Dưới đây là những điểm tổng kết và một số lưu ý quan trọng khi học và áp dụng kiến thức này.
5.1. Tổng kết
- Chuyển động thẳng biến đổi đều là một loại chuyển động mà vận tốc thay đổi đều theo thời gian, với gia tốc là hằng số.
- Các công thức cơ bản liên quan đến vận tốc trong chuyển động này bao gồm công thức tính vận tốc tức thời, vận tốc trung bình, và mối quan hệ giữa vận tốc, gia tốc và quãng đường.
- Chuyển động thẳng biến đổi đều có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật, chẳng hạn như trong việc mô phỏng chuyển động của xe cộ, vật rơi tự do, hay trong thiết kế máy móc công nghiệp.
- Bài tập vận dụng giúp củng cố kiến thức và khả năng áp dụng các công thức vào các tình huống cụ thể, từ đó nâng cao khả năng giải quyết vấn đề.
5.2. Lưu ý quan trọng
- Khi giải các bài toán liên quan đến chuyển động thẳng biến đổi đều, hãy chú ý đến đơn vị của các đại lượng và đảm bảo chúng phù hợp trong quá trình tính toán.
- Gia tốc trong chuyển động thẳng biến đổi đều có thể là dương (tăng tốc) hoặc âm (giảm tốc). Việc xác định đúng dấu của gia tốc là rất quan trọng để áp dụng chính xác các công thức.
- Luôn kiểm tra kỹ lưỡng các giá trị đầu vào và điều kiện bài toán trước khi bắt đầu giải để tránh sai sót.
- Thực hành thường xuyên với các bài tập đa dạng sẽ giúp bạn nắm vững và sử dụng thành thạo các công thức, đồng thời phát triển tư duy logic và kỹ năng giải quyết vấn đề.
Vận tốc trong chuyển động thẳng biến đổi đều là một chủ đề quan trọng không chỉ trong vật lý mà còn trong nhiều lĩnh vực khác của cuộc sống. Hiểu và áp dụng thành thạo kiến thức này sẽ giúp bạn không chỉ trong học tập mà còn trong các ứng dụng thực tiễn.