Chủ đề trong chuyển động thẳng đều thì gia tốc: Trong chuyển động thẳng đều, gia tốc đóng vai trò quan trọng trong việc hiểu rõ về sự vận động của các đối tượng. Bài viết này sẽ giải thích khái niệm gia tốc trong chuyển động thẳng đều, lý do tại sao gia tốc bằng 0, và cung cấp các công thức cũng như ví dụ cụ thể để bạn dễ dàng nắm bắt và áp dụng trong thực tế.
Mục lục
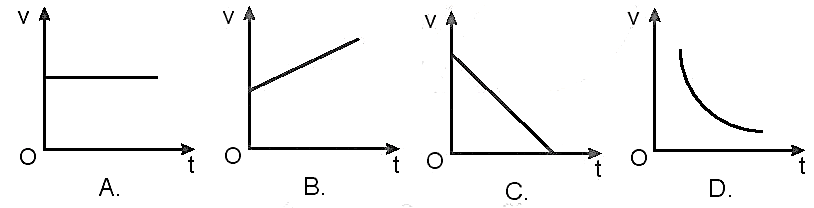
Chuyển Động Thẳng Đều và Gia Tốc
Trong vật lý, chuyển động thẳng đều là một loại chuyển động có quỹ đạo thẳng, trong đó vận tốc của vật là không đổi theo thời gian. Đây là một khái niệm cơ bản trong cơ học cổ điển và có ứng dụng rộng rãi trong cuộc sống hàng ngày cũng như trong nhiều lĩnh vực nghiên cứu khoa học.
Đặc Điểm Của Chuyển Động Thẳng Đều
- Quỹ đạo là đường thẳng.
- Vận tốc có độ lớn và hướng không đổi.
- Gia tốc bằng 0, tức là vật không có sự thay đổi về vận tốc theo thời gian.
Công thức xác định vận tốc trong chuyển động thẳng đều:
Trong đó:
- v: vận tốc (m/s).
- s: quãng đường đi được (m).
- t: thời gian (s).
Gia Tốc Trong Chuyển Động Thẳng Đều
Trong chuyển động thẳng đều, vì vận tốc không thay đổi theo thời gian, nên gia tốc của vật bằng 0. Điều này có nghĩa là không có lực nào tác động để thay đổi trạng thái chuyển động của vật.
Công thức gia tốc:
Trong chuyển động thẳng đều:
Vì không có sự thay đổi vận tốc (\(\Delta v = 0\)), nên gia tốc luôn bằng 0.
Ví Dụ Về Chuyển Động Thẳng Đều
- Một chiếc ô tô chạy trên đường thẳng với tốc độ không đổi.
- Một đoàn tàu chạy đều trên đường ray mà không thay đổi vận tốc.
Ứng Dụng Của Chuyển Động Thẳng Đều
Chuyển động thẳng đều có nhiều ứng dụng trong đời sống và công nghệ:
- Trong giao thông vận tải, giúp kiểm soát vận tốc của phương tiện khi di chuyển trên đường thẳng.
- Trong kỹ thuật, giúp thiết kế các hệ thống cơ học hoạt động ổn định.
- Trong nghiên cứu khoa học, giúp hiểu rõ hơn về các hiện tượng chuyển động trong tự nhiên.
.png)
1. Khái niệm chuyển động thẳng đều
Chuyển động thẳng đều là loại chuyển động trong đó một vật di chuyển theo một đường thẳng với tốc độ không thay đổi. Điều này có nghĩa là vật chuyển động với vận tốc không thay đổi theo thời gian, và không có sự thay đổi về hướng di chuyển.
Đặc điểm chính của chuyển động thẳng đều bao gồm:
- Vận tốc không đổi: Vận tốc của vật không thay đổi theo thời gian.
- Hướng chuyển động không thay đổi: Vật luôn di chuyển theo một đường thẳng.
- Gia tốc bằng 0: Vì vận tốc không thay đổi, nên gia tốc của vật trong chuyển động thẳng đều bằng 0.
Công thức cơ bản liên quan đến chuyển động thẳng đều là:
- Vận tốc (v): Vận tốc là tỉ lệ giữa quãng đường di chuyển và thời gian. Công thức tính vận tốc là: \[ v = \frac{S}{t} \] trong đó \(S\) là quãng đường và \(t\) là thời gian.
- Quãng đường (S): Quãng đường di chuyển được tính bằng sản phẩm của vận tốc và thời gian: \[ S = v \cdot t \]
| Đại lượng | Ký hiệu | Công thức |
|---|---|---|
| Vận tốc | v | \[ v = \frac{S}{t} \] |
| Quãng đường | S | \[ S = v \cdot t \] |
2. Công thức liên quan đến chuyển động thẳng đều
Trong chuyển động thẳng đều, các công thức liên quan chủ yếu đến vận tốc và quãng đường, với đặc điểm nổi bật là vận tốc không thay đổi theo thời gian. Dưới đây là các công thức cơ bản:
- Công thức tính vận tốc:
Vận tốc của một vật trong chuyển động thẳng đều được xác định bằng tỉ lệ giữa quãng đường di chuyển \( S \) và thời gian \( t \). Công thức là:
\[
v = \frac{S}{t}
\] - Công thức tính quãng đường:
Quãng đường mà vật đi được trong chuyển động thẳng đều có thể tính bằng tích của vận tốc và thời gian. Công thức là:
\[
S = v \cdot t
\] - Công thức tính thời gian:
Thời gian di chuyển trong chuyển động thẳng đều có thể được tính bằng tỉ lệ giữa quãng đường và vận tốc:
\[
t = \frac{S}{v}
\]
Dưới đây là bảng tóm tắt các công thức:
| Đại lượng | Công thức | Giải thích |
|---|---|---|
| Vận tốc | \( v = \frac{S}{t} \) | Vận tốc là tỉ lệ giữa quãng đường và thời gian |
| Quãng đường | \( S = v \cdot t \) | Quãng đường bằng vận tốc nhân thời gian |
| Thời gian | \( t = \frac{S}{v} \) | Thời gian bằng quãng đường chia cho vận tốc |

3. Gia tốc trong chuyển động thẳng đều
Trong chuyển động thẳng đều, gia tốc của vật là một yếu tố quan trọng nhưng có một đặc điểm đặc biệt. Để hiểu rõ hơn về gia tốc trong loại chuyển động này, chúng ta cần nắm rõ các khái niệm và tính chất cơ bản.
- Khái niệm gia tốc:
Gia tốc là đại lượng thể hiện sự thay đổi của vận tốc theo thời gian. Được ký hiệu là \(a\), gia tốc được tính bằng tỉ lệ giữa sự thay đổi của vận tốc và thời gian cần thiết để xảy ra sự thay đổi đó:
\[
a = \frac{\Delta v}{\Delta t}
\] - Tại sao gia tốc bằng 0 trong chuyển động thẳng đều:
Trong chuyển động thẳng đều, vận tốc của vật không thay đổi theo thời gian. Vì gia tốc là sự thay đổi của vận tốc theo thời gian, khi vận tốc không thay đổi, điều này dẫn đến gia tốc bằng 0. Công thức thể hiện điều này là:
\[
a = \frac{v - v_0}{t} = \frac{0}{t} = 0
\]
trong đó \(v\) là vận tốc hiện tại, \(v_0\) là vận tốc ban đầu và \(t\) là thời gian.
Với gia tốc bằng 0, chuyển động thẳng đều cho phép chúng ta dễ dàng dự đoán quãng đường và thời gian di chuyển dựa trên các công thức đã biết mà không cần phải tính đến sự thay đổi trong gia tốc.
| Đại lượng | Công thức | Giải thích |
|---|---|---|
| Gia tốc | \( a = \frac{\Delta v}{\Delta t} \) | Gia tốc là sự thay đổi của vận tốc theo thời gian |
| Gia tốc trong chuyển động thẳng đều | \( a = 0 \) | Vận tốc không thay đổi, do đó gia tốc bằng 0 |

XEM THÊM:
4. Ví dụ minh họa và bài tập ứng dụng
Để hiểu rõ hơn về chuyển động thẳng đều và gia tốc bằng 0, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập ứng dụng. Các ví dụ và bài tập dưới đây sẽ giúp bạn củng cố kiến thức và áp dụng vào thực tiễn.
4.1 Ví dụ tính toán
Ví dụ 1: Một ô tô di chuyển trên một đoạn đường thẳng với vận tốc không đổi 60 km/h. Tính quãng đường mà ô tô đi được trong 2 giờ.
- Vận tốc (v) = 60 km/h
- Thời gian (t) = 2 giờ
- Công thức tính quãng đường: \[ S = v \cdot t \]
- Áp dụng công thức: \[ S = 60 \, \text{km/h} \times 2 \, \text{giờ} = 120 \, \text{km} \]
- Vậy, ô tô đi được 120 km trong 2 giờ.
Ví dụ 2: Một người đi bộ với vận tốc ổn định 5 m/s. Tính thời gian cần thiết để đi một quãng đường 300 mét.
- Vận tốc (v) = 5 m/s
- Quãng đường (S) = 300 mét
- Công thức tính thời gian: \[ t = \frac{S}{v} \]
- Áp dụng công thức: \[ t = \frac{300 \, \text{m}}{5 \, \text{m/s}} = 60 \, \text{giây} \]
- Vậy, người đi bộ cần 60 giây để đi 300 mét.
4.2 Bài tập vận dụng
Bài tập 1: Một xe đạp di chuyển theo đường thẳng với vận tốc 12 km/h. Hãy tính quãng đường xe đạp di chuyển được trong 1 giờ 30 phút.
- Vận tốc (v) = 12 km/h
- Thời gian (t) = 1.5 giờ (1 giờ 30 phút)
- Công thức tính quãng đường: \[ S = v \cdot t \]
- Áp dụng công thức: \[ S = 12 \, \text{km/h} \times 1.5 \, \text{giờ} = 18 \, \text{km} \]
- Vậy, xe đạp di chuyển được 18 km trong 1 giờ 30 phút.
Bài tập 2: Một tàu thủy di chuyển trên mặt nước với vận tốc 25 m/s. Tính thời gian để tàu thủy đi hết 5000 mét.
- Vận tốc (v) = 25 m/s
- Quãng đường (S) = 5000 mét
- Công thức tính thời gian: \[ t = \frac{S}{v} \]
- Áp dụng công thức: \[ t = \frac{5000 \, \text{m}}{25 \, \text{m/s}} = 200 \, \text{giây} \]
- Vậy, tàu thủy cần 200 giây để đi hết 5000 mét.

5. Mở rộng: Chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là một dạng chuyển động trong đó gia tốc của vật không đổi theo thời gian. Điều này có nghĩa là vận tốc của vật thay đổi đều đặn, tạo ra một gia tốc cố định.
5.1 Định nghĩa chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là chuyển động của một vật dọc theo một đường thẳng với gia tốc không đổi. Trong loại chuyển động này, tốc độ của vật thay đổi theo một tỷ lệ cố định. Gia tốc (\(a\)) được tính bằng:
\[
a = \frac{\Delta v}{\Delta t}
\]
trong đó \(\Delta v\) là sự thay đổi của vận tốc và \(\Delta t\) là thời gian cần thiết để sự thay đổi này xảy ra.
5.2 Công thức tính gia tốc trong chuyển động thẳng biến đổi đều
Trong chuyển động thẳng biến đổi đều, các công thức cơ bản bao gồm:
- Công thức tính vận tốc: \[ v = v_0 + a \cdot t \] trong đó \(v\) là vận tốc tại thời điểm \(t\), \(v_0\) là vận tốc ban đầu, và \(a\) là gia tốc.
- Công thức tính quãng đường: \[ S = v_0 \cdot t + \frac{1}{2} a \cdot t^2 \] trong đó \(S\) là quãng đường vật di chuyển được, \(t\) là thời gian, và \(a\) là gia tốc.
- Công thức liên quan đến vận tốc và quãng đường: \[ v^2 = v_0^2 + 2 a \cdot S \] trong đó \(v\) là vận tốc cuối cùng, \(v_0\) là vận tốc ban đầu, và \(S\) là quãng đường.
5.3 Ví dụ minh họa
Ví dụ 1: Một xe hơi bắt đầu di chuyển từ trạng thái đứng yên và có gia tốc 2 m/s². Tính vận tốc của xe sau 5 giây và quãng đường xe đã di chuyển.
- Gia tốc (\(a\)) = 2 m/s²
- Thời gian (\(t\)) = 5 giây
- Công thức tính vận tốc: \[ v = v_0 + a \cdot t = 0 + 2 \cdot 5 = 10 \, \text{m/s} \]
- Công thức tính quãng đường: \[ S = v_0 \cdot t + \frac{1}{2} a \cdot t^2 = 0 \cdot 5 + \frac{1}{2} \cdot 2 \cdot 5^2 = 25 \, \text{m} \]
- Vậy, sau 5 giây, vận tốc của xe là 10 m/s và quãng đường xe đã di chuyển là 25 mét.