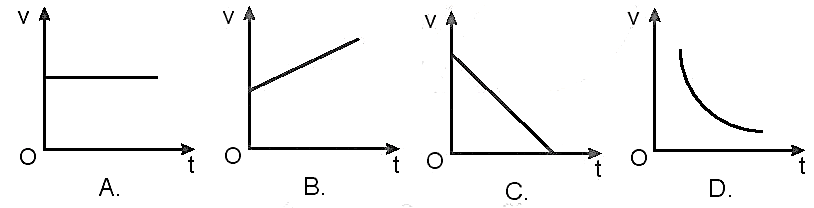
Chủ đề trong chuyển động thẳng đều thì: Trong bài viết này, chúng ta sẽ cùng khám phá các khái niệm cơ bản về chuyển động thẳng đều, từ định nghĩa, công thức tính vận tốc, đến các bài tập minh họa cụ thể. Bài viết nhằm cung cấp cái nhìn tổng quan và chi tiết về chuyển động thẳng đều, giúp bạn hiểu rõ hơn về loại chuyển động cơ bản này.
Mục lục
Chuyển động thẳng đều
Chuyển động thẳng đều là một dạng chuyển động có quỹ đạo là đường thẳng, trong đó vật chuyển động với vận tốc không đổi theo thời gian. Điều này có nghĩa là trong chuyển động thẳng đều, tốc độ và hướng của vật không thay đổi.
Đặc điểm của chuyển động thẳng đều
- Quỹ đạo của chuyển động là một đường thẳng.
- Vận tốc của vật không đổi trong suốt quá trình chuyển động.
- Gia tốc của vật bằng 0, vì vận tốc không thay đổi.
Công thức cơ bản
Vận tốc trong chuyển động thẳng đều được tính bằng công thức:
\[ v = \frac{s}{t} \]
Trong đó:
- \( v \): Vận tốc (m/s)
- \( s \): Quãng đường đi được (m)
- \( t \): Thời gian để đi hết quãng đường (s)
Phương trình chuyển động
Phương trình mô tả chuyển động thẳng đều có dạng:
\[ x = x_0 + v(t - t_0) \]
Trong đó:
- \( x \): Tọa độ của vật tại thời điểm \( t \)
- \( x_0 \): Tọa độ ban đầu của vật
- \( v \): Vận tốc không đổi
- \( t_0 \): Thời gian ban đầu
Để đơn giản, thường chọn \( t_0 = 0 \), khi đó phương trình có thể rút gọn thành:
\[ x = x_0 + v \cdot t \]
Đồ thị tọa độ - thời gian
Trong chuyển động thẳng đều, đồ thị tọa độ - thời gian là một đường thẳng. Phương trình của đồ thị có dạng:
\[ x = x_0 + v \cdot t \]
Độ dốc của đường thẳng trên đồ thị chính là vận tốc \( v \). Nếu vận tốc dương, đồ thị sẽ dốc lên; nếu vận tốc âm, đồ thị sẽ dốc xuống.
Quãng đường và độ dời
- Quãng đường: Là độ dài thực tế mà vật di chuyển.
- Độ dời: Là hiệu giữa tọa độ cuối và tọa độ đầu của vật, không phụ thuộc vào quỹ đạo di chuyển.
Ví dụ thực tế
Giả sử một ô tô chuyển động thẳng đều với vận tốc 60 km/h trong 2 giờ, quãng đường đi được sẽ là:
\[ s = v \cdot t = 60 \cdot 2 = 120 \, \text{km} \]
Tóm tắt
Chuyển động thẳng đều là một trong những dạng chuyển động cơ bản, với vận tốc không thay đổi theo thời gian. Các yếu tố chính gồm quỹ đạo thẳng, vận tốc không đổi và gia tốc bằng 0. Phương trình và đồ thị của chuyển động này đơn giản nhưng mang nhiều ứng dụng trong thực tế.
.png)
1. Khái niệm và định nghĩa về chuyển động thẳng đều
Chuyển động thẳng đều là một loại chuyển động trong đó một vật di chuyển theo một đường thẳng với vận tốc không đổi. Vận tốc không đổi có nghĩa là vật di chuyển với cùng một tốc độ và theo cùng một hướng trong toàn bộ quãng đường di chuyển.
1.1. Định nghĩa
Chuyển động thẳng đều xảy ra khi một vật có quỹ đạo là một đường thẳng và vận tốc của nó không thay đổi theo thời gian. Điều này có nghĩa là sự thay đổi vị trí của vật trong khoảng thời gian nhất định là đồng đều.
1.2. Đặc điểm
- Vận tốc: Là đại lượng không thay đổi, và được tính bằng
v = \frac{s}{t}, trong đóslà quãng đường vàtlà thời gian. - Quỹ đạo: Đường đi của vật là một đường thẳng.
- Gia tốc: Bằng không, vì vận tốc không thay đổi.
1.3. Phương trình chuyển động
Phương trình chuyển động trong chuyển động thẳng đều có dạng:
Trong đó:
slà vị trí của vật tại thời điểmt,vlà vận tốc của vật,s_0là vị trí ban đầu của vật.
2. Công thức tính vận tốc và phương trình chuyển động
Trong chuyển động thẳng đều, vật di chuyển trên một quỹ đạo thẳng với vận tốc không đổi. Điều này có nghĩa là trong mỗi khoảng thời gian như nhau, vật di chuyển được quãng đường bằng nhau. Công thức tính vận tốc và phương trình chuyển động của vật trong chuyển động thẳng đều được biểu diễn như sau:
2.1. Công thức tính vận tốc trong chuyển động thẳng đều
Vận tốc trong chuyển động thẳng đều được xác định bằng thương số giữa quãng đường di chuyển được và thời gian chuyển động:
Trong đó:
- \(v\): Vận tốc (m/s)
- \(s\): Quãng đường di chuyển (m)
- \(t\): Thời gian di chuyển (s)
Vận tốc trong chuyển động thẳng đều không thay đổi về độ lớn và hướng. Do đó, vận tốc trung bình và vận tốc tức thời của vật trong suốt quá trình chuyển động đều là như nhau.
2.2. Phương trình chuyển động của vật chuyển động thẳng đều
Phương trình chuyển động của một vật trong chuyển động thẳng đều được xác định như sau:
Trong đó:
- \(x\): Tọa độ của vật tại thời điểm \(t\) (m)
- \(x_0\): Tọa độ ban đầu của vật tại thời điểm \(t = 0\) (m)
- \(v\): Vận tốc của vật (m/s)
- \(t\): Thời gian chuyển động (s)
Phương trình này cho biết tọa độ của vật thay đổi theo thời gian trong chuyển động thẳng đều. Khi biết vận tốc, tọa độ ban đầu và thời gian, ta có thể tính được vị trí của vật tại bất kỳ thời điểm nào.
2.3. Đồ thị tọa độ - thời gian trong chuyển động thẳng đều
Đồ thị biểu diễn mối quan hệ giữa tọa độ và thời gian trong chuyển động thẳng đều là một đường thẳng. Độ dốc của đường thẳng này chính là vận tốc của vật:
Độ dốc càng lớn thì vận tốc càng cao, nghĩa là vật di chuyển nhanh hơn. Nếu đồ thị là một đường thẳng nằm ngang, điều đó có nghĩa là vật đứng yên (vận tốc bằng 0).

3. Bài tập minh họa về chuyển động thẳng đều
Dưới đây là một số bài tập giúp bạn hiểu rõ hơn về chuyển động thẳng đều, cùng với các bước giải chi tiết.
- Bài tập 1: Tính vận tốc trung bình
- Quãng đường đi được trong 2 giờ đầu: \[ s_1 = v_1 \cdot t_1 = 50 \times 2 = 100 \, km \]
- Quãng đường đi được trong 3 giờ sau: \[ s_2 = v_2 \cdot t_2 = 40 \times 3 = 120 \, km \]
- Tổng quãng đường: \[ s = s_1 + s_2 = 100 + 120 = 220 \, km \]
- Tổng thời gian: \[ t = t_1 + t_2 = 2 + 3 = 5 \, giờ \]
- Vận tốc trung bình của xe: \[ v_{tb} = \frac{s}{t} = \frac{220}{5} = 44 \, km/h \]
- Bài tập 2: Viết phương trình chuyển động
- Phương trình chuyển động thẳng đều: \[ x = x_0 + v \cdot t \]
- Thay các giá trị đã cho vào: \[ x = 5 + 10 \cdot t \]
- Vậy phương trình chuyển động là: \[ x = 5 + 10t \]
- Bài tập 3: Xác định thời điểm gặp nhau của hai vật
- Phương trình chuyển động của vật A: \[ x_A = 0 + 4t \]
- Phương trình chuyển động của vật B: \[ x_B = 10 - 2t \]
- Thời điểm gặp nhau khi \( x_A = x_B \): \[ 4t = 10 - 2t \]
- Giải phương trình: \[ 6t = 10 \Rightarrow t = \frac{10}{6} = \frac{5}{3} \, s \]
- Vị trí gặp nhau: \[ x = 4 \cdot \frac{5}{3} = \frac{20}{3} \, m \]
Giả sử một chiếc xe di chuyển trong 5 giờ. Trong 2 giờ đầu, xe di chuyển với vận tốc 50 km/h, và trong 3 giờ còn lại, vận tốc giảm xuống còn 40 km/h. Hãy tính vận tốc trung bình của xe trong suốt hành trình.
Hướng dẫn giải:
Cho một vật di chuyển thẳng đều với vận tốc 10 m/s, bắt đầu từ vị trí ban đầu \( x_0 = 5 \, m \) và thời gian bắt đầu \( t_0 = 0 \, s \). Viết phương trình chuyển động của vật.
Hướng dẫn giải:
Hai vật A và B bắt đầu chuyển động từ hai điểm khác nhau. Vật A bắt đầu tại vị trí \( x_A = 0 \, m \) và di chuyển với vận tốc \( v_A = 4 \, m/s \), còn vật B bắt đầu tại vị trí \( x_B = 10 \, m \) và di chuyển ngược chiều với vận tốc \( v_B = 2 \, m/s \). Tìm thời điểm và vị trí mà hai vật gặp nhau.
Hướng dẫn giải:
Trên đây là các bài tập minh họa và cách giải chi tiết về chuyển động thẳng đều.

XEM THÊM:
4. Các lưu ý khi học về chuyển động thẳng đều
Khi học về chuyển động thẳng đều, có một số lưu ý quan trọng để nắm bắt kiến thức một cách hiệu quả:
- Định nghĩa cơ bản: Chuyển động thẳng đều là chuyển động của một vật trên một quỹ đạo thẳng với vận tốc không đổi. Điều này có nghĩa là vật đi được quãng đường bằng nhau trong những khoảng thời gian bằng nhau, và gia tốc của vật bằng 0.
- Công thức quan hệ giữa các đại lượng: Công thức chính của chuyển động thẳng đều là:
\[
v = \frac{s}{t}
\]
Trong đó:
- v: Vận tốc của vật (km/h hoặc m/s)
- s: Quãng đường đi được (km hoặc m)
- t: Thời gian chuyển động (giờ hoặc giây)
- Phương trình chuyển động: Phương trình tính vị trí của vật tại một thời điểm t trong chuyển động thẳng đều là:
\[
x = x_0 + v(t - t_0)
\]
Trong đó:
- x: Tọa độ của vật tại thời điểm t
- x_0: Tọa độ ban đầu tại thời điểm t_0
- v: Vận tốc của vật
- Quãng đường và vận tốc: Để tính quãng đường \(s\) mà vật đi được sau khoảng thời gian \(\Delta t\), ta sử dụng công thức: \[ s = v \cdot \Delta t \] Đây là một công thức cơ bản cần ghi nhớ, đặc biệt trong các bài tập liên quan đến tính toán.
- Phân biệt giữa vận tốc và tốc độ: Trong chuyển động thẳng đều, vận tốc là một đại lượng véc tơ, có phương và chiều. Trong khi đó, tốc độ là đại lượng vô hướng, chỉ quan tâm đến độ lớn, không quan tâm phương chiều.
- Thực hành bài tập: Việc làm bài tập minh họa là cực kỳ quan trọng để hiểu rõ hơn mối quan hệ giữa quãng đường, thời gian, và vận tốc. Hãy luyện tập các dạng bài toán tính vận tốc, quãng đường đi được trong thời gian cho trước để củng cố kiến thức.
Với những lưu ý trên, bạn sẽ dễ dàng hơn trong việc nắm bắt và vận dụng kiến thức về chuyển động thẳng đều vào giải quyết các bài toán thực tiễn.