Một Chiếc Thuyền Chuyển Động Thẳng Đều: Khám Phá Định Nghĩa, Công Thức và Ứng Dụng

Một chiếc thuyền chuyển động thẳng đều là một bài toán thường gặp trong vật lý. Khi thuyền chuyển động thẳng đều, vận tốc của nó không thay đổi theo thời gian. Điều này có nghĩa là quãng đường mà thuyền đi được trong một khoảng thời gian nhất định luôn tỉ lệ thuận với thời gian đó.

Các Thông Số Liên Quan Đến Chuyển Động Thẳng Đều

• Vận tốc (v): Là đại lượng chỉ quãng đường đi được trong một đơn vị thời gian, thường tính bằng km/h hoặc m/s.
• Quãng đường (s): Quãng đường mà thuyền đi được trong một khoảng thời gian nhất định.
• Thời gian (t): Thời gian thuyền chuyển động, thường tính bằng giây (s) hoặc giờ (h).

Công thức cơ bản của chuyển động thẳng đều:

Ví Dụ Cụ Thể

Giả sử một chiếc thuyền chuyển động thẳng đều từ điểm A đến điểm B với vận tốc không đổi so với mặt nước là 7 km/h. Nếu quãng đường từ A đến B là 21 km, ta có thể tính được thời gian để thuyền đến nơi bằng cách áp dụng công thức:

Thuyền sẽ mất 3 giờ để di chuyển từ A đến B.

Công Thức Cộng Vận Tốc Trong Chuyển Động Của Thuyền

Khi thuyền chuyển động trên sông, nếu dòng nước chảy theo chiều của thuyền hoặc ngược chiều, vận tốc tổng của thuyền đối với bờ sẽ được tính bằng công thức cộng vận tốc:

• Vận tốc xuôi dòng: Nếu thuyền đi xuôi dòng, vận tốc của thuyền so với bờ sẽ là tổng vận tốc của thuyền và vận tốc của dòng nước.
• Vận tốc ngược dòng: Nếu thuyền đi ngược dòng, vận tốc của thuyền so với bờ sẽ là hiệu vận tốc của thuyền và vận tốc của dòng nước.

Ví dụ, nếu vận tốc của thuyền là 12 km/h và vận tốc dòng nước là 2 km/h, khi đi xuôi dòng, vận tốc tổng của thuyền sẽ là:

Và khi đi ngược dòng:

Kết Luận

Chuyển động thẳng đều của thuyền là một bài toán cơ bản nhưng rất hữu ích để hiểu rõ hơn về khái niệm vận tốc, quãng đường và thời gian trong cơ học. Công thức cộng vận tốc cũng giúp chúng ta mô tả chính xác hơn khi có sự tham gia của dòng nước.

Chuyển động thẳng đều là một loại chuyển động trong đó một vật di chuyển trên một đường thẳng với vận tốc không thay đổi theo thời gian. Đây là khái niệm cơ bản trong vật lý, giúp chúng ta hiểu về mối liên hệ giữa vận tốc, quãng đường và thời gian.

1.1. Định Nghĩa

Chuyển động thẳng đều được định nghĩa là chuyển động của một vật trên một quỹ đạo thẳng, trong đó vận tốc của vật không thay đổi. Điều này có nghĩa là gia tốc của vật bằng không.

1.2. Đặc Điểm

• Vận tốc không đổi: Vận tốc của vật trong chuyển động thẳng đều luôn giữ nguyên giá trị.
• Gia tốc bằng không: Do vận tốc không thay đổi, gia tốc của vật trong chuyển động thẳng đều là bằng không.
• Quỹ đạo thẳng: Đường đi của vật là một đường thẳng, không có sự cong vênh.

1.3. Công Thức Liên Hệ

Để tính toán các yếu tố trong chuyển động thẳng đều, ta có thể sử dụng công thức cơ bản sau:

Trong đó:

• v: Vận tốc của vật (m/s hoặc km/h).
• s: Quãng đường vật đã đi được (m hoặc km).
• t: Thời gian vật đã di chuyển (s hoặc h).

1.4. Phương Trình Chuyển Động

Phương trình chuyển động thẳng đều có dạng:

Trong đó:

• x: Tọa độ của vật tại thời điểm t.
• x_0: Tọa độ của vật tại thời điểm ban đầu (t=0).
• v: Vận tốc của vật.
• t: Thời gian kể từ thời điểm ban đầu.

1.5. Ví Dụ Minh Họa

Giả sử một chiếc thuyền chuyển động thẳng đều với vận tốc 5 km/h. Nếu thời gian thuyền di chuyển là 2 giờ, quãng đường mà thuyền đã đi được có thể tính bằng công thức:

Do đó, thuyền đã đi được quãng đường 10 km trong 2 giờ.

Trong chuyển động thẳng đều, phương trình chuyển động giúp chúng ta xác định vị trí của vật tại bất kỳ thời điểm nào trong quá trình di chuyển. Phương trình này biểu diễn mối quan hệ giữa vị trí, vận tốc và thời gian trong chuyển động thẳng đều.

2.1. Phương Trình Tổng Quát

Phương trình tổng quát của chuyển động thẳng đều có dạng:

Trong đó:

• x: Vị trí của vật tại thời điểm \( t \) (m hoặc km).
• x_0: Vị trí ban đầu của vật (m hoặc km).
• v: Vận tốc của vật (m/s hoặc km/h).
• t: Thời gian di chuyển (s hoặc h).

2.2. Ý Nghĩa Của Phương Trình

• Vị trí \( x \) của vật tại thời điểm \( t \) phụ thuộc vào vị trí ban đầu \( x_0 \) và vận tốc \( v \).
• Nếu biết vận tốc và thời gian di chuyển, ta có thể tính được quãng đường mà vật đã đi được.

2.3. Ví Dụ Minh Họa

Giả sử một chiếc thuyền bắt đầu từ vị trí \( x_0 = 0 \) và di chuyển với vận tốc không đổi \( v = 6 \, \text{km/h} \). Sau 3 giờ, vị trí của thuyền có thể được tính bằng phương trình:

Như vậy, sau 3 giờ, thuyền đã di chuyển được 18 km.

Để hiểu rõ hơn về chuyển động thẳng đều, chúng ta hãy cùng phân tích một số ví dụ minh họa. Dưới đây là các tình huống cụ thể về chuyển động của một chiếc thuyền trên sông với vận tốc không đổi.

3.1. Ví Dụ 1: Thuyền Di Chuyển Xuôi Dòng

Giả sử một chiếc thuyền di chuyển xuôi dòng với vận tốc không đổi so với dòng nước là \( v_{\text{thuyền}} = 10 \, \text{km/h} \). Dòng nước chảy với vận tốc \( v_{\text{nước}} = 2 \, \text{km/h} \). Vận tốc của thuyền so với bờ sẽ được tính bằng cách cộng vận tốc của thuyền và vận tốc của dòng nước:

Như vậy, vận tốc của thuyền so với bờ là 12 km/h. Nếu thuyền di chuyển trong 3 giờ, quãng đường đi được là:

Thuyền sẽ đi được 36 km trong 3 giờ.

3.2. Ví Dụ 2: Thuyền Di Chuyển Ngược Dòng

Nếu thuyền di chuyển ngược dòng, vận tốc của nó so với bờ sẽ là hiệu của vận tốc thuyền và vận tốc dòng nước. Giả sử vận tốc của thuyền so với nước vẫn là \( v_{\text{thuyền}} = 10 \, \text{km/h} \) và vận tốc của dòng nước là \( v_{\text{nước}} = 2 \, \text{km/h} \). Vận tốc của thuyền so với bờ sẽ là:

Trong trường hợp này, nếu thuyền di chuyển trong 2 giờ, quãng đường đi được sẽ là:

Thuyền sẽ đi được 16 km trong 2 giờ.

3.3. Ví Dụ 3: Thuyền Di Chuyển Trong Nước Yên Tĩnh

Trong trường hợp thuyền di chuyển trong nước yên tĩnh, tức là không có dòng chảy, vận tốc của thuyền so với bờ sẽ bằng vận tốc của thuyền so với nước. Nếu vận tốc thuyền là \( v_{\text{thuyền}} = 5 \, \text{km/h} \) và thuyền di chuyển trong 4 giờ, quãng đường thuyền đi được sẽ là:

Trong 4 giờ, thuyền đã đi được 20 km trong nước yên tĩnh.

Đồ thị chuyển động thẳng đều là một công cụ trực quan để mô tả mối quan hệ giữa các đại lượng như vận tốc, quãng đường và thời gian. Dưới đây là các dạng đồ thị phổ biến trong chuyển động thẳng đều.

4.1. Đồ Thị Quãng Đường - Thời Gian (x - t)

Trong chuyển động thẳng đều, đồ thị biểu diễn mối quan hệ giữa quãng đường \( x \) và thời gian \( t \) là một đường thẳng có độ dốc không đổi. Độ dốc của đường thẳng này tương ứng với vận tốc của vật.

Phương trình của đồ thị quãng đường - thời gian là:

Trong đó:

• \( x_0 \): Vị trí ban đầu của vật.
• \( v \): Vận tốc không đổi của vật.
• \( t \): Thời gian di chuyển.

Nếu vật bắt đầu từ vị trí \( x_0 = 0 \), phương trình trở thành:

Đồ thị này là một đường thẳng xuất phát từ gốc tọa độ (0,0) nếu vật bắt đầu di chuyển từ vị trí ban đầu.

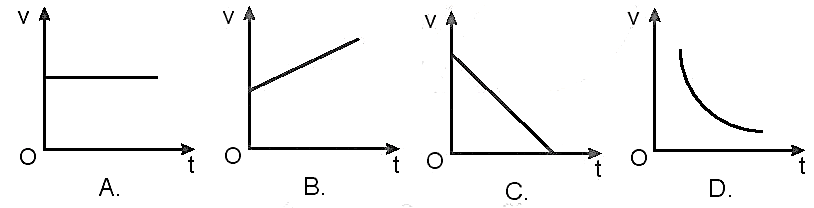
4.2. Đồ Thị Vận Tốc - Thời Gian (v - t)

Trong chuyển động thẳng đều, vận tốc của vật không thay đổi theo thời gian. Do đó, đồ thị vận tốc - thời gian là một đường thẳng song song với trục thời gian, với giá trị vận tốc không đổi.

Đồ thị có dạng:

Điều này có nghĩa là tại mọi thời điểm, vận tốc của vật đều giữ nguyên, thể hiện tính chất của chuyển động thẳng đều.

4.3. Đồ Thị Gia Tốc - Thời Gian (a - t)

Gia tốc trong chuyển động thẳng đều bằng 0, do vận tốc không thay đổi. Vì vậy, đồ thị gia tốc - thời gian là một đường nằm ngang trên trục \( t \) tại giá trị \( a = 0 \).

Phương trình của đồ thị là:

Điều này cho thấy vật không có sự thay đổi về vận tốc, hay nói cách khác, không có gia tốc trong chuyển động thẳng đều.

Để củng cố kiến thức về chuyển động thẳng đều, hãy cùng giải một số bài tập thực hành dưới đây. Các bài tập này sẽ giúp bạn hiểu rõ hơn về cách áp dụng các công thức và phương trình vào thực tế.

5.1. Bài Tập 1

Một chiếc thuyền di chuyển với vận tốc không đổi là \( 12 \, \text{km/h} \). Hãy tính quãng đường mà thuyền đã đi được sau 3 giờ.

• Giải:
• Vận tốc của thuyền: \( v = 12 \, \text{km/h} \)
• Thời gian di chuyển: \( t = 3 \, \text{giờ} \)
• Quãng đường di chuyển: \[ s = v \times t = 12 \times 3 = 36 \, \text{km} \]

Vậy, thuyền đã di chuyển được quãng đường 36 km sau 3 giờ.

5.2. Bài Tập 2

Một chiếc thuyền xuất phát từ vị trí ban đầu \( x_0 = 0 \) và di chuyển thẳng đều với vận tốc \( v = 15 \, \text{km/h} \). Hãy viết phương trình chuyển động của thuyền và tính vị trí của thuyền sau 4 giờ.

• Giải:
• Vị trí ban đầu: \( x_0 = 0 \)
• Vận tốc của thuyền: \( v = 15 \, \text{km/h} \)
• Thời gian di chuyển: \( t = 4 \, \text{giờ} \)
• Phương trình chuyển động: \[ x = x_0 + v \times t = 0 + 15 \times t = 15 t \]
• Vị trí sau 4 giờ: \[ x = 15 \times 4 = 60 \, \text{km} \]

Vậy, sau 4 giờ, thuyền sẽ ở vị trí cách điểm xuất phát 60 km.

5.3. Bài Tập 3

Một chiếc thuyền di chuyển từ vị trí \( x_0 = 5 \, \text{km} \) với vận tốc \( 10 \, \text{km/h} \). Hãy tính thời gian cần thiết để thuyền đi được quãng đường 25 km.

• Giải:
• Vị trí ban đầu: \( x_0 = 5 \, \text{km} \)
• Vận tốc: \( v = 10 \, \text{km/h} \)
• Quãng đường cần đi: \( s = 25 \, \text{km} \)
• Thời gian cần thiết: \[ t = \frac{s}{v} = \frac{25}{10} = 2,5 \, \text{giờ} \]

Vậy, thuyền cần 2,5 giờ để di chuyển quãng đường 25 km.

Chuyển động thẳng đều có rất nhiều ứng dụng trong thực tiễn, đặc biệt trong các lĩnh vực như giao thông, kỹ thuật, và công nghiệp. Những ví dụ sau đây minh họa ứng dụng của chuyển động thẳng đều trong đời sống hàng ngày:

6.1. Trong Thực Tiễn

Chuyển động thẳng đều được sử dụng để mô phỏng các tình huống trong giao thông và công nghiệp:

• Trong giao thông đường bộ: Việc tính toán vận tốc đều của các phương tiện như xe máy, ô tô trên đường thẳng giúp tối ưu hóa khoảng cách và thời gian di chuyển.
• Trong sản xuất công nghiệp: Các dây chuyền sản xuất vận hành với tốc độ đều đặn, giúp kiểm soát thời gian và quy trình sản xuất chính xác.

6.2. Trong Giao Thông Đường Thủy

Chuyển động thẳng đều của thuyền trong giao thông đường thủy giúp giải quyết các bài toán về vận tốc và quãng đường trong các điều kiện khác nhau, chẳng hạn như:

1. Khi thuyền di chuyển ngược dòng nước, ta cần tính toán vận tốc của thuyền so với mặt nước và so với dòng chảy để xác định thời gian di chuyển thực tế.
2. Khi thuyền di chuyển xuôi dòng nước, việc tính toán vận tốc kết hợp với vận tốc dòng nước giúp thuyền đạt đến vị trí mong muốn một cách nhanh chóng và hiệu quả.
3. Trong thực tiễn, các bài toán về giao thông đường thủy thường sử dụng phương trình chuyển động thẳng đều để tính toán và tối ưu hóa lịch trình di chuyển, đặc biệt khi xét đến các yếu tố như vận tốc dòng nước, vận tốc của thuyền và điều kiện thời tiết.

Như vậy, chuyển động thẳng đều có vai trò quan trọng trong việc tính toán và dự đoán thời gian di chuyển trong các môi trường có dòng chảy ổn định, hỗ trợ đắc lực cho việc quản lý giao thông và logistics trên các tuyến đường thủy.