Chủ đề bài 7 gia tốc chuyển động thẳng biến đổi đều: Chào mừng bạn đến với bài viết chi tiết về "Bài 7 Gia Tốc Chuyển Động Thẳng Biến Đổi Đều". Bài viết này sẽ cung cấp cái nhìn sâu sắc về gia tốc và chuyển động thẳng biến đổi đều, bao gồm các công thức quan trọng, phân tích đồ thị, và ứng dụng thực tiễn. Hãy cùng khám phá để nắm vững kiến thức vật lý cơ bản và cải thiện kỹ năng giải bài tập của bạn.
Mục lục
Gia tốc – Chuyển động thẳng biến đổi đều
Trong bài học này, chúng ta sẽ tìm hiểu về khái niệm gia tốc trong chuyển động thẳng biến đổi đều. Đây là một kiến thức cơ bản trong vật lý lớp 10, giúp học sinh hiểu rõ hơn về sự thay đổi vận tốc theo thời gian trong chuyển động thẳng.
1. Khái niệm về gia tốc
Gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi của vận tốc trong quá trình chuyển động. Biểu thức tính gia tốc trung bình được biểu diễn như sau:
\[ a = \frac{\Delta v}{\Delta t} \]
Trong đó:
- \( a \) là gia tốc (m/s²)
- \( \Delta v \) là sự thay đổi vận tốc (m/s)
- \( \Delta t \) là khoảng thời gian (s)
2. Chuyển động thẳng nhanh dần đều
Chuyển động thẳng nhanh dần đều là chuyển động trong đó vận tốc của vật tăng đều theo thời gian, và gia tốc là hằng số. Biểu thức tính vận tốc tức thời trong chuyển động nhanh dần đều là:
\[ v = v_0 + a t \]
Trong đó:
- \( v_0 \) là vận tốc ban đầu (m/s)
- \( t \) là thời gian (s)
3. Chuyển động thẳng chậm dần đều
Chuyển động thẳng chậm dần đều là khi vận tốc của vật giảm đều theo thời gian. Gia tốc trong trường hợp này có giá trị âm, tức là ngược chiều với vận tốc. Công thức tính vận tốc trong chuyển động chậm dần đều cũng tương tự như với chuyển động nhanh dần đều:
\[ v = v_0 - a t \]
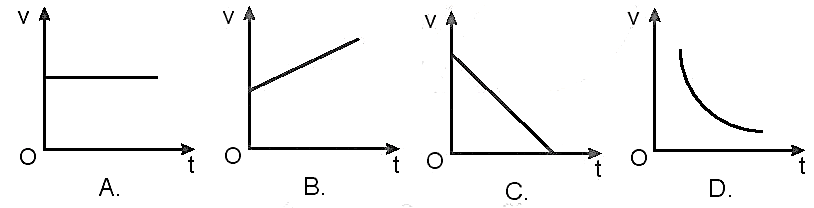
4. Đồ thị vận tốc - thời gian
Đồ thị vận tốc - thời gian trong chuyển động thẳng biến đổi đều là một đường thẳng. Đối với chuyển động nhanh dần đều, đường thẳng có độ dốc dương, còn đối với chuyển động chậm dần đều, đường thẳng có độ dốc âm.
5. Bài tập mẫu
Ví dụ: Một chiếc xe bắt đầu chuyển động với vận tốc ban đầu là 5 m/s và gia tốc không đổi là 2 m/s². Hãy tính vận tốc của xe sau 10 giây.
Giải:
Sử dụng công thức \[ v = v_0 + a t \], ta có:
\[ v = 5 + 2 \times 10 = 25 \, m/s \]
6. Kết luận
Gia tốc và chuyển động thẳng biến đổi đều là các khái niệm nền tảng trong vật lý, giúp mô tả chi tiết hơn về sự thay đổi vận tốc của vật trong chuyển động. Việc nắm vững các kiến thức này sẽ giúp học sinh hiểu rõ hơn về các hiện tượng trong đời sống hàng ngày.

.png)
1. Tổng Quan về Gia Tốc và Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều là dạng chuyển động có gia tốc không đổi. Điều này có nghĩa là trong suốt quá trình chuyển động, vận tốc của vật thay đổi đều đặn theo thời gian, tạo ra một mối quan hệ rõ ràng giữa gia tốc, vận tốc, và quãng đường đi được. Để hiểu rõ hơn, ta cần tìm hiểu về khái niệm gia tốc cũng như cách tính toán và áp dụng trong chuyển động thẳng biến đổi đều.
1.1. Khái Niệm Gia Tốc
Gia tốc \(a\) là đại lượng biểu thị sự thay đổi vận tốc của vật theo thời gian. Trong chuyển động thẳng biến đổi đều, gia tốc được tính bằng tỉ lệ giữa sự thay đổi vận tốc và khoảng thời gian diễn ra sự thay đổi đó. Công thức tính gia tốc là:
\[ a = \frac{\Delta v}{\Delta t} \]
Trong đó:
- \(\Delta v\) là sự thay đổi vận tốc (\(v_2 - v_1\))
- \(\Delta t\) là khoảng thời gian diễn ra sự thay đổi vận tốc
1.2. Chuyển Động Thẳng Biến Đổi Đều
Trong chuyển động thẳng biến đổi đều, gia tốc không thay đổi và có hai trường hợp:
- Chuyển động nhanh dần đều: Vận tốc của vật tăng dần theo thời gian, tức là gia tốc dương (\(a > 0\)).
- Chuyển động chậm dần đều: Vận tốc của vật giảm dần theo thời gian, tức là gia tốc âm (\(a < 0\)).
1.3. Công Thức Cơ Bản Của Chuyển Động Thẳng Biến Đổi Đều
Các công thức cơ bản thường dùng để mô tả chuyển động thẳng biến đổi đều bao gồm:
- Phương trình vận tốc:
- Phương trình quãng đường:
- Phương trình liên hệ giữa vận tốc và quãng đường:
\[ v = v_0 + a t \]
\[ s = v_0 t + \frac{1}{2} a t^2 \]
\[ v^2 = v_0^2 + 2 a s \]
1.4. Ý Nghĩa của Gia Tốc Trong Thực Tế
Trong đời sống hàng ngày, gia tốc có thể thấy rõ trong nhiều tình huống, chẳng hạn như khi xe ô tô tăng tốc trên đường hoặc khi tàu hoả giảm tốc để dừng lại. Hiểu về gia tốc và các công thức liên quan đến chuyển động thẳng biến đổi đều giúp chúng ta áp dụng vào việc tính toán và dự đoán chuyển động của các vật thể trong thực tế một cách chính xác.
Chuyển động thẳng biến đổi đều là một khái niệm cơ bản nhưng quan trọng trong vật lý, giúp chúng ta hiểu rõ hơn về cách các vật thể di chuyển trong không gian và thời gian.
2. Các Công Thức Quan Trọng
Trong chuyển động thẳng biến đổi đều, việc áp dụng các công thức chính xác là rất quan trọng để giải quyết các bài toán vật lý. Dưới đây là các công thức cơ bản và quan trọng giúp mô tả và phân tích chuyển động thẳng biến đổi đều.
2.1. Công Thức Tính Gia Tốc
Gia tốc (\(a\)) là đại lượng mô tả sự thay đổi của vận tốc theo thời gian. Công thức tính gia tốc là:
\[ a = \frac{\Delta v}{\Delta t} \]
Trong đó:
- \(\Delta v\) là sự thay đổi vận tốc (\(v - v_0\))
- \(\Delta t\) là khoảng thời gian (\(t\))
2.2. Công Thức Tính Vận Tốc
Vận tốc tức thời (\(v\)) tại một thời điểm cụ thể có thể được tính bằng công thức:
\[ v = v_0 + a t \]
Trong đó:
- \(v_0\) là vận tốc ban đầu
- \(a\) là gia tốc
- \(t\) là thời gian
2.3. Công Thức Tính Quãng Đường
Quãng đường (\(s\)) đi được trong một khoảng thời gian có thể tính bằng công thức:
\[ s = v_0 t + \frac{1}{2} a t^2 \]
Trong đó:
- \(v_0\) là vận tốc ban đầu
- \(a\) là gia tốc
- \(t\) là thời gian
2.4. Công Thức Liên Hệ Giữa Vận Tốc và Quãng Đường
Khi biết vận tốc và gia tốc, ta có thể tính được quãng đường bằng công thức:
\[ v^2 = v_0^2 + 2 a s \]
Trong đó:
- \(v\) là vận tốc cuối cùng
- \(v_0\) là vận tốc ban đầu
- \(a\) là gia tốc
- \(s\) là quãng đường
2.5. Bảng Tóm Tắt Các Công Thức
| Công Thức | Mô Tả |
|---|---|
| \[ a = \frac{\Delta v}{\Delta t} \] | Tính gia tốc |
| \[ v = v_0 + a t \] | Tính vận tốc |
| \[ s = v_0 t + \frac{1}{2} a t^2 \] | Tính quãng đường |
| \[ v^2 = v_0^2 + 2 a s \] | Tính quãng đường khi biết vận tốc |
Hiểu và áp dụng đúng các công thức trên sẽ giúp bạn giải quyết hiệu quả các bài toán về chuyển động thẳng biến đổi đều và nắm vững kiến thức vật lý cơ bản.

3. Đồ Thị và Phân Tích
Đồ thị là công cụ quan trọng trong việc phân tích chuyển động thẳng biến đổi đều. Bằng cách vẽ và phân tích các đồ thị của vận tốc, gia tốc và quãng đường theo thời gian, chúng ta có thể hiểu rõ hơn về sự thay đổi và mối liên hệ giữa các đại lượng vật lý trong chuyển động này.
3.1. Đồ Thị Vận Tốc - Thời Gian
Đồ thị vận tốc theo thời gian thể hiện sự thay đổi vận tốc của vật trong quá trình chuyển động. Đối với chuyển động thẳng biến đổi đều, đồ thị này là một đường thẳng có độ dốc bằng gia tốc.
Đường thẳng trong đồ thị có dạng:
\[ v = v_0 + a t \]
Trong đó:
- \(v\) là vận tốc tại thời điểm \(t\)
- \(v_0\) là vận tốc ban đầu
- \(a\) là gia tốc
- \(t\) là thời gian
3.2. Đồ Thị Gia Tốc - Thời Gian
Đối với chuyển động thẳng biến đổi đều, gia tốc là hằng số, do đó đồ thị gia tốc theo thời gian là một đường ngang song song với trục hoành.
Đồ thị có dạng:
\[ a = \text{hằng số} \]
3.3. Đồ Thị Quãng Đường - Thời Gian
Đồ thị quãng đường theo thời gian thể hiện sự tăng trưởng quãng đường đi được theo thời gian. Đối với chuyển động thẳng biến đổi đều, đồ thị này có dạng một parabola.
Đồ thị có dạng:
\[ s = v_0 t + \frac{1}{2} a t^2 \]
3.4. Phân Tích Đồ Thị
Khi phân tích các đồ thị trên, chúng ta có thể rút ra các thông tin quan trọng:
- Đồ thị vận tốc - thời gian: Độ dốc của đường thẳng là gia tốc. Một độ dốc dương cho thấy chuyển động nhanh dần đều, trong khi độ dốc âm cho thấy chuyển động chậm dần đều.
- Đồ thị gia tốc - thời gian: Đường thẳng nằm ngang cho biết gia tốc không thay đổi, thể hiện tính chất của chuyển động thẳng biến đổi đều.
- Đồ thị quãng đường - thời gian: Đồ thị hình parabol cho thấy quãng đường tăng theo bình phương thời gian, phản ánh sự gia tăng đều đặn trong quãng đường đi được.
Việc nắm vững và phân tích các đồ thị giúp hiểu rõ hơn về cơ chế chuyển động và các yếu tố ảnh hưởng đến chuyển động thẳng biến đổi đều. Đây là bước quan trọng trong việc giải các bài toán vật lý liên quan đến chuyển động.
4. Các Loại Chuyển Động Thẳng Biến Đổi Đều
4.1 Chuyển Động Nhanh Dần Đều
Chuyển động nhanh dần đều là loại chuyển động thẳng trong đó vận tốc của vật tăng dần theo thời gian. Gia tốc trong chuyển động này là một đại lượng dương và không thay đổi theo thời gian. Công thức cơ bản của chuyển động nhanh dần đều:
- Vận tốc tại thời điểm \(t\): \[ v = v_0 + a t \]
- Quãng đường đi được sau thời gian \(t\): \[ s = v_0 t + \frac{1}{2} a t^2 \]
- Gia tốc \(a\) là một hằng số: \[ a = \frac{\Delta v}{\Delta t} \]
Trong đó:
- \(v_0\): Vận tốc ban đầu.
- \(v\): Vận tốc tại thời điểm \(t\).
- \(a\): Gia tốc.
- \(s\): Quãng đường vật đi được sau thời gian \(t\).
4.2 Chuyển Động Chậm Dần Đều
Chuyển động chậm dần đều là loại chuyển động thẳng trong đó vận tốc của vật giảm dần theo thời gian. Gia tốc trong chuyển động này là một đại lượng âm và không thay đổi theo thời gian. Công thức tương tự như chuyển động nhanh dần đều, nhưng gia tốc có giá trị âm:
- Vận tốc tại thời điểm \(t\): \[ v = v_0 - a t \]
- Quãng đường đi được sau thời gian \(t\): \[ s = v_0 t - \frac{1}{2} a t^2 \]
- Gia tốc \(a\) là một hằng số: \[ a = \frac{\Delta v}{\Delta t} \]
Trong chuyển động chậm dần đều, vật có xu hướng dừng lại sau một thời gian nhất định, khi vận tốc trở về 0.

5. Ứng Dụng Thực Tiễn và Bài Tập
Gia tốc và chuyển động thẳng biến đổi đều không chỉ là những khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tiễn trong cuộc sống. Những ứng dụng này giúp chúng ta hiểu rõ hơn về các hiện tượng vật lý xảy ra hàng ngày, từ đó phát triển các công nghệ và phương pháp tối ưu hóa hoạt động của máy móc và phương tiện giao thông.
5.1. Ứng dụng trong giao thông
- Trong các phương tiện giao thông như ô tô, tàu hỏa và máy bay, gia tốc là yếu tố quan trọng để đo lường sự thay đổi vận tốc theo thời gian. Chẳng hạn, khi xe tăng tốc hoặc giảm tốc, gia tốc sẽ xác định quá trình này diễn ra nhanh hay chậm.
- \[a = \frac{\Delta v}{\Delta t}\]: Công thức tính gia tốc cho thấy mối liên hệ giữa vận tốc và thời gian, giúp tối ưu hóa hiệu suất nhiên liệu và tăng cường an toàn giao thông.
5.2. Ứng dụng trong kỹ thuật và công nghệ
- Gia tốc được sử dụng để kiểm tra độ bền của vật liệu trong kỹ thuật xây dựng và cơ khí. Ví dụ, gia tốc trong các thử nghiệm va đập có thể giúp xác định khả năng chịu lực của vật liệu.
- Trong công nghệ sản xuất, việc tính toán và kiểm soát gia tốc của các bộ phận máy móc giúp nâng cao hiệu suất làm việc và tuổi thọ của thiết bị.
5.3. Bài tập thực hành
Dưới đây là một số bài tập liên quan đến chuyển động thẳng biến đổi đều và gia tốc:
- Một ô tô đang chuyển động với vận tốc ban đầu là 20 m/s, sau đó tăng tốc đều với gia tốc 2 m/s². Tính quãng đường mà ô tô đã đi được sau 5 giây.
- Một vật rơi tự do từ độ cao 100 m. Tính thời gian để vật chạm đất, biết rằng gia tốc trọng trường là \[g = 9.8 m/s^2\].
- Một tàu hỏa bắt đầu khởi hành từ trạng thái đứng yên và đạt vận tốc 72 km/h sau 10 giây. Tính gia tốc của tàu.
Những bài tập trên sẽ giúp củng cố kiến thức về gia tốc và chuyển động thẳng biến đổi đều, đồng thời áp dụng vào các tình huống thực tiễn trong cuộc sống hàng ngày.
XEM THÊM:
6. Tài Liệu Tham Khảo và Nguồn Tài Nguyên
Để hiểu sâu hơn về chủ đề gia tốc và chuyển động thẳng biến đổi đều, dưới đây là các tài liệu tham khảo và nguồn tài nguyên hỗ trợ học tập:
6.1 Sách và Tài Liệu Giáo Khoa
- Sách giáo khoa Vật lý lớp 10 - Bộ Chân trời sáng tạo: Đây là tài liệu chính thức được sử dụng trong hệ thống giáo dục tại Việt Nam. Nội dung bài 7 giúp học sinh nắm rõ định nghĩa gia tốc, phân loại chuyển động thẳng, và các công thức tính toán liên quan. Bài giảng này còn cung cấp các ví dụ và bài tập giúp củng cố kiến thức.
- Sách bài tập Vật lý lớp 10 - Chân trời sáng tạo: Cung cấp thêm các bài tập trắc nghiệm và tự luận từ cơ bản đến nâng cao, hỗ trợ học sinh trong quá trình ôn tập và luyện tập giải đề.
- Sách giáo viên Vật lý 10: Hướng dẫn phương pháp giảng dạy và đưa ra lời giải chi tiết cho các bài tập trong sách giáo khoa, giúp giáo viên dễ dàng truyền đạt kiến thức tới học sinh.
6.2 Tài Nguyên Trực Tuyến và Công Cụ Học Tập
- VnDoc - Lý thuyết Vật lý 10 Bài 7: Trang web này cung cấp tóm tắt lý thuyết và hệ thống bài tập chi tiết về gia tốc và chuyển động thẳng biến đổi đều, kèm theo các phương pháp giải bài tập dễ hiểu.
- VietJack - Giải bài tập Vật lý 10: Cung cấp lời giải chi tiết các câu hỏi trắc nghiệm và tự luận trong sách bài tập Vật lý 10. Đây là nguồn tài liệu giúp học sinh tự kiểm tra và đánh giá quá trình học tập.
- Tech12h - Giải bài 7 Gia tốc - Chuyển động thẳng biến đổi đều: Trang này cung cấp hướng dẫn giải các bài tập từ cơ bản đến nâng cao, phù hợp cho các em học sinh muốn ôn luyện kỹ năng giải đề thi.
- MathJax: Công cụ hỗ trợ soạn thảo và hiển thị các công thức toán học phức tạp trên các trang web, giúp việc học tập các công thức vật lý trở nên dễ dàng hơn.