Chủ đề chuyển động thẳng nhanh dần đều là gì: Chuyển động thẳng nhanh dần đều là một khái niệm quan trọng trong vật lý học, đặc trưng bởi sự gia tăng đều đặn của vận tốc theo thời gian. Bài viết này sẽ giúp bạn hiểu rõ về định nghĩa, công thức tính toán và ứng dụng thực tiễn của chuyển động thẳng nhanh dần đều, từ đó cung cấp cái nhìn toàn diện và chi tiết về chủ đề này.
Mục lục
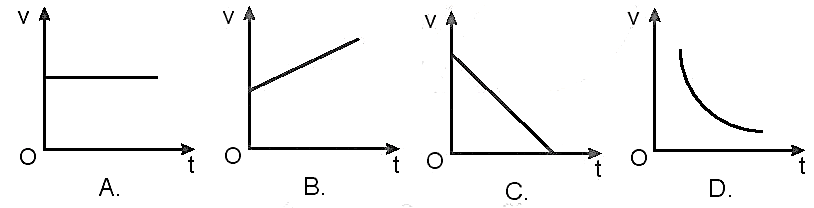
Chuyển Động Thẳng Nhanh Dần Đều Là Gì?
Chuyển động thẳng nhanh dần đều là một dạng chuyển động mà trong đó vận tốc của vật tăng đều theo thời gian, nghĩa là gia tốc của vật không đổi. Loại chuyển động này thường được đặc trưng bởi hai đại lượng cơ bản: vận tốc và gia tốc.
1. Gia tốc trong chuyển động thẳng nhanh dần đều
Gia tốc (\(a\)) là đại lượng đặc trưng cho sự thay đổi của vận tốc (\(v\)) theo thời gian (\(t\)). Gia tốc trong chuyển động thẳng nhanh dần đều luôn dương và không thay đổi.
- Gia tốc: \(a = \dfrac{\Delta v}{\Delta t}\)
- Trong đó:
- \(\Delta v\): Độ biến thiên vận tốc.
- \(\Delta t\): Khoảng thời gian.
- Đơn vị của gia tốc là \(m/s^2\).
2. Công thức tính vận tốc
Vận tốc của vật trong chuyển động thẳng nhanh dần đều được tính theo công thức:
- \(v_0\): Vận tốc ban đầu của vật.
- \(a\): Gia tốc của vật.
- \(t\): Thời gian chuyển động.
3. Công thức tính quãng đường
Quãng đường (\(s\)) mà vật di chuyển trong chuyển động thẳng nhanh dần đều có thể được tính bằng:
- \(v_0\): Vận tốc ban đầu.
- \(a\): Gia tốc.
- \(t\): Thời gian.
4. Đặc điểm của chuyển động thẳng nhanh dần đều
- Vận tốc tăng đều theo thời gian.
- Gia tốc không đổi trong suốt quá trình chuyển động.
- Quãng đường di chuyển tỉ lệ thuận với bình phương thời gian.
5. Ví dụ về chuyển động thẳng nhanh dần đều
- Một chiếc ô tô khởi hành từ trạng thái nghỉ với gia tốc \(a = 2 m/s^2\). Sau 5 giây, vận tốc của ô tô là: \[ v = 0 + 2 \times 5 = 10 \, m/s \]
- Quãng đường ô tô đi được trong thời gian 5 giây: \[ s = 0 \times 5 + \dfrac{1}{2} \times 2 \times 5^2 = 25 \, m \]

.png)
1. Định nghĩa chuyển động thẳng nhanh dần đều
Chuyển động thẳng nhanh dần đều là loại chuyển động trong đó vật di chuyển trên một đường thẳng và vận tốc của vật tăng đều theo thời gian. Điều này có nghĩa là gia tốc của vật luôn không đổi và dương.
Công thức tính vận tốc trong chuyển động thẳng nhanh dần đều được biểu diễn như sau:
- \( v = v_0 + a \cdot t \)
Trong đó:
- \( v \) là vận tốc của vật tại thời điểm \( t \)
- \( v_0 \) là vận tốc ban đầu
- \( a \) là gia tốc không đổi
- \( t \) là thời gian vật di chuyển
Quãng đường đi được trong chuyển động thẳng nhanh dần đều được tính bằng công thức:
- \( s = v_0 \cdot t + \frac{1}{2}a \cdot t^2 \)
Đặc điểm chính của chuyển động thẳng nhanh dần đều là gia tốc luôn có giá trị dương, làm cho vận tốc của vật tăng lên liên tục theo thời gian.
2. Công thức trong chuyển động thẳng nhanh dần đều
Trong chuyển động thẳng nhanh dần đều, có ba công thức chính giúp tính toán các đại lượng liên quan như vận tốc, quãng đường và gia tốc. Dưới đây là chi tiết các công thức này:
2.1. Công thức tính vận tốc
Vận tốc của vật tại một thời điểm \( t \) có thể được tính bằng công thức:
- \( v \): Vận tốc tại thời điểm \( t \)
- \( v_0 \): Vận tốc ban đầu
- \( a \): Gia tốc không đổi
- \( t \): Thời gian chuyển động
2.2. Công thức tính quãng đường
Quãng đường (\( s \)) mà vật di chuyển được trong thời gian \( t \) được tính bằng công thức:
- \( s \): Quãng đường di chuyển
- \( v_0 \): Vận tốc ban đầu
- \( a \): Gia tốc
- \( t \): Thời gian chuyển động
2.3. Công thức tính gia tốc
Gia tốc (\( a \)) trong chuyển động thẳng nhanh dần đều có thể được tính bằng:
- \( a \): Gia tốc không đổi
- \( v \): Vận tốc tại thời điểm \( t \)
- \( v_0 \): Vận tốc ban đầu
- \( t \): Thời gian chuyển động
Các công thức này giúp xác định các yếu tố cơ bản trong chuyển động thẳng nhanh dần đều, từ đó có thể áp dụng vào nhiều bài toán và tình huống thực tế.

3. Ứng dụng của chuyển động thẳng nhanh dần đều
Chuyển động thẳng nhanh dần đều không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật. Dưới đây là một số ứng dụng tiêu biểu:
3.1. Trong giao thông
- Khởi hành của xe ô tô: Khi một chiếc xe ô tô khởi hành từ trạng thái đứng yên và gia tốc đều, nó sẽ có chuyển động thẳng nhanh dần đều. Việc hiểu và áp dụng các công thức chuyển động giúp lái xe tối ưu hóa việc tăng tốc và tiết kiệm nhiên liệu.
- Xe đạp và xe máy: Khi đạp xe hoặc tăng ga trên xe máy, các phương tiện này cũng thường xuyên trải qua chuyển động thẳng nhanh dần đều, đặc biệt trong các bài kiểm tra hiệu suất và an toàn.
3.2. Trong thể thao
- Chạy đường dài: Các vận động viên chạy dài cần tăng tốc đều để đạt được tốc độ tối ưu. Hiểu rõ chuyển động thẳng nhanh dần đều giúp họ điều chỉnh chiến thuật và kỹ thuật chạy hiệu quả hơn.
- Đua xe: Trong các môn đua xe, việc tối ưu hóa gia tốc để đạt tốc độ cao nhất trong thời gian ngắn là rất quan trọng. Các công thức chuyển động thẳng nhanh dần đều giúp các kỹ sư và tay đua thiết lập các chiến lược tốt nhất.
3.3. Trong kỹ thuật và thiết kế
- Thiết kế hệ thống băng tải: Các hệ thống băng tải trong nhà máy thường sử dụng chuyển động thẳng nhanh dần đều để di chuyển hàng hóa một cách liên tục và hiệu quả. Việc điều chỉnh gia tốc phù hợp giúp giảm thiểu sự rung lắc và cải thiện hiệu suất vận hành.
- Thiết bị thử nghiệm: Trong các phòng thí nghiệm, thiết bị thử nghiệm chuyển động thẳng nhanh dần đều được sử dụng để kiểm tra vật liệu và các sản phẩm dưới các điều kiện chuyển động cụ thể.
Chuyển động thẳng nhanh dần đều là một yếu tố quan trọng trong nhiều lĩnh vực, từ giao thông đến thể thao và kỹ thuật, giúp cải thiện hiệu quả và tối ưu hóa các quy trình và thiết kế.
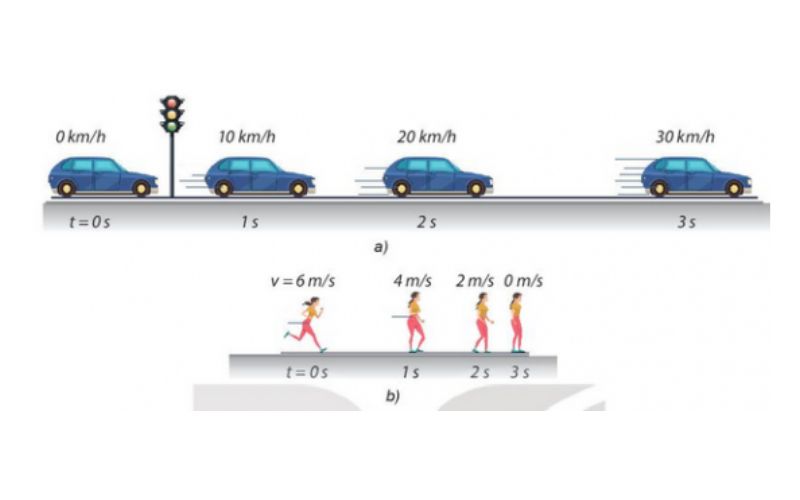
4. Ví dụ về chuyển động thẳng nhanh dần đều
Chuyển động thẳng nhanh dần đều xuất hiện trong nhiều tình huống thực tế. Dưới đây là một số ví dụ cụ thể giúp bạn hình dung rõ hơn về loại chuyển động này:
4.1. Khởi hành của ô tô
Khi một chiếc ô tô khởi động từ trạng thái đứng yên, nó thường tăng tốc đều để đạt được vận tốc tối đa. Trong trường hợp này, vận tốc của ô tô tăng đều theo thời gian với một gia tốc không đổi. Ví dụ, nếu ô tô tăng tốc từ 0 đến 60 km/h trong 10 giây, nó đang trải qua chuyển động thẳng nhanh dần đều.
4.2. Chạy đua xe thể thao
Trong các cuộc đua xe thể thao, các vận động viên cần phải tăng tốc từ vị trí xuất phát để đạt được tốc độ cao nhất trong thời gian ngắn. Khi tăng tốc đều, xe đua di chuyển với chuyển động thẳng nhanh dần đều. Ví dụ, một xe đua có thể đạt tốc độ từ 0 đến 100 km/h trong 5 giây, với gia tốc không đổi trong khoảng thời gian đó.
4.3. Trượt ván
Khi một người trượt ván từ một vị trí đứng yên và bắt đầu trượt xuống một dốc, họ thường trải qua chuyển động thẳng nhanh dần đều. Gia tốc của họ tăng đều do sự ảnh hưởng của trọng lực trên bề mặt dốc. Ví dụ, nếu người trượt ván bắt đầu từ trạng thái đứng yên và gia tốc đều khi xuống dốc, thì vận tốc của họ sẽ tăng đều theo thời gian.
4.4. Thí nghiệm trong phòng thí nghiệm
Các thí nghiệm trong phòng thí nghiệm về chuyển động của các vật thể thường sử dụng các thiết bị để tạo ra chuyển động thẳng nhanh dần đều. Ví dụ, một quả bóng rơi tự do từ một độ cao nhất định sẽ trải qua chuyển động thẳng nhanh dần đều do gia tốc trọng trường.
Những ví dụ trên giúp minh họa rõ ràng về cách chuyển động thẳng nhanh dần đều xuất hiện trong đời sống hàng ngày và các tình huống thực tế, từ giao thông đến thể thao và thí nghiệm khoa học.

5. Sự khác biệt giữa chuyển động nhanh dần đều và chậm dần đều
Chuyển động nhanh dần đều và chậm dần đều là hai loại chuyển động thường gặp, nhưng chúng có những đặc điểm khác nhau về gia tốc và sự biến đổi vận tốc.
- Chuyển động nhanh dần đều: Là chuyển động trong đó vận tốc của vật tăng dần đều theo thời gian. Gia tốc trong chuyển động này là dương, nghĩa là vận tốc của vật càng ngày càng lớn. Ví dụ, khi một chiếc ô tô bắt đầu tăng tốc từ vị trí đứng yên, nó sẽ trải qua chuyển động nhanh dần đều.
- Chuyển động chậm dần đều: Là chuyển động mà vận tốc của vật giảm dần đều theo thời gian. Gia tốc trong chuyển động này là âm, điều này có nghĩa là vật càng di chuyển thì vận tốc càng giảm. Ví dụ, khi một chiếc xe đạp phanh lại, nó sẽ trải qua chuyển động chậm dần đều.
Trong cả hai trường hợp, gia tốc là một đại lượng không đổi, nhưng hướng của gia tốc và sự thay đổi vận tốc sẽ quyết định loại chuyển động:
- Gia tốc dương \((a > 0)\): Vận tốc tăng dần, vật đang trải qua chuyển động nhanh dần đều.
- Gia tốc âm \((a < 0)\): Vận tốc giảm dần, vật đang trải qua chuyển động chậm dần đều.
Như vậy, sự khác biệt lớn nhất giữa hai loại chuyển động này là hướng của sự thay đổi vận tốc: tăng lên trong chuyển động nhanh dần đều và giảm xuống trong chuyển động chậm dần đều.