Định Nghĩa Chuyển Động Thẳng Đều: Tìm Hiểu Cơ Bản và Ứng Dụng

Chuyển động thẳng đều là dạng chuyển động mà vật di chuyển trên một đường thẳng với vận tốc không đổi theo thời gian. Trong chuyển động này, quãng đường đi được tỉ lệ thuận với thời gian chuyển động.

1. Đặc điểm của chuyển động thẳng đều

• Vận tốc \( v \) không đổi trong suốt quá trình chuyển động.
• Quãng đường \( s \) tỉ lệ thuận với thời gian chuyển động \( t \).
• Phương trình chuyển động của chất điểm trong chuyển động thẳng đều là \( x = x_0 + v \cdot t \), trong đó:
  • \( x \): tọa độ của chất điểm tại thời điểm \( t \)
  • \( x_0 \): tọa độ ban đầu
  • \( v \): vận tốc
  • \( t \): thời gian

2. Đồ thị tọa độ - thời gian trong chuyển động thẳng đều

Trong đồ thị tọa độ - thời gian của chuyển động thẳng đều, tọa độ của vật là một hàm bậc nhất của thời gian. Đường đồ thị là một đường thẳng nghiêng, với độ dốc thể hiện vận tốc của vật. Đồ thị có dạng phương trình:

3. Phương trình chuyển động thẳng đều

Phương trình chuyển động thẳng đều được sử dụng để tính toán quãng đường và thời gian của vật trong quá trình chuyển động:

• \( s = v \cdot t \)
• \( v = \frac{s}{t} \)

4. Bài tập ví dụ

Ví dụ 1: Một xe máy chuyển động thẳng đều với vận tốc \( v = 60 \, km/h \). Tính quãng đường đi được sau \( t = 2 \, h \).

• Giải: Quãng đường \( s = v \cdot t = 60 \times 2 = 120 \, km \).

Ví dụ 2: Một chất điểm chuyển động thẳng đều từ vị trí \( x_0 = 0 \, m \) với vận tốc \( v = 10 \, m/s \). Tính tọa độ của chất điểm sau \( t = 5 \, s \).

• Giải: Tọa độ \( x = x_0 + v \cdot t = 0 + 10 \times 5 = 50 \, m \).

5. Ứng dụng thực tế

Chuyển động thẳng đều xuất hiện trong nhiều tình huống thực tế, như khi một chiếc xe di chuyển trên đường với tốc độ không đổi hoặc khi tàu hỏa di chuyển trên đường ray thẳng. Hiểu rõ về chuyển động này giúp chúng ta tính toán và dự đoán được quãng đường cũng như thời gian di chuyển một cách chính xác.

6. Kết luận

Chuyển động thẳng đều là một trong những khái niệm cơ bản trong vật lý, giúp học sinh và những người quan tâm hiểu rõ hơn về cách mà các vật thể di chuyển trong thực tế. Nó không chỉ đơn giản về mặt lý thuyết mà còn có nhiều ứng dụng trong đời sống hàng ngày.

Chuyển động thẳng đều là một dạng chuyển động cơ bản trong vật lý, trong đó một vật thể di chuyển dọc theo một đường thẳng với vận tốc không đổi. Đây là một khái niệm quan trọng giúp hiểu các chuyển động cơ bản của vật thể trong không gian.

Để hiểu rõ hơn về chuyển động thẳng đều, chúng ta có thể xem xét các điểm chính sau:

• Định nghĩa: Chuyển động thẳng đều xảy ra khi một vật chuyển động với vận tốc không thay đổi về cả độ lớn và hướng. Vận tốc của vật là hằng số và không thay đổi theo thời gian.
• Quỹ đạo: Quỹ đạo của chuyển động thẳng đều là một đường thẳng. Vật thể không đổi hướng chuyển động và chỉ di chuyển dọc theo đường thẳng đó.
• Vận tốc: Vận tốc của vật trong chuyển động thẳng đều là hằng số. Ký hiệu vận tốc là \( v \) và có thể tính bằng công thức: \[ v = \frac{s}{t} \] Trong đó, \( s \) là quãng đường di chuyển và \( t \) là thời gian di chuyển.
• Gia tốc: Gia tốc trong chuyển động thẳng đều bằng 0. Điều này có nghĩa là tốc độ của vật không thay đổi theo thời gian.

Phương trình mô tả chuyển động thẳng đều là:

Trong đó:

• x là tọa độ của vật tại thời điểm t.
• x_0 là tọa độ ban đầu của vật.
• v là vận tốc của vật.
• t là thời gian kể từ khi bắt đầu chuyển động.

Để xác định quãng đường di chuyển, chúng ta sử dụng công thức:

Trong đó, \( \Delta t \) là khoảng thời gian di chuyển.

Phương trình chuyển động thẳng đều giúp chúng ta mô tả mối quan hệ giữa các yếu tố như vị trí, vận tốc và thời gian trong quá trình chuyển động của một vật thể. Dưới đây là các điểm chính về phương trình chuyển động thẳng đều:

• Phương trình cơ bản: Phương trình mô tả chuyển động thẳng đều là: \[ x = x_0 + vt \] Trong đó:
  • x là tọa độ của vật tại thời điểm t.
  • x_0 là tọa độ ban đầu của vật tại thời điểm t = 0.
  • v là vận tốc của vật, được coi là hằng số trong chuyển động thẳng đều.
  • t là thời gian kể từ lúc bắt đầu chuyển động.
• Quá trình tính toán: Để tính toán các yếu tố liên quan đến chuyển động thẳng đều, bạn cần xác định:
  • Vị trí của vật sau một khoảng thời gian nhất định.
  • Quá trình di chuyển của vật trong một khoảng thời gian cụ thể.
• Ví dụ ứng dụng: Giả sử một vật bắt đầu từ vị trí x_0 = 10 mét với vận tốc v = 5 m/s. Sau 4 giây, vị trí của vật được tính bằng phương trình: \[ x = 10 + 5 \cdot 4 = 30 \text{ mét} \] Điều này cho thấy vật đã di chuyển 20 mét trong 4 giây.

Phương trình này giúp chúng ta dễ dàng dự đoán vị trí của vật trong tương lai hoặc tính toán các yếu tố khác liên quan đến chuyển động thẳng đều.

Đồ thị chuyển động thẳng đều là một cách trực quan để biểu diễn mối quan hệ giữa các đại lượng như vị trí, vận tốc và thời gian trong quá trình chuyển động. Có hai dạng đồ thị phổ biến trong chuyển động thẳng đều: đồ thị tọa độ - thời gian và đồ thị vận tốc - thời gian.

• 1. Đồ thị tọa độ - thời gian (x - t):

  Đồ thị này biểu diễn sự thay đổi tọa độ của vật theo thời gian. Với chuyển động thẳng đều, vị trí của vật thay đổi theo phương trình:
  \[
  x = x_0 + vt
  \]
  Trong đó:
  

  
  
  • \(x\) là tọa độ của vật tại thời điểm \(t\).
  
  
  • \(x_0\) là tọa độ ban đầu của vật tại thời điểm \(t = 0\).
  
  
  • \(v\) là vận tốc của vật (hằng số).
  
  

  Trên đồ thị, tọa độ được biểu diễn trên trục tung (trục y), và thời gian trên trục hoành (trục x). Đồ thị của phương trình này là một đường thẳng có độ dốc bằng vận tốc \(v\). Độ dốc càng lớn, vận tốc của vật càng cao. Đồ thị này thể hiện rằng trong chuyển động thẳng đều, vật di chuyển với tốc độ không đổi theo thời gian.

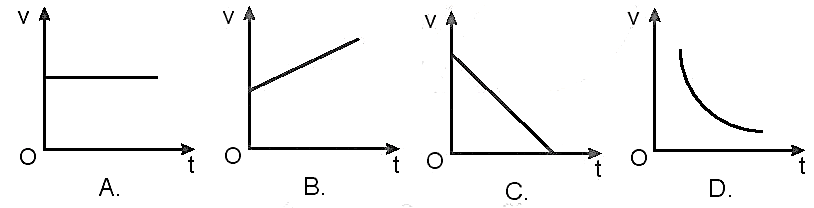
• 2. Đồ thị vận tốc - thời gian (v - t):

  Đồ thị này biểu diễn sự thay đổi vận tốc của vật theo thời gian. Trong chuyển động thẳng đều, vận tốc không thay đổi, do đó đồ thị vận tốc - thời gian là một đường thẳng nằm ngang, song song với trục thời gian. Phương trình của đồ thị này là:
  \[
  v = v_0
  \]
  Trong đó:
  

  
  
  • \(v_0\) là vận tốc không đổi của vật trong suốt quá trình chuyển động.
  
  

  Đường thẳng nằm ngang này thể hiện rằng vận tốc của vật không thay đổi, tức là vật không tăng tốc hoặc giảm tốc trong suốt quá trình chuyển động.

Thông qua các đồ thị này, chúng ta có thể dễ dàng theo dõi sự thay đổi của vị trí và vận tốc theo thời gian, giúp hiểu rõ hơn về bản chất của chuyển động thẳng đều.

Để hiểu rõ hơn về lý thuyết chuyển động thẳng đều, dưới đây là một số bài tập thực hành giúp củng cố kiến thức. Hãy giải quyết các bài tập này theo từng bước và sử dụng các công thức liên quan để tìm ra đáp án chính xác.

1. Bài tập 1: Tính quãng đường di chuyển

   Một chiếc xe chuyển động thẳng đều với vận tốc \( v = 20 \, \text{m/s} \). Hãy tính quãng đường mà xe đi được sau \( t = 5 \, \text{giây} \).

   Lời giải:

   • Sử dụng công thức: \[ s = v \cdot t \]
   • Thay các giá trị vào công thức: \[ s = 20 \cdot 5 = 100 \, \text{m} \]
   • Vậy, quãng đường xe đi được là \( 100 \, \text{m} \).
2. Bài tập 2: Xác định thời gian chuyển động

   Một vận động viên chạy với vận tốc không đổi \( v = 8 \, \text{m/s} \) trên quãng đường \( s = 400 \, \text{m} \). Hãy tính thời gian vận động viên hoàn thành quãng đường.

   Lời giải:

   • Sử dụng công thức: \[ t = \frac{s}{v} \]
   • Thay các giá trị vào công thức: \[ t = \frac{400}{8} = 50 \, \text{giây} \]
   • Vậy, thời gian vận động viên hoàn thành quãng đường là \( 50 \, \text{giây} \).
3. Bài tập 3: Vẽ đồ thị tọa độ - thời gian

   Một vật chuyển động thẳng đều từ vị trí ban đầu \( x_0 = 0 \, \text{m} \) với vận tốc \( v = 10 \, \text{m/s} \). Hãy vẽ đồ thị tọa độ - thời gian của vật trong 6 giây đầu tiên.

   Lời giải:

   • Sử dụng phương trình tọa độ: \[ x = x_0 + v \cdot t \]
   • Với \( x_0 = 0 \, \text{m} \), phương trình trở thành: \[ x = 10 \cdot t \]
   • Lập bảng giá trị để vẽ đồ thị:

   Thời gian (t) [giây]	0	1	2	3	4	5	6
   Tọa độ (x) [m]	0	10	20	30	40	50	60

   • Sử dụng bảng giá trị để vẽ đồ thị.

Chuyển động thẳng đều có rất nhiều ứng dụng trong thực tiễn và khoa học. Đây là mô hình cơ bản nhất để hiểu về cách các vật thể di chuyển với vận tốc không đổi, từ đó ứng dụng trong nhiều lĩnh vực khác nhau như giao thông, công nghiệp, và khoa học tự nhiên.

• 1. Trong giao thông:

  Chuyển động thẳng đều được ứng dụng trong việc tính toán thời gian di chuyển của các phương tiện như ô tô, tàu hỏa hay máy bay. Bằng cách sử dụng phương trình:
  \[
  s = v \cdot t
  \]
  chúng ta có thể dễ dàng xác định quãng đường di chuyển hoặc thời gian cần thiết để di chuyển một quãng đường nhất định với vận tốc không đổi.

• 2. Trong sản xuất công nghiệp:

  Các băng chuyền trong nhà máy thường hoạt động theo nguyên lý chuyển động thẳng đều, giúp vận chuyển hàng hóa từ điểm này sang điểm khác với tốc độ không đổi, đảm bảo quy trình sản xuất diễn ra liên tục và hiệu quả.

• 3. Trong khoa học vũ trụ:

  Các vệ tinh và tàu vũ trụ thường sử dụng chuyển động thẳng đều khi bay trong không gian, nơi lực cản rất nhỏ. Chúng di chuyển với vận tốc không đổi và quỹ đạo thẳng, điều này giúp các nhà khoa học dễ dàng tính toán vị trí và thời gian đến của chúng.

• 4. Trong thể thao:

  Chuyển động thẳng đều có thể được ứng dụng trong các môn thể thao như chạy bộ hoặc đua xe, nơi các vận động viên di chuyển với vận tốc không đổi để đạt thành tích tối ưu. Ví dụ, vận động viên chạy maraton thường cố gắng giữ tốc độ ổn định trong suốt quá trình thi đấu.

Nhờ vào tính đơn giản và dễ hiểu, chuyển động thẳng đều là nền tảng để học sinh, sinh viên và các nhà khoa học hiểu rõ hơn về các chuyển động phức tạp khác trong tự nhiên và kỹ thuật.