Gia Tốc Trong Chuyển Động Thẳng Đều: Khám Phá Các Nguyên Lý Cơ Bản và Ứng Dụng

Trong vật lý, gia tốc là một đại lượng vật lý đặc trưng cho sự thay đổi vận tốc của một vật trong một khoảng thời gian nhất định. Đối với chuyển động thẳng đều, gia tốc bằng không (\(a = 0\)), nghĩa là vận tốc của vật không thay đổi theo thời gian.

Công Thức Gia Tốc

Gia tốc được tính bằng công thức:

\[
a = \dfrac{\Delta v}{\Delta t}
\]

• \(\Delta v = v - v_0\): độ biến thiên vận tốc.
• \(\Delta t = t - t_0\): độ biến thiên thời gian.

Trong đó:

• \(v_0\) là vận tốc ban đầu.
• \(v\) là vận tốc tại thời điểm \(t\).

Đơn vị của gia tốc là \(\text{m/s}^2\).

Phân Loại Chuyển Động Thẳng

• Chuyển động thẳng đều: Gia tốc bằng không (\(a = 0\)), vận tốc của vật không thay đổi theo thời gian.
• Chuyển động thẳng nhanh dần đều: Gia tốc không bằng không và là hằng số (\(a \neq 0\)), vận tốc của vật tăng đều theo thời gian.
• Chuyển động thẳng chậm dần đều: Gia tốc không bằng không và là hằng số (\(a \neq 0\)), vận tốc của vật giảm đều theo thời gian.

Phương Trình Của Chuyển Động Thẳng Biến Đổi Đều

Phương trình của chuyển động thẳng biến đổi đều bao gồm:

• Phương trình vận tốc: \[ v = v_0 + a \cdot t \]
• Phương trình quãng đường: \[ S = v_0 \cdot t + \dfrac{1}{2} a \cdot t^2 \]
• Phương trình liên hệ giữa vận tốc, gia tốc và quãng đường: \[ v^2 - v_0^2 = 2aS \]

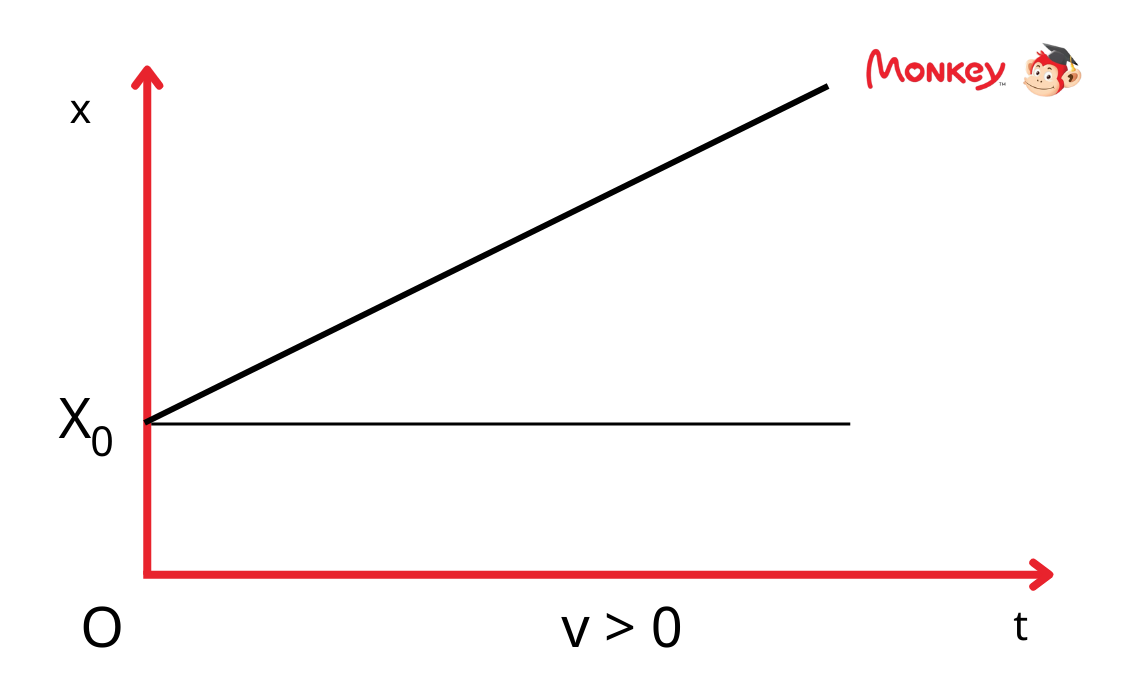
Đồ Thị Vận Tốc - Thời Gian (v - t)

Đối với chuyển động thẳng biến đổi đều, đồ thị vận tốc theo thời gian là một đường thẳng. Nếu gia tốc dương (chuyển động nhanh dần đều), đường thẳng này có độ dốc đi lên. Nếu gia tốc âm (chuyển động chậm dần đều), đường thẳng này có độ dốc đi xuống.

Ví Dụ Ứng Dụng

Ví dụ, một đoàn tàu đang chạy với vận tốc ban đầu là 36 km/h (10 m/s), sau đó hãm phanh chuyển động thẳng chậm dần đều để vào ga. Sau 2 phút (120 giây), tàu dừng lại tại sân ga. Quãng đường mà tàu đi được trong thời gian hãm phanh có thể tính bằng phương trình quãng đường:

• Tính gia tốc: \[ a = \dfrac{v - v_0}{t} = \dfrac{0 - 10}{120} = -\dfrac{1}{12} \text{m/s}^2 \]
• Quãng đường tàu đi được: \[ S = v_0 \cdot t + \dfrac{1}{2} a \cdot t^2 = 10 \cdot 120 + \dfrac{1}{2} \cdot \left(-\dfrac{1}{12}\right) \cdot (120)^2 = 600 \text{m} \]

Như vậy, quãng đường mà tàu đi được trong thời gian hãm phanh là 600 mét.

Gia tốc là một đại lượng vật lý đo lường sự thay đổi của vận tốc theo thời gian. Trong chuyển động thẳng đều, gia tốc có giá trị bằng không, tức là vận tốc của vật không thay đổi theo thời gian.

1.1 Định Nghĩa Gia Tốc

Gia tốc (\(a\)) được định nghĩa là sự thay đổi của vận tốc (\(v\)) trong một khoảng thời gian (\(\Delta t\)). Công thức tính gia tốc như sau:

\[
a = \dfrac{\Delta v}{\Delta t}
\]

• \(\Delta v = v - v_0\): Độ biến thiên của vận tốc, với \(v\) là vận tốc cuối cùng và \(v_0\) là vận tốc ban đầu.
• \(\Delta t = t - t_0\): Độ biến thiên của thời gian, với \(t\) là thời điểm cuối cùng và \(t_0\) là thời điểm ban đầu.

1.2 Đơn Vị Gia Tốc

Đơn vị của gia tốc trong hệ SI là mét trên giây bình phương (\(\text{m/s}^2\)). Điều này có nghĩa là gia tốc đo lường sự thay đổi của vận tốc theo đơn vị thời gian.

1.3 Gia Tốc Trong Chuyển Động Thẳng Đều

Trong chuyển động thẳng đều, gia tốc bằng không (\(a = 0\)). Điều này có nghĩa là:

• Vận tốc của vật không thay đổi theo thời gian.
• Đối với chuyển động thẳng đều, công thức tính vận tốc đơn giản là: \[ v = v_0 \]

1.4 Ví Dụ Minh Họa

Ví dụ, một chiếc xe ô tô đang di chuyển với vận tốc không đổi 60 km/h trên một đường thẳng. Trong trường hợp này, gia tốc của xe là:

\[
a = \dfrac{v - v_0}{\Delta t} = \dfrac{60 - 60}{\Delta t} = 0 \text{ m/s}^2
\]

Điều này cho thấy xe đang di chuyển với vận tốc ổn định và không có sự thay đổi về tốc độ.

Chuyển động thẳng là dạng chuyển động trong đó quỹ đạo của vật thể là một đường thẳng. Trong chuyển động thẳng, chúng ta có thể phân loại thành ba loại chuyển động chính:

2. Chuyển Động Thẳng Đều: Đây là loại chuyển động mà vật di chuyển với vận tốc không đổi, tức là trong những khoảng thời gian bằng nhau, vật đi được những quãng đường bằng nhau. Trong chuyển động này, gia tốc của vật luôn bằng 0. Công thức mô tả vận tốc \(v\) và quãng đường \(s\) theo thời gian \(t\) là:
3. \[
4. v = \frac{s}{t}
5. \]
6. \[
7. s = v \cdot t
8. \]
11. Chuyển Động Thẳng Nhanh Dần Đều: Loại chuyển động này xảy ra khi vật có gia tốc dương, tức là vận tốc của vật tăng dần theo thời gian. Gia tốc \(a\) của chuyển động được tính bằng công thức:
12. \[
13. a = \frac{\Delta v}{\Delta t}
14. \]
15. Vận tốc tại thời điểm \(t\) và quãng đường \(s\) đi được sau thời gian \(t\) được tính như sau:
16. \[
17. v = v_0 + a \cdot t
18. \]
19. \[
20. s = v_0 \cdot t + \frac{1}{2}a \cdot t^2
21. \]
22. Trong đó, \(v_0\) là vận tốc ban đầu của vật.
25. Chuyển Động Thẳng Chậm Dần Đều: Đây là loại chuyển động mà vận tốc của vật giảm dần theo thời gian, tức là gia tốc có giá trị âm. Công thức gia tốc \(a\), vận tốc \(v\), và quãng đường \(s\) tương tự như trong chuyển động thẳng nhanh dần đều, nhưng với \(a\) có giá trị âm:
26. \[
27. a = \frac{\Delta v}{\Delta t}
28. \]
29. \[
30. v = v_0 - a \cdot t
31. \]
32. \[
33. s = v_0 \cdot t - \frac{1}{2}a \cdot t^2
34. \]

Các loại chuyển động này là cơ sở để phân tích các dạng chuyển động phức tạp hơn và ứng dụng trong nhiều bài toán thực tế về cơ học.

Gia tốc là đại lượng thể hiện sự thay đổi vận tốc của một vật trong chuyển động. Trong chuyển động thẳng, gia tốc có thể được tính toán bằng các công thức cơ bản dựa trên các yếu tố như vận tốc, quãng đường, và thời gian. Dưới đây là các công thức và phương trình liên quan đến gia tốc trong chuyển động thẳng đều:

1. Gia Tốc Trong Chuyển Động Thẳng Đều:

   Trong chuyển động thẳng đều, gia tốc (\(a\)) là 0 vì vận tốc (\(v\)) không thay đổi theo thời gian. Do đó, công thức gia tốc là:

   \[ a = 0 \]
2. Gia Tốc Trong Chuyển Động Thẳng Nhanh Dần Đều:

   Khi vật chuyển động nhanh dần đều, gia tốc (\(a\)) có giá trị dương và có thể được tính bằng công thức:

   \[ a = \frac{v - v_0}{t} \]

   Trong đó:

   • \(v\) là vận tốc cuối cùng của vật
   • \(v_0\) là vận tốc ban đầu của vật
   • \(t\) là thời gian
3. Gia Tốc Trong Chuyển Động Thẳng Chậm Dần Đều:

   Khi vật chuyển động chậm dần đều, gia tốc (\(a\)) có giá trị âm và được tính bằng:

   \[ a = \frac{v - v_0}{t} \]

   Trong đó:

   • \(v\) là vận tốc cuối cùng của vật
   • \(v_0\) là vận tốc ban đầu của vật
   • \(t\) là thời gian

Các phương trình trên giúp tính toán gia tốc trong các dạng chuyển động thẳng cơ bản và cung cấp nền tảng để giải quyết các bài toán liên quan đến chuyển động cơ học.

Đồ thị vận tốc - thời gian là một công cụ quan trọng trong việc phân tích chuyển động thẳng đều. Nó giúp ta dễ dàng nhận biết các đặc điểm của chuyển động như vận tốc, gia tốc, và quãng đường.

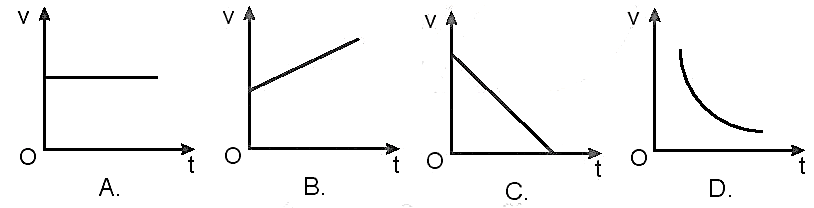
1. Đồ Thị Vận Tốc - Thời Gian trong Chuyển Động Thẳng Đều:

   Trong chuyển động thẳng đều, vận tốc không đổi theo thời gian, do đó đồ thị vận tốc - thời gian là một đường thẳng song song với trục thời gian (trục hoành). Công thức biểu diễn:

   \[ v(t) = v_0 \]

   Trong đó \(v_0\) là vận tốc không đổi.

   Đồ thị có dạng:

   Trục hoành	Thời gian (t)
   Trục tung	Vận tốc (v)
   Đường biểu diễn	Đường thẳng song song với trục thời gian

2. Phân Tích Đồ Thị:

   Phân tích đồ thị vận tốc - thời gian giúp xác định các thông số sau:

   • Vận tốc: Vận tốc của vật có thể được xác định bằng cách xem xét giá trị trên trục tung. Với chuyển động thẳng đều, giá trị này không đổi.
   • Gia tốc: Do đồ thị là một đường thẳng song song với trục thời gian, ta có thể kết luận rằng gia tốc bằng 0.
   • Quãng đường: Quãng đường di chuyển của vật trong khoảng thời gian \(\Delta t\) có thể tính bằng diện tích hình chữ nhật dưới đồ thị. Công thức tính quãng đường:
   \[ s = v_0 \times \Delta t \]
3. Ứng Dụng Thực Tế:

   Đồ thị vận tốc - thời gian được ứng dụng rộng rãi trong các bài toán thực tế để phân tích và dự đoán chuyển động của vật thể. Hiểu rõ đồ thị này giúp giải quyết các bài toán phức tạp liên quan đến động học.

Để hiểu rõ hơn về gia tốc trong chuyển động thẳng đều, chúng ta sẽ cùng xem xét một số ví dụ và bài tập thực tế. Những ví dụ này sẽ giúp bạn củng cố kiến thức và áp dụng vào các bài toán cụ thể.

1. Ví Dụ 1: Xe Chạy Trên Đường Thẳng

   Một chiếc xe di chuyển thẳng đều trên đoạn đường dài 100 km với vận tốc không đổi là 50 km/h. Hãy tính thời gian mà xe đi hết quãng đường này.

   • Lời Giải:

   Vì xe di chuyển thẳng đều, ta áp dụng công thức:

   \[ t = \frac{s}{v} \]

   Trong đó:

   • \(s = 100 \, \text{km}\) là quãng đường.
   • \(v = 50 \, \text{km/h}\) là vận tốc không đổi.

   Thời gian \(t\) được tính như sau:

   \[ t = \frac{100}{50} = 2 \, \text{giờ} \]
2. Ví Dụ 2: Người Đi Bộ

   Một người đi bộ với vận tốc không đổi 4 km/h. Sau 3 giờ, hãy tính quãng đường mà người đó đã đi được.

   • Lời Giải:

   Với chuyển động thẳng đều, quãng đường được tính bằng công thức:

   \[ s = v \times t \]

   Trong đó:

   • \(v = 4 \, \text{km/h}\) là vận tốc.
   • \(t = 3 \, \text{giờ}\) là thời gian.

   Quãng đường \(s\) được tính như sau:

   \[ s = 4 \times 3 = 12 \, \text{km} \]
3. Bài Tập Thực Hành:

   Dưới đây là một số bài tập giúp bạn luyện tập kiến thức về chuyển động thẳng đều:

   1. Một tàu hỏa di chuyển với vận tốc 60 km/h trên đoạn đường dài 180 km. Hãy tính thời gian cần thiết để tàu đi hết đoạn đường này.
   2. Một máy bay di chuyển thẳng đều với vận tốc 800 km/h. Sau 2 giờ, máy bay đã đi được quãng đường bao nhiêu?
   3. Một người đạp xe từ điểm A đến điểm B với vận tốc 15 km/h. Quãng đường từ A đến B là 45 km. Tính thời gian mà người đó cần để hoàn thành chuyến đi.

Để hiểu rõ hơn về gia tốc trong chuyển động thẳng đều và áp dụng kiến thức vào thực tế, bạn có thể tham khảo các tài liệu và nguồn học tập sau:

• Sách Giáo Khoa:

  • Sách "Cơ học cơ bản" của tác giả Nguyễn Đình Dương và Lê Thị Hồng Hà.

  • Sách "Đại số và Giải tích cơ bản" của tác giả Trần Văn Sơn và Nguyễn Thị Thu Trang.

• Tài Liệu Học Thuật Trực Tuyến:

• Video Hướng Dẫn:

• Trang Web Học Tập: