Chuyển Động Thẳng Đều Công Thức: Hướng Dẫn Chi Tiết và Ứng Dụng Thực Tiễn

Chuyển động thẳng đều là một dạng chuyển động trong đó vật di chuyển trên quỹ đạo thẳng với vận tốc không đổi, nghĩa là quãng đường vật đi được trong các khoảng thời gian bằng nhau sẽ như nhau.

1. Định nghĩa

Chuyển động thẳng đều được định nghĩa là chuyển động trong đó:

• Quỹ đạo của vật là đường thẳng.
• Vận tốc của vật không đổi về phương, chiều và độ lớn.
• Gia tốc của vật bằng 0.

2. Công thức tính quãng đường và vận tốc

Trong chuyển động thẳng đều, các công thức cơ bản được sử dụng bao gồm:

• Vận tốc: \[ v = \frac{s}{t} \] Trong đó:
  • \(v\): vận tốc (m/s hoặc km/h)
  • \(s\): quãng đường đi được (m hoặc km)
  • \(t\): thời gian đi hết quãng đường (s hoặc h)
• Quãng đường: \[ s = v \cdot t \] Trong đó:
  • \(v\): vận tốc của vật (m/s hoặc km/h)
  • \(t\): thời gian (s hoặc h)

3. Phương trình chuyển động

Phương trình chuyển động thẳng đều được viết dưới dạng:

• \(x\): tọa độ của vật tại thời điểm \(t\)
• \(x_0\): tọa độ ban đầu của vật tại thời điểm \(t_0\)
• \(t_0\): thời điểm ban đầu

Trong thực tế, để đơn giản hóa, chúng ta thường chọn \(t_0 = 0\), do đó phương trình sẽ trở thành:

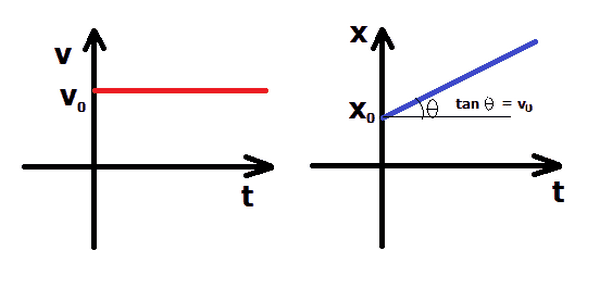
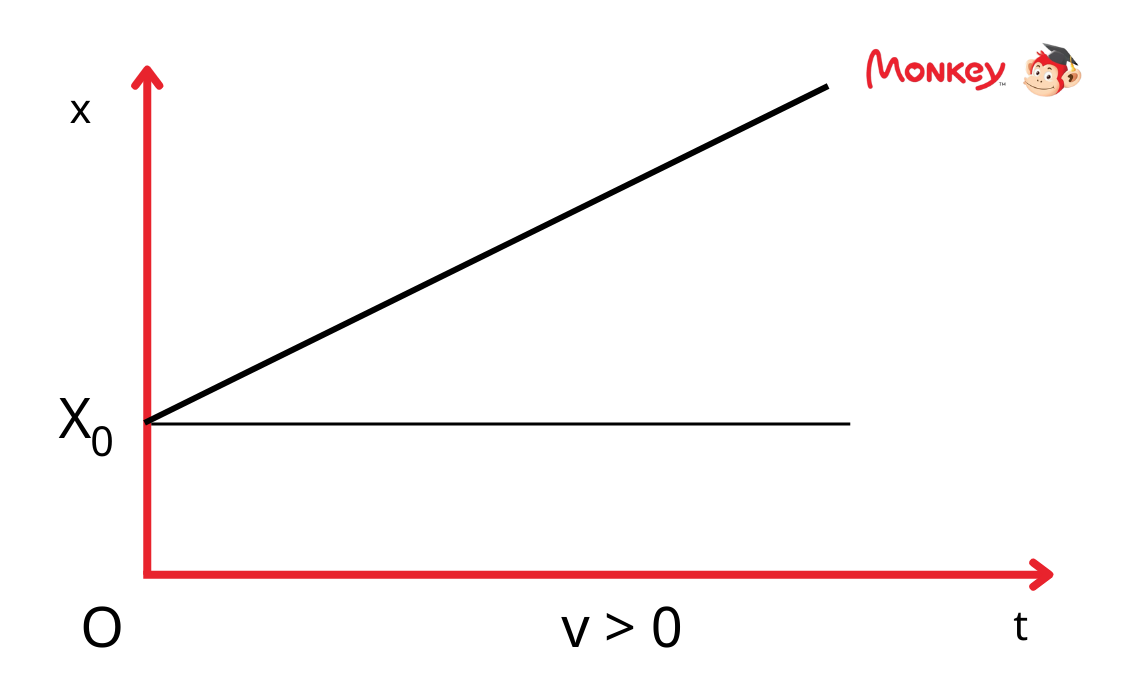
4. Đồ thị tọa độ - thời gian

Đồ thị tọa độ theo thời gian của chuyển động thẳng đều là một đường thẳng có độ dốc không đổi. Phương trình đồ thị có dạng:

Độ dốc của đồ thị chính là vận tốc của vật. Nếu vận tốc dương, đồ thị sẽ có xu hướng đi lên, còn nếu vận tốc âm, đồ thị sẽ đi xuống.

5. Ví dụ minh họa

Giả sử một xe đạp bắt đầu chuyển động thẳng đều với vận tốc 10 km/h từ vị trí cách điểm gốc 5 km. Phương trình chuyển động của xe đạp là:

Ở thời điểm \(t = 2\) giờ, tọa độ của xe đạp sẽ là:

Vậy sau 2 giờ, xe đạp sẽ cách điểm gốc 25 km.

Hy vọng các công thức và ví dụ trên sẽ giúp bạn hiểu rõ hơn về chuyển động thẳng đều.

Chuyển động thẳng đều là một dạng chuyển động cơ bản trong vật lý, được đặc trưng bởi việc chất điểm di chuyển trên một quỹ đạo thẳng với vận tốc không thay đổi.

• Khái Niệm: Chuyển động thẳng đều xảy ra khi một vật di chuyển theo một đường thẳng và tốc độ của nó không thay đổi theo thời gian.
• Đặc Điểm:
  • Quỹ Đạo: Đường đi của vật là một đường thẳng.
  • Vận Tốc: Vận tốc của vật giữ nguyên, không thay đổi về phương, chiều và độ lớn.
  • Gia Tốc: Gia tốc của vật bằng 0 vì vận tốc không thay đổi.
• Phương Trình Chuyển Động:

  Phương trình tổng quát của chuyển động thẳng đều được viết như sau:

  \[ x = x_0 + v \cdot t \]

  Trong đó:

  • x: Tọa độ của vật tại thời điểm \(t\).
  • x_0: Tọa độ ban đầu của vật tại thời điểm \(t_0\).
  • v: Vận tốc của vật.
  • t: Thời gian đã trôi qua.
• Ứng Dụng: Chuyển động thẳng đều thường được sử dụng để mô tả các chuyển động đơn giản trong đời sống hàng ngày như xe chạy trên đường thẳng với tốc độ không đổi.

Chuyển động thẳng đều có một số công thức cơ bản để tính toán quãng đường, vận tốc và tọa độ của vật. Dưới đây là các công thức chính được sử dụng trong chuyển động thẳng đều:

• Công Thức Tính Vận Tốc:

  Vận tốc (v) được tính bằng thương số giữa quãng đường đi được (s) và thời gian (t) để đi hết quãng đường đó:

  \[ v = \frac{s}{t} \]

  Trong đó:

  • v: Vận tốc (m/s hoặc km/h)
  • s: Quãng đường đi được (m hoặc km)
  • t: Thời gian (s hoặc h)
• Công Thức Tính Quãng Đường:

  Quãng đường (s) được tính bằng tích của vận tốc (v) và thời gian (t):

  \[ s = v \cdot t \]

  Trong đó:

  • s: Quãng đường đi được (m hoặc km)
  • v: Vận tốc của vật (m/s hoặc km/h)
  • t: Thời gian (s hoặc h)
• Công Thức Tính Tọa Độ:

  Phương trình chuyển động thẳng đều cho biết tọa độ (x) của vật tại thời điểm t:

  \[ x = x_0 + v \cdot t \]

  Trong đó:

  • x: Tọa độ của vật tại thời điểm \(t\)
  • x_0: Tọa độ ban đầu của vật tại thời điểm \(t_0\)
  • v: Vận tốc của vật
  • t: Thời gian đã trôi qua

Những công thức này giúp chúng ta dễ dàng tính toán các yếu tố liên quan đến chuyển động thẳng đều và áp dụng vào các bài toán vật lý và trong thực tế.

Chuyển động thẳng đều có nhiều ứng dụng trong đời sống hàng ngày và trong các lĩnh vực kỹ thuật khác nhau. Dưới đây là một số ứng dụng chính:

• Trong Giao Thông:

  Chuyển động thẳng đều mô tả các phương tiện di chuyển với vận tốc không đổi trên các đoạn đường thẳng. Ví dụ, khi một ô tô di chuyển trên đường cao tốc với vận tốc ổn định, nó thực hiện chuyển động thẳng đều. Điều này giúp dễ dàng dự đoán thời gian và quãng đường đi được.

• Trong Thí Nghiệm Vật Lý:

  Chuyển động thẳng đều được sử dụng trong nhiều thí nghiệm vật lý để kiểm tra các nguyên lý cơ bản và công thức tính toán. Nó giúp các nhà nghiên cứu xác định các đặc tính cơ bản của vật chuyển động và ứng dụng trong các mô hình lý thuyết.

• Trong Kỹ Thuật:

  Các hệ thống cơ khí, chẳng hạn như băng chuyền trong nhà máy, hoạt động với chuyển động thẳng đều để đảm bảo các sản phẩm di chuyển liên tục và đồng đều. Việc hiểu và áp dụng chuyển động thẳng đều giúp tối ưu hóa hiệu suất và độ chính xác của các hệ thống này.

• Trong Giảng Dạy:

  Chuyển động thẳng đều là một khái niệm cơ bản trong giáo dục vật lý, giúp học sinh và sinh viên hiểu các nguyên lý cơ bản của chuyển động và ứng dụng trong các bài tập và bài thi. Nó cung cấp nền tảng vững chắc cho việc học các dạng chuyển động phức tạp hơn.

Những ứng dụng này cho thấy sự quan trọng và tính thiết thực của chuyển động thẳng đều trong các lĩnh vực khác nhau, từ giao thông đến nghiên cứu và kỹ thuật.

Dưới đây là một số bài tập liên quan đến chuyển động thẳng đều cùng với lời giải chi tiết, giúp bạn hiểu rõ hơn về cách áp dụng các công thức trong thực tế.

• Bài Tập 1: Một ô tô di chuyển thẳng đều với vận tốc \( v = 20 \, \text{m/s} \) trong thời gian \( t = 5 \, \text{s} \). Tính quãng đường mà ô tô đã đi được.

  Lời giải:

  Áp dụng công thức tính quãng đường:

  \[ s = v \cdot t \]

  Thay các giá trị vào công thức:

  \[ s = 20 \, \text{m/s} \times 5 \, \text{s} = 100 \, \text{m} \]

  Vậy quãng đường ô tô đi được là 100m.

• Bài Tập 2: Một vật bắt đầu di chuyển từ vị trí \( x_0 = 10 \, \text{m} \) với vận tốc \( v = 5 \, \text{m/s} \). Hỏi sau 8 giây, vật ở vị trí nào?

  Lời giải:

  Áp dụng phương trình tọa độ:

  \[ x = x_0 + v \cdot t \]

  Thay các giá trị vào công thức:

  \[ x = 10 \, \text{m} + 5 \, \text{m/s} \times 8 \, \text{s} = 50 \, \text{m} \]

  Vậy sau 8 giây, vật sẽ ở vị trí \( x = 50 \, \text{m} \).

• Bài Tập 3: Một người đi bộ với vận tốc \( v = 1.5 \, \text{m/s} \). Tính thời gian để người này đi được quãng đường 450m.

  Lời giải:

  Áp dụng công thức tính thời gian:

  \[ t = \frac{s}{v} \]

  Thay các giá trị vào công thức:

  \[ t = \frac{450 \, \text{m}}{1.5 \, \text{m/s}} = 300 \, \text{s} \]

  Vậy người này cần 300 giây để đi được quãng đường 450m.

Các bài tập trên giúp củng cố kiến thức về chuyển động thẳng đều, bao gồm cách tính quãng đường, vận tốc và thời gian.

Phần này sẽ cung cấp những kiến thức mở rộng về chuyển động thẳng đều, giúp bạn hiểu sâu hơn về các khái niệm vật lý liên quan và cách áp dụng vào thực tế.

5.1. Liên Hệ Với Các Khái Niệm Vật Lý Khác

• Chuyển động thẳng biến đổi đều: Khác với chuyển động thẳng đều, ở chuyển động thẳng biến đổi đều, vận tốc của vật thay đổi đều đặn theo thời gian, thường là do tác dụng của lực.
• Gia tốc: Gia tốc trong chuyển động thẳng đều bằng 0 vì vận tốc không thay đổi. Nhưng với các chuyển động khác như chuyển động thẳng nhanh dần hoặc chậm dần đều, gia tốc là một đại lượng quan trọng để đo lường sự thay đổi vận tốc.
• Chuyển động tròn đều: Khái niệm tương tự với chuyển động thẳng đều, nhưng quỹ đạo của vật là đường tròn thay vì đường thẳng. Vận tốc của vật có độ lớn không đổi nhưng hướng vận tốc luôn thay đổi theo quỹ đạo tròn.

5.2. Các Sai Lầm Thường Gặp Khi Tính Toán

• Quên đơn vị của vận tốc: Khi tính quãng đường hoặc vận tốc, nhiều người thường quên kiểm tra đơn vị (m/s hoặc km/h). Điều này dẫn đến sai số trong kết quả.
• Nhầm lẫn giữa vận tốc trung bình và vận tốc tức thời: Vận tốc trung bình là thương số giữa quãng đường đi được và thời gian chuyển động, trong khi vận tốc tức thời chỉ xét tại một thời điểm cụ thể.
• Không xác định đúng hệ tọa độ: Đối với bài toán phức tạp, việc chọn đúng hệ tọa độ là rất quan trọng để có được phương trình chuyển động đúng.

5.3. Cập Nhật Các Phương Pháp Tính Mới

• Sử dụng phần mềm mô phỏng: Các phần mềm vật lý hiện đại giúp mô phỏng chuyển động của các vật thể một cách trực quan, giúp học sinh và sinh viên dễ dàng hình dung và hiểu rõ hơn về chuyển động thẳng đều và các khái niệm liên quan.
• Phương pháp đo đạc kỹ thuật số: Hiện nay, các thiết bị đo đạc điện tử cho phép tính toán chính xác hơn về thời gian và quãng đường, giúp tăng độ tin cậy trong việc nghiên cứu và áp dụng vào thực tiễn.

Để nắm vững kiến thức về chuyển động thẳng đều, dưới đây là một số tài liệu và nguồn tham khảo hữu ích:

• Sách và Tài Liệu Vật Lý:
• Giáo trình Vật Lý 10 – Cuốn sách cơ bản cung cấp kiến thức về chuyển động thẳng đều, công thức tính quãng đường và vận tốc, kèm theo các ví dụ minh họa chi tiết.
• Các chuyên đề Vật Lý nâng cao – Dành cho học sinh muốn tìm hiểu sâu hơn về các bài toán phức tạp liên quan đến chuyển động thẳng đều.
• Các Trang Web Học Tập Hữu Ích:
• – Cung cấp bài giảng và hướng dẫn về phương trình chuyển động, đồ thị tọa độ - thời gian và các dạng bài tập thực hành.
• – Trang web với nhiều bài học lý thuyết về chuyển động thẳng đều, kèm các bài tập thực hành và hướng dẫn giải chi tiết.
• Video Hướng Dẫn và Bài Giảng:
• – Kênh YouTube cung cấp các video bài giảng về chuyển động thẳng đều với các ví dụ cụ thể và đồ thị minh họa.
• – Nơi chia sẻ các video giải bài tập và đồ thị chuyển động từ cơ bản đến nâng cao.