Chủ đề chuyển động thẳng nhanh dần đều có gia tốc: Chuyển động thẳng nhanh dần đều có gia tốc là một khái niệm quan trọng trong vật lý, đặc biệt là trong các bài học về cơ học. Bài viết này sẽ giúp bạn nắm bắt các công thức cơ bản, cách tính toán gia tốc và vận tốc, cũng như những ứng dụng thực tiễn của chuyển động này trong đời sống và kỹ thuật. Khám phá ngay để hiểu sâu hơn về hiện tượng này!
Mục lục
Chuyển Động Thẳng Nhanh Dần Đều Có Gia Tốc
Chuyển động thẳng nhanh dần đều là một trong những loại chuyển động cơ bản được học trong Vật lý. Đây là chuyển động mà vật di chuyển theo quỹ đạo đường thẳng và độ lớn của vận tốc tăng đều theo thời gian. Gia tốc trong trường hợp này là đại lượng vật lý đặc trưng cho sự biến thiên của vận tốc theo thời gian, và nó có giá trị không đổi.
1. Định nghĩa về chuyển động thẳng nhanh dần đều
Chuyển động thẳng nhanh dần đều là chuyển động theo một đường thẳng, trong đó độ lớn của vận tốc tăng đều theo thời gian. Gia tốc trong chuyển động này có giá trị dương và không thay đổi.
Công thức của chuyển động thẳng nhanh dần đều:
- Phương trình vận tốc: \( v = v_0 + at \)
- Phương trình tọa độ: \( x = x_0 + v_0t + \frac{1}{2}at^2 \)
- Hệ thức độc lập thời gian: \( v^2 = v_0^2 + 2a\Delta x \)
2. Gia tốc của chuyển động thẳng nhanh dần đều
Gia tốc \(a\) là đại lượng đặc trưng cho sự thay đổi vận tốc theo thời gian, được xác định bởi:
\[ a = \frac{\Delta v}{\Delta t} = \frac{v - v_0}{t} \]
- Gia tốc có đơn vị là \( \text{m/s}^2 \).
- Nếu \( a > 0 \), vận tốc tăng đều (chuyển động nhanh dần đều).
3. Các đại lượng trong chuyển động thẳng nhanh dần đều
| Đại lượng | Ký hiệu | Đơn vị |
|---|---|---|
| Gia tốc | \(a\) | \( \text{m/s}^2 \) |
| Vận tốc ban đầu | \(v_0\) | \( \text{m/s} \) |
| Vận tốc tại thời điểm \(t\) | \(v\) | \( \text{m/s} \) |
| Thời gian | \(t\) | \( \text{s} \) |
| Quãng đường | \(x\) | \( \text{m} \) |
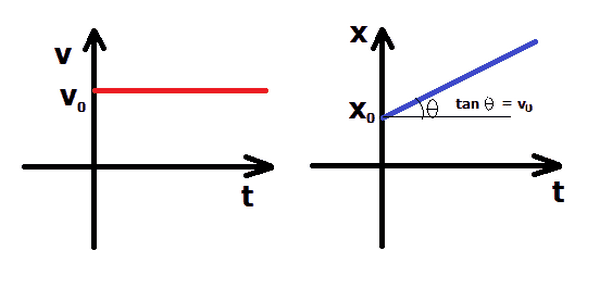
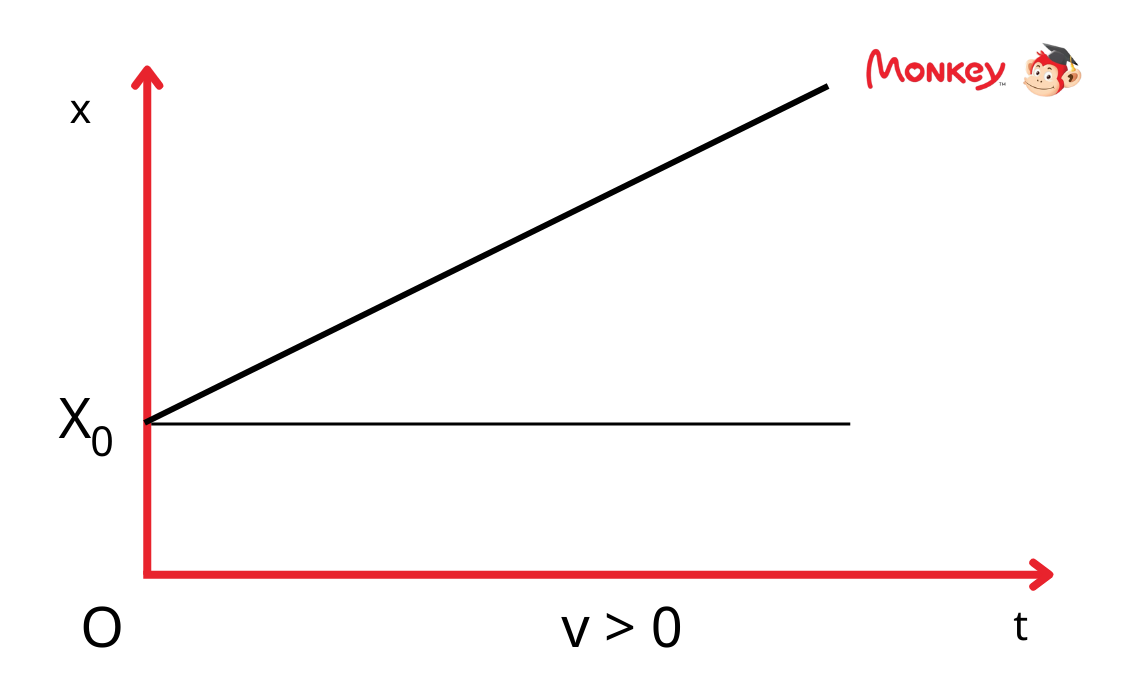
4. Đồ thị của chuyển động thẳng nhanh dần đều
Có 2 loại đồ thị thường gặp trong chuyển động thẳng nhanh dần đều:
- Đồ thị vận tốc - thời gian: Đây là một đường thẳng dốc lên. Độ dốc của đường thẳng chính là giá trị của gia tốc \(a\).
- Đồ thị quãng đường - thời gian: Đây là một parabol, với quãng đường tăng dần nhanh hơn theo thời gian do vận tốc liên tục tăng.
5. Ví dụ về chuyển động thẳng nhanh dần đều
Ví dụ về chuyển động thẳng nhanh dần đều: Một ô tô khởi hành từ trạng thái nghỉ, sau 10 giây đạt vận tốc 20 m/s. Tính gia tốc của ô tô và quãng đường mà ô tô đi được trong 10 giây đầu tiên.
- Gia tốc của ô tô: \( a = \frac{v - v_0}{t} = \frac{20 - 0}{10} = 2 \, \text{m/s}^2 \)
- Quãng đường đi được: \( x = v_0 t + \frac{1}{2} a t^2 = 0 + \frac{1}{2} \times 2 \times 10^2 = 100 \, \text{m} \)
Chuyển động thẳng nhanh dần đều là một kiến thức cơ bản nhưng rất quan trọng trong Vật lý, giúp học sinh hiểu rõ hơn về mối quan hệ giữa gia tốc, vận tốc và quãng đường.
.png)
1. Khái niệm cơ bản về chuyển động thẳng nhanh dần đều
Chuyển động thẳng nhanh dần đều là một dạng chuyển động trong đó một vật di chuyển theo đường thẳng và gia tốc của nó là không đổi. Trong trường hợp này, độ lớn của vận tốc của vật tăng đều theo thời gian. Đây là một trong những khái niệm cơ bản trong vật lý và có ứng dụng rộng rãi trong các tình huống thực tế và bài tập học thuật.
1.1. Định nghĩa
Chuyển động thẳng nhanh dần đều được định nghĩa là chuyển động của một vật với gia tốc không đổi và vận tốc của nó tăng đều theo thời gian. Gia tốc \(a\) là đại lượng đặc trưng cho sự thay đổi của vận tốc và có giá trị không đổi trong toàn bộ quá trình chuyển động.
1.2. Công thức cơ bản
- Phương trình vận tốc: \[ v = v_0 + at \]
- Phương trình quãng đường: \[ s = v_0t + \frac{1}{2}at^2 \]
- Hệ thức liên hệ giữa vận tốc và quãng đường: \[ v^2 = v_0^2 + 2as \]
1.3. Ví dụ minh họa
Giả sử một ô tô bắt đầu từ trạng thái nghỉ và có gia tốc 2 m/s². Sau 5 giây, vận tốc của ô tô sẽ là:
\[ v = 0 + 2 \times 5 = 10 \, \text{m/s} \]
Quãng đường mà ô tô đi được trong 5 giây là:
\[ s = 0 \times 5 + \frac{1}{2} \times 2 \times 5^2 = 0 + 25 = 25 \, \text{m} \]
1.4. Đặc điểm gia tốc
Gia tốc trong chuyển động thẳng nhanh dần đều có đặc điểm sau:
- Gia tốc là đại lượng không đổi.
- Gia tốc có cùng phương và chiều với vận tốc.
- Gia tốc có đơn vị là \(\text{m/s}^2\).
1.5. Đồ thị chuyển động
Đồ thị của chuyển động thẳng nhanh dần đều bao gồm:
- Đồ thị vận tốc - thời gian: Đường thẳng dốc lên với độ dốc bằng giá trị của gia tốc.
- Đồ thị quãng đường - thời gian: Đường parabol, thể hiện sự gia tăng quãng đường theo thời gian.
1.6. Ứng dụng trong thực tế
Chuyển động thẳng nhanh dần đều xuất hiện trong nhiều tình huống thực tế như:
- Ô tô tăng tốc khi khởi hành từ trạng thái nghỉ.
- Vật thể rơi tự do dưới tác dụng của trọng lực (trong môi trường không có lực cản).
- Các bài tập và thí nghiệm trong giáo dục vật lý.
2. Các công thức cơ bản trong chuyển động thẳng nhanh dần đều
2.1. Phương trình vận tốc
Phương trình vận tốc trong chuyển động thẳng nhanh dần đều cho biết vận tốc của vật tại thời điểm bất kỳ. Công thức được biểu diễn như sau:
\( v = v_0 + at \)
- v: Vận tốc tại thời điểm t
- v_0: Vận tốc ban đầu
- a: Gia tốc
- t: Thời gian
2.2. Phương trình quãng đường
Phương trình quãng đường mô tả quãng đường vật đã đi được trong thời gian t. Công thức là:
\( s = v_0t + \frac{1}{2}at^2 \)
- s: Quãng đường đi được
- v_0: Vận tốc ban đầu
- a: Gia tốc
- t: Thời gian
2.3. Hệ thức liên hệ giữa vận tốc và quãng đường
Đây là công thức giúp liên kết vận tốc với quãng đường đã đi được. Công thức là:
\( v^2 - v_0^2 = 2as \)
- v: Vận tốc tại thời điểm cuối
- v_0: Vận tốc ban đầu
- a: Gia tốc
- s: Quãng đường đi được

3. Các đại lượng liên quan trong chuyển động thẳng nhanh dần đều
3.1. Vận tốc tức thời
Vận tốc tức thời tại một thời điểm bất kỳ cho biết độ nhanh chậm của vật tại thời điểm đó. Vận tốc tức thời trong chuyển động thẳng nhanh dần đều được xác định bằng phương trình:
\[ v = v_0 + at \]
Trong đó:
- \(v_0\): Vận tốc ban đầu (m/s).
- \(a\): Gia tốc (m/s²).
- \(t\): Thời gian chuyển động (s).
Vận tốc tức thời tăng đều theo thời gian trong chuyển động nhanh dần đều, tức là tốc độ vật ngày càng nhanh hơn.
3.2. Gia tốc và vai trò của gia tốc
Gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi của vận tốc theo thời gian. Trong chuyển động thẳng nhanh dần đều, gia tốc là một đại lượng không đổi và được tính theo công thức:
\[ a = \frac{\Delta v}{\Delta t} \]
Trong đó:
- \(\Delta v\): Độ biến thiên vận tốc (m/s).
- \(\Delta t\): Khoảng thời gian thay đổi vận tốc (s).
Gia tốc dương đồng nghĩa với việc vật chuyển động nhanh dần đều, tức là vận tốc của vật tăng lên trong suốt quá trình chuyển động.
3.3. Quãng đường đi được
Quãng đường trong chuyển động thẳng nhanh dần đều được tính theo công thức:
\[ s = v_0t + \frac{1}{2}at^2 \]
Trong đó:
- \(s\): Quãng đường đi được (m).
- \(v_0\): Vận tốc ban đầu (m/s).
- \(t\): Thời gian chuyển động (s).
- \(a\): Gia tốc (m/s²).
Công thức này giúp tính toán quãng đường vật đi được trong khoảng thời gian nhất định, với giả định gia tốc không đổi. Khi gia tốc dương, vật sẽ đi nhanh hơn theo thời gian và quãng đường càng lúc càng dài hơn.

5. Bài tập và ứng dụng trong thực tế
5.1. Bài tập ví dụ
Dưới đây là một số bài tập về chuyển động thẳng nhanh dần đều giúp bạn hiểu rõ hơn về lý thuyết:
- Bài tập 1: Một ô tô bắt đầu chuyển động từ trạng thái nghỉ và sau 5 giây đạt được vận tốc 20 m/s. Tính gia tốc của ô tô và quãng đường nó đi được trong khoảng thời gian này.
- Bài tập 2: Một vật bắt đầu chuyển động nhanh dần đều từ vận tốc ban đầu là 10 m/s và sau khi đi được 100m thì đạt vận tốc 30 m/s. Tìm gia tốc của vật.
Lời giải:
Sử dụng công thức:
Vận tốc: \( v = v_0 + at \)
Với \( v_0 = 0 \), ta có: \( a = \frac{v}{t} = \frac{20}{5} = 4 \, m/s^2 \)
Quãng đường: \( s = v_0t + \frac{1}{2}at^2 = \frac{1}{2} \times 4 \times 5^2 = 50 \, m \)
Lời giải:
Dùng công thức liên hệ giữa vận tốc và quãng đường:
\( v^2 - v_0^2 = 2as \)
Thay số vào: \( 30^2 - 10^2 = 2a \times 100 \)
Ta có: \( a = 4 \, m/s^2 \)
5.2. Ứng dụng trong đời sống
Chuyển động thẳng nhanh dần đều có rất nhiều ứng dụng trong thực tế, từ các phương tiện giao thông cho đến các quá trình sản xuất công nghiệp:
- Giao thông: Các phương tiện như ô tô, tàu hỏa thường sử dụng chuyển động thẳng nhanh dần đều khi bắt đầu di chuyển từ trạng thái nghỉ. Tính toán về gia tốc và quãng đường giúp tối ưu hóa việc điều khiển vận tốc của phương tiện, đảm bảo an toàn và tiết kiệm năng lượng.
- Ứng dụng trong kỹ thuật: Trong sản xuất, các băng chuyền hoặc hệ thống máy móc có thể hoạt động theo cơ chế chuyển động nhanh dần đều để đảm bảo hiệu quả làm việc tối đa trong thời gian ngắn.
- Trong thể thao: Ở các môn đua xe hay chạy nước rút, vận động viên cần đạt tốc độ tối đa trong thời gian ngắn nhất, việc hiểu và áp dụng nguyên lý chuyển động nhanh dần đều giúp các huấn luyện viên và vận động viên xây dựng chiến thuật phù hợp.