Chủ đề quỹ đạo của chuyển động thẳng đều là đường thẳng: Quỹ đạo của chuyển động thẳng đều là đường thẳng là một chủ đề quan trọng trong vật lý cơ bản. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm, đặc điểm, và các ứng dụng thực tiễn của chuyển động thẳng đều. Khám phá những điều thú vị về cách vật thể di chuyển trong không gian với vận tốc không đổi.
Mục lục
Chuyển động thẳng đều
Chuyển động thẳng đều là một dạng chuyển động trong đó một vật di chuyển theo quỹ đạo thẳng và có vận tốc không thay đổi theo thời gian. Đặc điểm quan trọng của chuyển động này là:
- Quỹ đạo là một đường thẳng.
- Vận tốc của vật không thay đổi (vận tốc không đổi về phương, chiều và độ lớn).
- Gia tốc của vật bằng 0.
Công thức tính vận tốc trong chuyển động thẳng đều:
Công thức tính vận tốc của chuyển động thẳng đều là:
\[
v = \frac{s}{t}
\]
Trong đó:
- \(v\): vận tốc của vật (m/s).
- \(s\): quãng đường vật đi được (m).
- \(t\): thời gian để vật đi hết quãng đường \(s\) (s).
Phương trình chuyển động thẳng đều
Phương trình tọa độ của chuyển động thẳng đều được biểu diễn dưới dạng:
\[
x = x_0 + v(t - t_0)
\]
Trong đó:
- \(x\): tọa độ của vật tại thời điểm \(t\).
- \(x_0\): tọa độ ban đầu của vật tại thời điểm \(t_0\).
- \(v\): vận tốc không đổi của vật.
- \(t_0\): gốc thời gian (thường chọn \(t_0 = 0\) để đơn giản).
Quãng đường đi được sau thời gian \(\Delta t\)
Quãng đường mà vật đi được sau khoảng thời gian \(\Delta t\) là:
\[
s = |v| \cdot \Delta t
\]
Nếu vật chuyển động không đổi chiều, độ dời sẽ bằng quãng đường đã đi, tức là:
\[
\Delta x = s
\]
Đồ thị tọa độ - thời gian của chuyển động thẳng đều
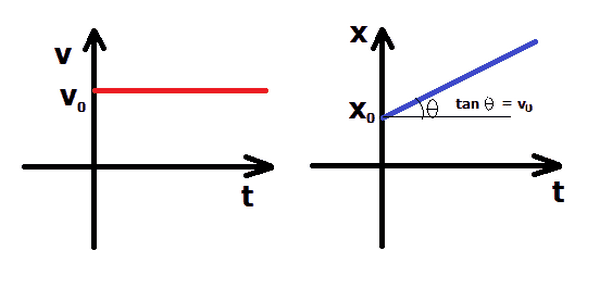
Đồ thị tọa độ - thời gian của chuyển động thẳng đều là một đường thẳng có độ dốc tỉ lệ thuận với vận tốc:
\[
\text{tan} \theta = v
\]
Nếu vận tốc \(v > 0\), đồ thị sẽ có độ dốc hướng lên. Ngược lại, nếu \(v < 0\), đồ thị sẽ có độ dốc hướng xuống.
Ví dụ minh họa
Xét một xe ô tô chuyển động thẳng đều với vận tốc 72 km/h, bắt đầu từ vị trí \(x_0 = 0\) km tại thời điểm \(t_0 = 0\). Phương trình chuyển động của xe ô tô này sẽ là:
\[
x = 72t
\]
Đây là phương trình biểu diễn mối quan hệ giữa tọa độ \(x\) và thời gian \(t\) của xe trong chuyển động thẳng đều.
Tóm lại, trong chuyển động thẳng đều, vật di chuyển theo một đường thẳng với vận tốc không đổi, và có nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày như xe chạy trên đường thẳng mà không thay đổi vận tốc.

.png)
I. Khái niệm chuyển động thẳng đều
Chuyển động thẳng đều là chuyển động trong đó một vật di chuyển theo một quỹ đạo thẳng và có vận tốc không thay đổi theo thời gian. Điều này có nghĩa là:
- Quỹ đạo của chuyển động là một đường thẳng.
- Vận tốc của vật không đổi, tức là không tăng hay giảm trong suốt quá trình chuyển động.
- Gia tốc của vật bằng 0 vì vận tốc không thay đổi.
Trong chuyển động thẳng đều, công thức cơ bản mô tả mối quan hệ giữa quãng đường, vận tốc và thời gian là:
\[
v = \frac{s}{t}
\]
Trong đó:
- \(v\): Vận tốc của vật (m/s).
- \(s\): Quãng đường vật di chuyển (m).
- \(t\): Thời gian vật di chuyển trên quãng đường \(s\) (s).
Chuyển động thẳng đều có nhiều ứng dụng trong đời sống, chẳng hạn như xe di chuyển trên đường thẳng với tốc độ không đổi hay các vật thể di chuyển trên băng chuyền trong nhà máy.
II. Phương trình chuyển động thẳng đều
Phương trình chuyển động thẳng đều mô tả mối quan hệ giữa tọa độ, vận tốc và thời gian của một vật di chuyển theo quỹ đạo thẳng với vận tốc không đổi. Phương trình tổng quát cho chuyển động thẳng đều được biểu diễn như sau:
\[
x = x_0 + v \cdot t
\]
Trong đó:
- \(x\): Tọa độ của vật tại thời điểm \(t\) (m).
- \(x_0\): Tọa độ ban đầu của vật tại thời điểm \(t_0\) (m).
- \(v\): Vận tốc không đổi của vật (m/s).
- \(t\): Thời gian chuyển động (s).
Phương trình này thể hiện rằng tọa độ \(x\) của vật thay đổi tuyến tính theo thời gian \(t\), với hệ số góc là vận tốc \(v\). Nếu vận tốc \(v > 0\), vật chuyển động theo chiều dương của trục tọa độ. Nếu \(v < 0\), vật chuyển động theo chiều âm.
Ví dụ, nếu một vật bắt đầu chuyển động từ vị trí \(x_0 = 0\) với vận tốc \(v = 5 \, \text{m/s}\), thì sau 10 giây, tọa độ của vật sẽ là:
\[
x = 0 + 5 \cdot 10 = 50 \, \text{m}
\]
Điều này có nghĩa là sau 10 giây, vật đã di chuyển được 50 mét theo quỹ đạo thẳng đều với vận tốc không đổi.

III. Đồ thị tọa độ - thời gian
Đồ thị tọa độ - thời gian là biểu diễn đồ họa của sự thay đổi tọa độ của một vật theo thời gian trong chuyển động thẳng đều. Đồ thị này giúp ta dễ dàng quan sát và phân tích mối quan hệ giữa vị trí và thời gian.
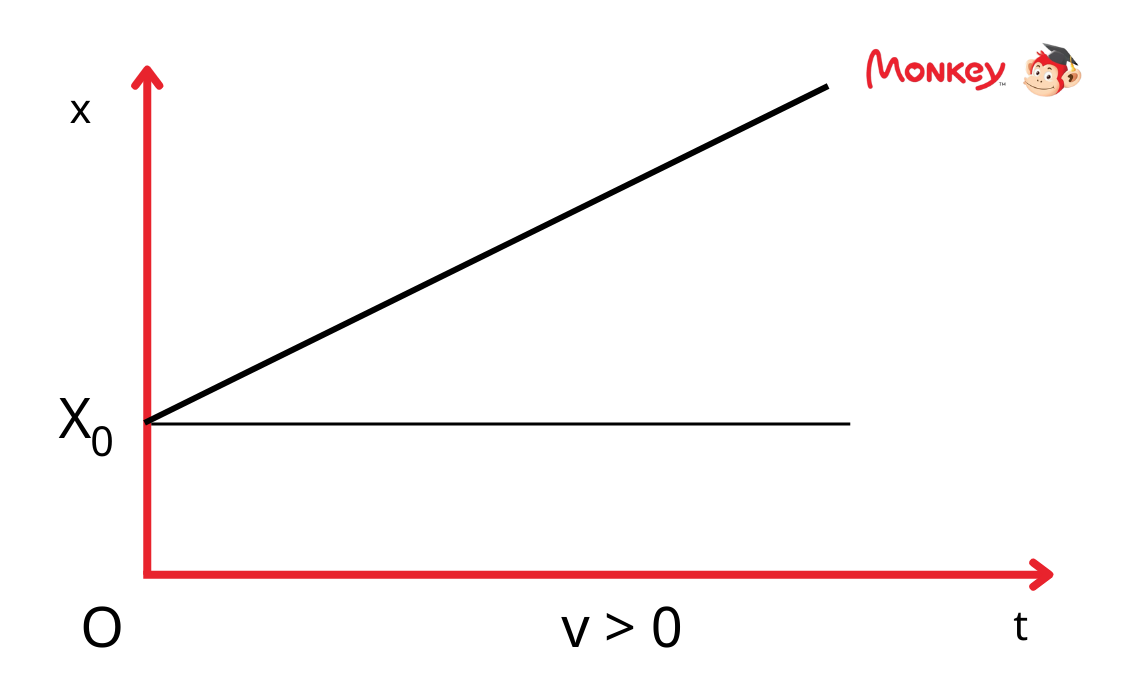
Đối với chuyển động thẳng đều, đồ thị tọa độ - thời gian là một đường thẳng có độ dốc không đổi, biểu diễn vận tốc không đổi của vật. Phương trình của đồ thị có dạng:
\[
x = x_0 + v \cdot t
\]
Trong đó:
- \(x\): Tọa độ của vật tại thời điểm \(t\).
- \(x_0\): Tọa độ ban đầu của vật.
- \(v\): Vận tốc của vật (độ dốc của đồ thị).
- \(t\): Thời gian.
Để vẽ đồ thị tọa độ - thời gian, ta làm theo các bước sau:
- Viết phương trình chuyển động của vật. Ví dụ: \(x = 5 + 10t\), trong đó vận tốc \(v = 10 \, \text{m/s}\) và tọa độ ban đầu \(x_0 = 5 \, \text{m}\).
- Lập bảng giá trị cho các thời điểm khác nhau của \(t\), tính toán tương ứng các giá trị của \(x\).
- Vẽ các điểm tọa độ \(x(t)\) lên hệ trục tọa độ với trục hoành là \(t\) và trục tung là \(x\).
- Nối các điểm bằng một đường thẳng, đây chính là đồ thị của chuyển động thẳng đều.
Ví dụ, với phương trình \(x = 5 + 10t\), bảng giá trị có thể như sau:
| Thời gian (t) | Tọa độ (x) |
| 0 | 5 |
| 1 | 15 |
| 2 | 25 |
| 3 | 35 |
Nhìn vào đồ thị, nếu vận tốc \(v > 0\), đường thẳng sẽ hướng lên, thể hiện sự gia tăng tọa độ theo thời gian. Nếu \(v < 0\), đường thẳng sẽ hướng xuống, thể hiện sự giảm tọa độ theo thời gian.

IV. Đồ thị vận tốc - thời gian
Đồ thị vận tốc - thời gian của chuyển động thẳng đều thể hiện mối quan hệ giữa vận tốc của vật và thời gian. Đối với chuyển động thẳng đều, vận tốc không thay đổi, do đó đồ thị sẽ là một đường thẳng song song với trục thời gian.
Phương trình biểu diễn mối quan hệ vận tốc - thời gian là:
\[
v = \text{hằng số}
\]
Trong đó:
- \(v\): Vận tốc của vật trong suốt quá trình chuyển động.
- \(t\): Thời gian.
Đặc điểm của đồ thị vận tốc - thời gian cho chuyển động thẳng đều:
- Đồ thị là một đường thẳng nằm ngang, vì vận tốc không thay đổi theo thời gian.
- Nếu vật chuyển động theo chiều dương của trục tọa độ, đường thẳng nằm phía trên trục hoành (vận tốc dương).
- Nếu vật chuyển động theo chiều âm của trục tọa độ, đường thẳng nằm phía dưới trục hoành (vận tốc âm).
Ví dụ, nếu một vật có vận tốc không đổi là \(10 \, \text{m/s}\), đồ thị vận tốc - thời gian sẽ có dạng:
| Thời gian (t) | Vận tốc (v) |
| 0 | 10 |
| 1 | 10 |
| 2 | 10 |
| 3 | 10 |
Do vận tốc không thay đổi, mọi giá trị của \(v\) tại các thời điểm khác nhau đều giống nhau, tạo thành đường thẳng ngang trên đồ thị.

V. Bài tập thực hành và ứng dụng
Để hiểu rõ hơn về chuyển động thẳng đều và quỹ đạo của nó, chúng ta sẽ thực hành qua các bài tập sau và khám phá những ứng dụng thực tiễn trong đời sống hằng ngày.
Bài tập thực hành
-
Một xe ô tô chuyển động thẳng đều với vận tốc \( v = 15 \, \text{m/s} \). Tính quãng đường mà xe đã đi được sau 10 giây.
Lời giải:
Sử dụng công thức:
\[
s = v \cdot t
\]
Ta có:
\[
s = 15 \, \text{m/s} \times 10 \, \text{s} = 150 \, \text{m}
\]
Vậy quãng đường xe đã đi được là 150 mét. -
Một người đi bộ với vận tốc không đổi là \( 1.2 \, \text{m/s} \). Sau 5 phút, người đó đã đi được quãng đường bao nhiêu?
Lời giải:
Trước tiên, chuyển đổi thời gian sang đơn vị giây:
\[
t = 5 \, \text{phút} = 5 \times 60 = 300 \, \text{s}
\]
Sử dụng công thức:
\[
s = v \cdot t
\]
Ta có:
\[
s = 1.2 \, \text{m/s} \times 300 \, \text{s} = 360 \, \text{m}
\]
Vậy người đó đã đi được 360 mét. -
Một đoàn tàu chạy với vận tốc \( 20 \, \text{m/s} \) trên quãng đường 500 m. Hỏi thời gian để tàu đi hết quãng đường này là bao nhiêu?
Lời giải:
Sử dụng công thức:
\[
t = \frac{s}{v}
\]
Ta có:
\[
t = \frac{500 \, \text{m}}{20 \, \text{m/s}} = 25 \, \text{giây}
\]
Vậy thời gian để tàu đi hết quãng đường là 25 giây.
Ứng dụng trong đời sống
- Chuyển động thẳng đều thường thấy trong hệ thống băng tải của các nhà máy sản xuất, nơi các vật thể di chuyển với vận tốc không đổi trên quỹ đạo thẳng.
- Các phương tiện giao thông như tàu điện, xe bus di chuyển trên đường thẳng với vận tốc ổn định cũng là ví dụ về chuyển động thẳng đều.
- Trong lĩnh vực hàng không, khi máy bay duy trì vận tốc không đổi trong các giai đoạn bay bằng, nó cũng tuân theo quy luật của chuyển động thẳng đều.