PT Giao Thoa Sóng: Hiểu Rõ Hiện Tượng Và Ứng Dụng Trong Cuộc Sống

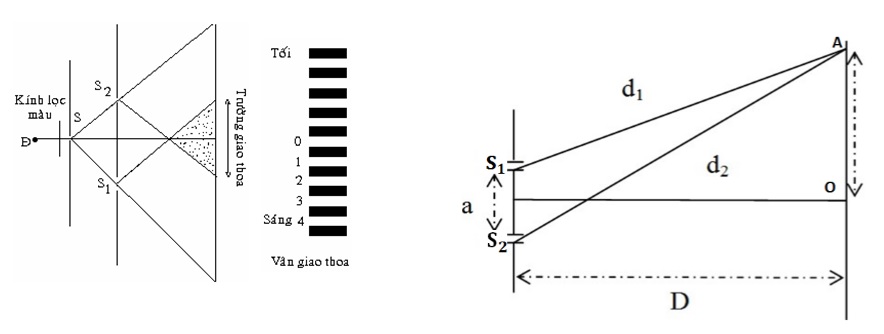
Giao thoa sóng là hiện tượng khi hai sóng gặp nhau và tạo ra các điểm mà biên độ sóng tăng cường hoặc giảm bớt. Hiện tượng này xảy ra khi hai nguồn sóng kết hợp, có cùng tần số và có hiệu số pha không đổi theo thời gian. Hiện tượng giao thoa sóng có thể được quan sát trong các thí nghiệm về sóng cơ và sóng ánh sáng.

Điều kiện để có giao thoa sóng

• Hai nguồn sóng phải là hai nguồn kết hợp, nghĩa là chúng phải có cùng tần số và hiệu số pha không đổi.
• Các sóng phải có cùng biên độ hoặc biên độ gần bằng nhau.

Phương trình giao thoa sóng

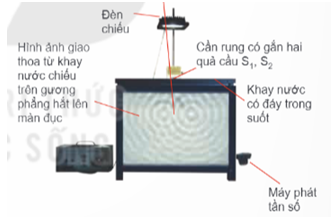
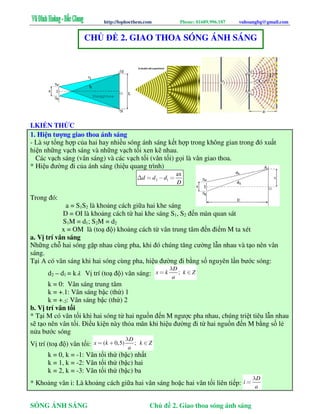
Xét hai nguồn sóng kết hợp \(S_1\) và \(S_2\), phương trình sóng tại một điểm \(M\) trên mặt nước có thể biểu diễn như sau:

• Phương trình sóng tại hai nguồn:

\[ u_1 = A\cos(2\pi ft + \varphi_1) \]

\[ u_2 = A\cos(2\pi ft + \varphi_2) \]

• Phương trình sóng tổng hợp tại điểm M:

\[ u_M = u_{1M} + u_{2M} = 2A \cos\left(\pi \frac{d_2 - d_1}{\lambda}\right) \cos\left(2\pi ft - \pi \frac{d_1 + d_2}{\lambda} + \frac{\varphi_1 + \varphi_2}{2}\right) \]

• Biên độ sóng tại điểm M:

\[ A_M = 2A \left|\cos\left(\pi \frac{d_2 - d_1}{\lambda}\right)\right| \]

Các điểm cực đại và cực tiểu trong giao thoa sóng

Các điểm cực đại là các điểm mà hai sóng thành phần dao động cùng pha, và biên độ tổng hợp tại đó là lớn nhất. Ngược lại, các điểm cực tiểu là các điểm mà hai sóng dao động ngược pha, và biên độ tổng hợp tại đó bằng không.

Công thức tính vị trí các điểm cực đại, cực tiểu

• Điểm cực đại:

\[ d_2 - d_1 = k\lambda \] (với \(k \in \mathbb{Z}\))

• Điểm cực tiểu:

\[ d_2 - d_1 = \left(k + \frac{1}{2}\right)\lambda \] (với \(k \in \mathbb{Z}\))

Ứng dụng của giao thoa sóng

• Trong nghiên cứu vật lý, giao thoa sóng giúp xác định bước sóng của sóng và tính chất của các nguồn sóng.
• Trong công nghệ, hiện tượng này được ứng dụng trong thiết kế các thiết bị giao thoa, như máy quang phổ và các hệ thống truyền thông.

Giao thoa sóng là một hiện tượng quan trọng trong vật lý, xảy ra khi hai hoặc nhiều sóng gặp nhau và kết hợp, tạo ra các vùng mà biên độ sóng tăng cường hoặc giảm bớt. Hiện tượng này được quan sát rõ nhất trong sóng cơ học và sóng ánh sáng, với những ứng dụng quan trọng trong nhiều lĩnh vực khác nhau.

• Định nghĩa: Giao thoa sóng là quá trình chồng chập của hai hay nhiều sóng từ các nguồn kết hợp, làm thay đổi biên độ sóng tại các điểm giao thoa.
• Các loại giao thoa:
  • Giao thoa sóng cơ: Xảy ra khi hai sóng cơ gặp nhau, chẳng hạn như sóng trên mặt nước hoặc sóng âm thanh.
  • Giao thoa sóng ánh sáng: Xảy ra khi hai sóng ánh sáng kết hợp, gây ra hiện tượng sáng tối xen kẽ.
• Điều kiện giao thoa:
  • Hai nguồn sóng phải là nguồn kết hợp, có cùng tần số và hiệu số pha không đổi.
  • Các sóng phải truyền trong cùng một môi trường và có cùng tốc độ.
• Ứng dụng: Hiện tượng giao thoa sóng được ứng dụng trong nhiều lĩnh vực như:
  • Quang học: Thiết kế các thiết bị quang học như máy quang phổ, hệ thống giao thoa kế.
  • Công nghệ: Phát triển các thiết bị truyền thông, đo lường chính xác.
  • Vật lý hạt nhân: Nghiên cứu cấu trúc hạt nhân và sóng điện từ.

Giao thoa sóng không chỉ là một hiện tượng tự nhiên mà còn là một công cụ mạnh mẽ trong nghiên cứu và ứng dụng công nghệ. Việc hiểu rõ và nắm vững các nguyên lý của giao thoa sóng sẽ giúp chúng ta khai thác tối đa tiềm năng của hiện tượng này trong cuộc sống hàng ngày và trong các lĩnh vực khoa học, công nghệ.

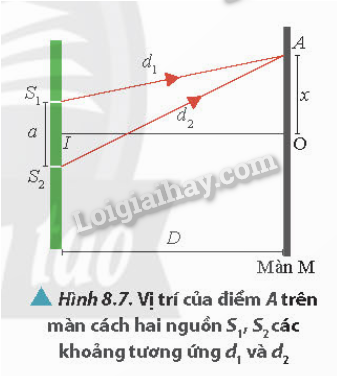
Giao thoa sóng xảy ra khi hai hay nhiều sóng gặp nhau và tạo ra hiện tượng chồng chất, gây ra các điểm có biên độ sóng cực đại hoặc cực tiểu. Để hiện tượng giao thoa xảy ra, cần phải thỏa mãn một số điều kiện cụ thể, giúp xác định các đặc điểm của sóng và vị trí giao thoa.

• 1. Hai nguồn sóng kết hợp:

  Hai nguồn sóng phải là hai nguồn kết hợp, nghĩa là chúng có cùng tần số và hiệu số pha không đổi theo thời gian. Khi hai nguồn có cùng tần số và pha không đổi, các sóng từ hai nguồn sẽ dao động đồng bộ và tạo ra các vân giao thoa ổn định.

• 2. Sóng truyền trong cùng một môi trường:

  Để giao thoa xảy ra, các sóng phải truyền trong cùng một môi trường đồng nhất. Nếu môi trường thay đổi, tốc độ và đặc tính của sóng cũng thay đổi, dẫn đến hiện tượng giao thoa không rõ ràng hoặc bị biến dạng.

• 3. Sóng có cùng biên độ hoặc gần bằng nhau:

  Biên độ của các sóng tham gia giao thoa cần phải bằng nhau hoặc gần bằng nhau để tạo ra các vân giao thoa rõ ràng. Nếu biên độ khác nhau quá lớn, hiện tượng giao thoa có thể bị mờ hoặc không xảy ra rõ ràng.

• 4. Điều kiện về vị trí và khoảng cách:

  Khoảng cách giữa hai nguồn sóng và vị trí quan sát cũng là một yếu tố quan trọng. Khoảng cách này phải đủ nhỏ để các sóng có thể chồng chất và tạo ra các điểm cực đại và cực tiểu rõ ràng.

Khi các điều kiện trên được thỏa mãn, hiện tượng giao thoa sẽ xảy ra một cách rõ ràng và dễ quan sát. Các vân giao thoa sẽ xuất hiện, với các điểm cực đại tại những nơi hai sóng kết hợp đồng pha, và các điểm cực tiểu tại những nơi hai sóng ngược pha.

Phương trình giao thoa sóng mô tả sự tổng hợp của hai hay nhiều sóng tại một điểm trong không gian. Khi hai sóng có cùng tần số và biên độ gặp nhau, chúng sẽ chồng chập và tạo ra các vân giao thoa. Phương trình này giúp xác định biên độ dao động tổng hợp tại mỗi điểm cũng như vị trí của các cực đại và cực tiểu giao thoa.

• 1. Phương trình sóng tại hai nguồn:

  Xét hai nguồn sóng kết hợp \(S_1\) và \(S_2\), phương trình sóng tại mỗi nguồn có thể biểu diễn như sau:

  \[ u_1 = A \cos(2\pi ft + \varphi_1) \]

  \[ u_2 = A \cos(2\pi ft + \varphi_2) \]

• 2. Phương trình sóng tổng hợp tại một điểm:

  Tại một điểm \(M\) trong không gian, phương trình của sóng tổng hợp là tổng của hai sóng đến từ \(S_1\) và \(S_2\):

  \[ u_M = u_{1M} + u_{2M} = A \cos(2\pi ft + \varphi_1) + A \cos(2\pi ft + \varphi_2) \]

  Sử dụng công thức cộng sóng, phương trình trên có thể được viết lại như:

  \[ u_M = 2A \cos\left(\frac{\varphi_1 + \varphi_2}{2}\right) \cos\left(2\pi ft + \frac{\varphi_1 - \varphi_2}{2}\right) \]

• 3. Biên độ sóng tổng hợp:

  Biên độ của sóng tổng hợp tại điểm \(M\) được xác định bởi:

  \[ A_M = 2A \left|\cos\left(\frac{\varphi_1 - \varphi_2}{2}\right)\right| \]

  Biên độ này phụ thuộc vào hiệu số pha của hai sóng tại vị trí điểm \(M\).

• 4. Điều kiện giao thoa cực đại và cực tiểu:

  Hiện tượng giao thoa cực đại xảy ra khi hiệu số pha giữa hai sóng là bội số nguyên của \(2\pi\):

  \[ \varphi_1 - \varphi_2 = 2k\pi \quad (k \in \mathbb{Z}) \]

  Hiện tượng giao thoa cực tiểu xảy ra khi hiệu số pha giữa hai sóng là bội số lẻ của \(\pi\):

  \[ \varphi_1 - \varphi_2 = (2k + 1)\pi \quad (k \in \mathbb{Z}) \]

Phương trình giao thoa sóng không chỉ giúp xác định vị trí các điểm giao thoa cực đại và cực tiểu mà còn cho thấy sự biến đổi biên độ dao động theo từng điểm trong không gian. Việc hiểu rõ phương trình này rất quan trọng trong việc nghiên cứu các hiện tượng sóng và ứng dụng của chúng trong các lĩnh vực như quang học, âm học, và công nghệ truyền thông.

Dưới đây là một số dạng bài tập về giao thoa sóng, bao gồm cả bài tập cơ bản và nâng cao, giúp học sinh nắm vững kiến thức và ứng dụng phương trình giao thoa sóng trong các bài toán thực tế. Mỗi bài tập đều có lời giải chi tiết, hỗ trợ người học từng bước để hiểu rõ hơn về hiện tượng giao thoa sóng.

1. Dạng 1: Xác định vị trí các điểm cực đại và cực tiểu giao thoa

   Cho hai nguồn sóng kết hợp \(S_1\) và \(S_2\) phát ra hai sóng cùng tần số và cùng pha. Hãy xác định vị trí các điểm cực đại và cực tiểu giao thoa trên đoạn thẳng nối hai nguồn.

   Lời giải: Sử dụng phương trình hiệu số pha và điều kiện giao thoa cực đại, cực tiểu để xác định.

2. Dạng 2: Tính khoảng cách giữa hai vân giao thoa cực đại liên tiếp

   Hai nguồn sóng \(S_1\) và \(S_2\) phát ra sóng với bước sóng \(\lambda\). Hãy tính khoảng cách giữa hai vân cực đại liên tiếp trên màn giao thoa.

   Lời giải: Khoảng cách này được tính bằng công thức \(\Delta x = \frac{\lambda D}{a}\), trong đó \(D\) là khoảng cách từ hai nguồn đến màn, \(a\) là khoảng cách giữa hai nguồn.

3. Dạng 3: Tìm số vân cực đại và cực tiểu trên đoạn thẳng giữa hai nguồn

   Với hai nguồn sóng có khoảng cách \(d\) và phát ra sóng có bước sóng \(\lambda\), hãy tính số vân cực đại và cực tiểu xuất hiện trên đoạn thẳng nối hai nguồn.

   Lời giải: Sử dụng điều kiện giao thoa để đếm số vân trên đoạn thẳng.

4. Dạng 4: Xác định pha ban đầu của sóng tại một điểm

   Tại điểm \(M\) trên màn giao thoa, sóng từ \(S_1\) và \(S_2\) có pha ban đầu khác nhau. Hãy tính pha ban đầu tại \(M\).

   Lời giải: Sử dụng phương trình sóng và hiệu số pha để tìm pha ban đầu tại điểm \(M\).

5. Dạng 5: Bài toán ngược: Tìm vị trí nguồn sóng từ các vân giao thoa

   Cho biết các vân giao thoa trên màn và khoảng cách giữa chúng. Hãy tìm vị trí và khoảng cách giữa các nguồn sóng.

   Lời giải: Sử dụng dữ liệu từ các vân để giải bài toán ngược và tìm vị trí của các nguồn.

6. Dạng 6: Tính tần số sóng từ các vân giao thoa

   Biết khoảng cách giữa các vân cực đại và khoảng cách từ hai nguồn đến màn, hãy tính tần số của sóng phát ra từ hai nguồn.

   Lời giải: Sử dụng công thức liên quan đến tần số và bước sóng để tính tần số.

7. Dạng 7: Xác định biên độ tổng hợp tại một điểm

   Cho hai sóng có biên độ \(A_1\) và \(A_2\) gặp nhau tại một điểm \(M\). Hãy xác định biên độ tổng hợp tại \(M\).

   Lời giải: Sử dụng công thức cộng sóng để xác định biên độ tổng hợp.

8. Dạng 8: Xác định thời gian xuất hiện giao thoa cực đại đầu tiên

   Sóng từ hai nguồn phát ra cùng lúc, hãy tính thời gian để vân cực đại đầu tiên xuất hiện tại một điểm trên màn.

   Lời giải: Sử dụng điều kiện giao thoa và tính toán thời gian dựa trên tốc độ sóng.

9. Dạng 9: Tính cường độ sáng tại các vân giao thoa

   Cường độ sáng tại các vân giao thoa phụ thuộc vào biên độ sóng. Hãy tính cường độ sáng tại một vân cực đại và một vân cực tiểu.

   Lời giải: Sử dụng công thức cường độ sáng \(I \propto A^2\) để tính toán.

10. Dạng 10: Xác định bước sóng từ các vân giao thoa

    Dựa trên khoảng cách giữa các vân giao thoa trên màn, hãy xác định bước sóng của sóng phát ra từ hai nguồn.

    Lời giải: Sử dụng công thức liên quan giữa khoảng cách vân và bước sóng để tính bước sóng.