Chủ đề giao thoa kế michelson: Giao thoa kế Michelson là một trong những phát minh quan trọng nhất trong lĩnh vực quang học, đóng vai trò chủ chốt trong nhiều thí nghiệm khoa học và ứng dụng công nghệ. Bài viết này sẽ giúp bạn khám phá nguyên lý hoạt động, các ứng dụng thực tiễn và tầm quan trọng của giao thoa kế Michelson trong nghiên cứu và công nghiệp hiện đại.
Mục lục
- Giao Thoa Kế Michelson: Nguyên Lý Hoạt Động và Ứng Dụng
- 1. Giới Thiệu Về Giao Thoa Kế Michelson
- 2. Ứng Dụng Của Giao Thoa Kế Michelson Trong Thực Tế
- 3. Phân Loại Giao Thoa Kế
- 4. Các Thí Nghiệm Sử Dụng Giao Thoa Kế Michelson
- 5. Bài Tập và Giải Bài Tập Về Giao Thoa Kế Michelson
- Bài Tập 1: Tính toán bước sóng ánh sáng từ dữ liệu giao thoa
- Bài Tập 2: Phân tích kết quả thí nghiệm Michelson-Morley
- Bài Tập 3: Đo độ dịch chuyển nhỏ trong hệ thống quang học
- Bài Tập 4: So sánh giao thoa kế Michelson và Fabry-Perot
- Bài Tập 5: Tính toán độ phân giải của giao thoa kế Michelson
- Bài Tập 6: Ứng dụng giao thoa kế Michelson trong đo sóng hấp dẫn
- Bài Tập 7: Phân tích ảnh hưởng của góc tới và góc phản xạ trong giao thoa kế Michelson
- Bài Tập 8: Tính toán quang lộ trong giao thoa kế Michelson
- Bài Tập 9: Đánh giá sai số trong phép đo bằng giao thoa kế Michelson
- Bài Tập 10: Thiết kế một thí nghiệm sử dụng giao thoa kế Michelson để đo tốc độ ánh sáng
Giao Thoa Kế Michelson: Nguyên Lý Hoạt Động và Ứng Dụng
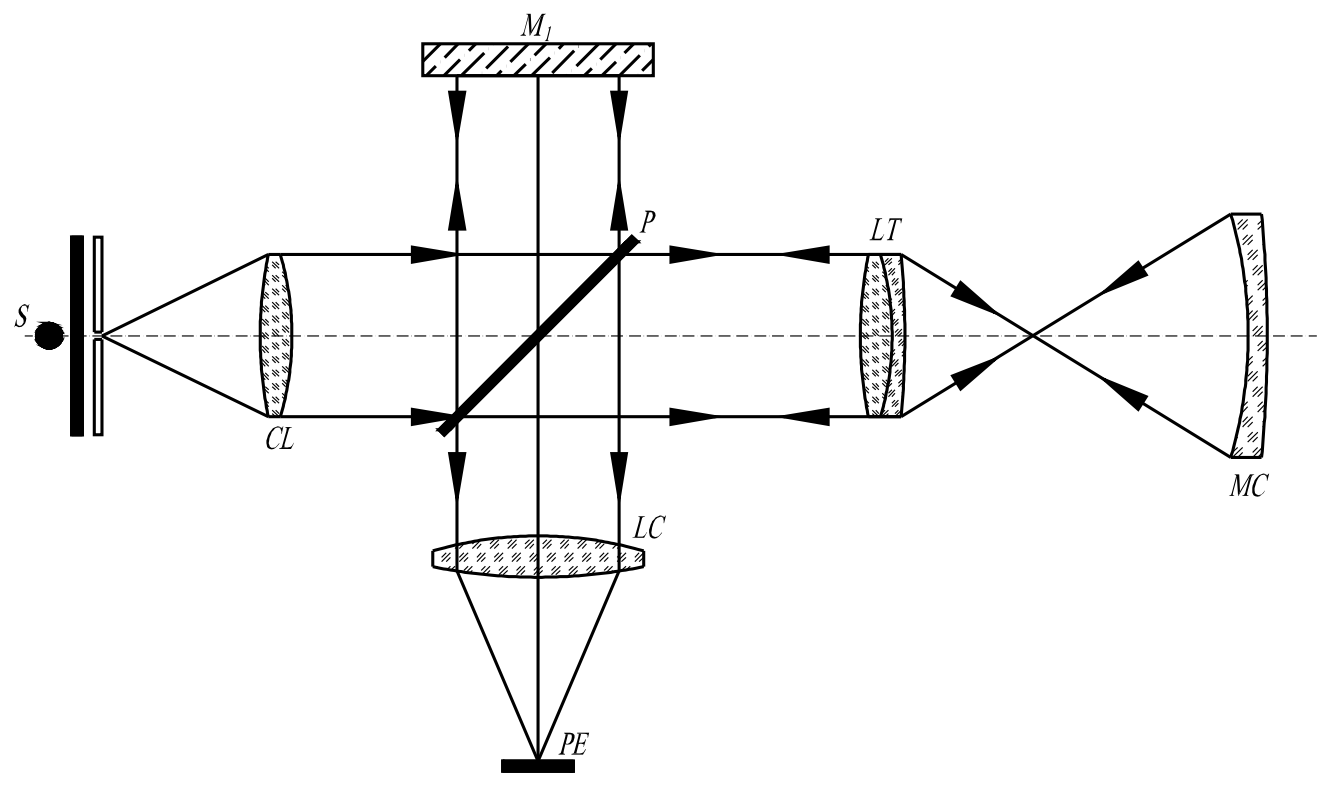
Giao thoa kế Michelson là một thiết bị quang học được phát minh bởi Albert A. Michelson vào cuối thế kỷ 19. Nó đóng vai trò quan trọng trong nhiều thí nghiệm vật lý và ứng dụng công nghiệp. Dưới đây là những thông tin chi tiết về nguyên lý hoạt động, ứng dụng và các khía cạnh kỹ thuật liên quan.
Nguyên Lý Hoạt Động
Giao thoa kế Michelson hoạt động dựa trên nguyên lý giao thoa ánh sáng. Thiết bị này sử dụng một nguồn sáng (thường là laser), chia chùm tia sáng thành hai phần bằng một gương bán mạ. Hai chùm tia này sau đó phản xạ từ hai gương khác nhau và được ghép lại với nhau. Khi hai chùm tia này gặp nhau, chúng tạo ra các vân giao thoa, từ đó có thể tính toán được sự thay đổi khoảng cách rất nhỏ.
Phương Trình Giao Thoa
Hiện tượng giao thoa có thể được mô tả bằng phương trình:
\[
I = I_0 \left[ 1 + \cos\left(\frac{2\pi \Delta d}{\lambda}\right) \right]
\]
Trong đó:
- \(I\) là cường độ sáng tại điểm giao thoa.
- \(I_0\) là cường độ sáng ban đầu.
- \(\Delta d\) là sự chênh lệch quang lộ giữa hai chùm sáng.
- \(\lambda\) là bước sóng của ánh sáng sử dụng.
Ứng Dụng Trong Khoa Học và Công Nghiệp
- Đo Đạc Chính Xác: Giao thoa kế Michelson được sử dụng để đo khoảng cách và các thay đổi rất nhỏ với độ chính xác cao, đặc biệt trong ngành công nghiệp hàng không, không gian.
- Thí Nghiệm Vật Lý: Nó được sử dụng trong nhiều thí nghiệm vật lý cơ bản như xác định tốc độ ánh sáng và nghiên cứu về sóng ánh sáng.
- Ứng Dụng Trong Quang Học: Giao thoa kế Michelson được sử dụng trong sản xuất các thiết bị quang học như laser, cảm biến quang học và trong công nghiệp viễn thám.
Giao Thoa Kế Michelson và Lý Thuyết Sóng Ánh Sáng
Giao thoa kế Michelson cũng đóng vai trò quan trọng trong việc kiểm chứng các lý thuyết về ánh sáng, như thuyết sóng của ánh sáng. Bằng cách thay đổi các điều kiện thí nghiệm (ví dụ như thay đổi nguồn sáng hoặc sử dụng các loại gương khác nhau), các nhà khoa học có thể quan sát và kiểm tra các hiện tượng giao thoa khác nhau.
Lợi Ích và Ứng Dụng Thực Tiễn
Giao thoa kế Michelson không chỉ là một công cụ nghiên cứu mà còn có các ứng dụng thực tiễn trong các lĩnh vực khác nhau, từ nghiên cứu vật lý cơ bản đến các ứng dụng trong y tế và công nghiệp, như việc đo đạc trong sản xuất các thiết bị quang học hiện đại.
| Ứng Dụng | Chi Tiết |
| Đo lường chính xác | Ứng dụng trong các ngành công nghiệp yêu cầu độ chính xác cao như hàng không, không gian. |
| Thí nghiệm vật lý | Kiểm tra các lý thuyết vật lý cơ bản và nghiên cứu sóng ánh sáng. |
| Sản xuất thiết bị quang học | Ứng dụng trong công nghiệp quang học để sản xuất các thiết bị như laser và cảm biến quang học. |
Với những tính năng và ứng dụng đa dạng, giao thoa kế Michelson là một công cụ không thể thiếu trong nghiên cứu khoa học và công nghệ hiện đại.

.png)
1. Giới Thiệu Về Giao Thoa Kế Michelson
Giao thoa kế Michelson là một thiết bị quang học được phát minh bởi nhà vật lý người Mỹ Albert A. Michelson vào cuối thế kỷ 19. Thiết bị này được thiết kế để đo lường các khoảng cách rất nhỏ và các thay đổi trong quang lộ, dựa trên hiện tượng giao thoa ánh sáng.
Giao thoa kế Michelson hoạt động dựa trên nguyên lý chia chùm tia sáng thành hai phần bằng một gương bán mạ. Hai chùm tia này sau đó phản xạ từ hai gương khác nhau và được ghép lại. Khi các chùm tia gặp nhau, chúng tạo ra các vân giao thoa, cho phép tính toán sự thay đổi khoảng cách rất nhỏ.
Thiết bị này có cấu trúc cơ bản gồm ba thành phần chính:
- Nguồn sáng: Thường sử dụng nguồn sáng đơn sắc, chẳng hạn như laser.
- Gương bán mạ: Dùng để chia chùm sáng ban đầu thành hai phần.
- Gương phản xạ: Hai gương đặt ở hai vị trí khác nhau để phản xạ lại các chùm tia sáng.
Giao thoa kế Michelson đã góp phần quan trọng vào các thí nghiệm nổi tiếng như thí nghiệm Michelson-Morley, nhằm kiểm tra giả thuyết về sự tồn tại của ête - một môi trường giả định mà người ta từng cho rằng ánh sáng truyền qua. Kết quả của thí nghiệm này đã mở đường cho sự phát triển của thuyết tương đối đặc biệt của Albert Einstein.
Ngày nay, giao thoa kế Michelson không chỉ được sử dụng trong nghiên cứu khoa học mà còn có ứng dụng rộng rãi trong công nghiệp, đặc biệt là trong đo lường chính xác và quang học.
2. Ứng Dụng Của Giao Thoa Kế Michelson Trong Thực Tế
Giao thoa kế Michelson là một công cụ quan trọng trong nhiều lĩnh vực khoa học và công nghệ, nhờ khả năng đo lường chính xác các khoảng cách và thay đổi nhỏ. Dưới đây là một số ứng dụng thực tiễn nổi bật của giao thoa kế Michelson:
- 1. Đo lường chính xác trong công nghiệp: Giao thoa kế Michelson được sử dụng để đo các khoảng cách cực nhỏ với độ chính xác cao trong sản xuất và kiểm tra chất lượng. Ví dụ, trong công nghiệp sản xuất bán dẫn, nó giúp đo độ dày của các lớp vật liệu trên bề mặt chip.
- 2. Ứng dụng trong quang học: Trong ngành quang học, giao thoa kế Michelson được sử dụng để kiểm tra các đặc tính của thấu kính, gương, và các thiết bị quang học khác. Thiết bị này giúp xác định độ phẳng, độ cong, và các khuyết tật của bề mặt quang học.
- 3. Thí nghiệm Michelson-Morley: Một trong những ứng dụng nổi tiếng nhất của giao thoa kế Michelson là trong thí nghiệm Michelson-Morley, nhằm kiểm tra sự tồn tại của ête, một giả thuyết về môi trường truyền sóng ánh sáng. Kết quả của thí nghiệm này đã dẫn đến sự phát triển của thuyết tương đối đặc biệt của Einstein.
- 4. Đo sóng hấp dẫn: Trong vật lý thiên văn, giao thoa kế Michelson được sử dụng trong các máy dò sóng hấp dẫn như LIGO (Laser Interferometer Gravitational-Wave Observatory). Thiết bị này giúp phát hiện những dao động rất nhỏ trong không gian thời gian do các sự kiện vũ trụ như va chạm hố đen gây ra.
- 5. Y học và sinh học: Giao thoa kế Michelson cũng được ứng dụng trong y học và sinh học để đo các đặc tính của tế bào và mô. Ví dụ, nó có thể được sử dụng để đo đạc chính xác sự thay đổi kích thước của tế bào trong quá trình nghiên cứu bệnh học.
- 6. Đo sự thay đổi nhiệt độ: Giao thoa kế Michelson còn được sử dụng để đo sự giãn nở nhiệt của vật liệu bằng cách theo dõi sự thay đổi quang lộ của các chùm tia sáng khi nhiệt độ thay đổi.
Với những ứng dụng đa dạng trong nhiều lĩnh vực, giao thoa kế Michelson đã chứng tỏ vai trò quan trọng của nó trong việc thúc đẩy sự phát triển của khoa học và công nghệ hiện đại.

3. Phân Loại Giao Thoa Kế
Giao thoa kế là thiết bị quang học được sử dụng để phân tích sự giao thoa của sóng ánh sáng, giúp đo lường các khoảng cách nhỏ và các thay đổi quang lộ chính xác. Trong thực tế, có nhiều loại giao thoa kế khác nhau được phát triển dựa trên nguyên lý cơ bản của giao thoa, trong đó giao thoa kế Michelson là loại nổi tiếng nhất. Dưới đây là các phân loại chính của giao thoa kế:
- 1. Giao Thoa Kế Michelson: Đây là loại giao thoa kế cổ điển và phổ biến nhất. Nó được sử dụng rộng rãi trong các thí nghiệm vật lý và ứng dụng công nghiệp. Nguyên lý hoạt động dựa trên việc chia chùm tia sáng thành hai phần, phản xạ qua hai gương rồi kết hợp lại để tạo ra vân giao thoa.
- 2. Giao Thoa Kế Fabry-Pérot: Khác với Michelson, giao thoa kế Fabry-Pérot sử dụng hai gương bán mạ song song để tạo ra các phản xạ liên tiếp, dẫn đến sự hình thành các vân giao thoa. Thiết bị này được sử dụng để đo các bước sóng ánh sáng với độ phân giải cao.
- 3. Giao Thoa Kế Twyman-Green: Đây là một biến thể của giao thoa kế Michelson, được thiết kế đặc biệt để kiểm tra và đo đạc các hệ thống quang học như thấu kính và gương. Giao thoa kế Twyman-Green thường được sử dụng trong lĩnh vực chế tạo và kiểm tra chất lượng quang học.
- 4. Giao Thoa Kế Sagnac: Giao thoa kế này dựa trên hiện tượng Sagnac, nơi một chùm sáng được chia thành hai phần di chuyển theo các hướng đối diện trong một vòng kín. Đây là nguyên lý cơ bản của các con quay laser, được sử dụng trong các hệ thống dẫn đường và đo đạc quán tính.
- 5. Giao Thoa Kế Linnik: Một biến thể khác của giao thoa kế Michelson, giao thoa kế Linnik được thiết kế để quan sát các mẫu vật quang học không đồng nhất, cho phép nghiên cứu các bề mặt và cấu trúc vi mô.
- 6. Giao Thoa Kế Mach-Zehnder: Loại giao thoa kế này được sử dụng chủ yếu trong các nghiên cứu về quang học phi tuyến và truyền thông quang học. Nó hoạt động bằng cách chia chùm sáng thành hai phần và cho chúng đi qua các đường quang học khác nhau trước khi tái kết hợp.
Mỗi loại giao thoa kế đều có ưu điểm riêng và được tối ưu hóa cho các ứng dụng cụ thể. Việc chọn lựa loại giao thoa kế phù hợp phụ thuộc vào yêu cầu đo lường và đặc tính của hệ thống cần phân tích.

XEM THÊM:
4. Các Thí Nghiệm Sử Dụng Giao Thoa Kế Michelson
Giao thoa kế Michelson đã được sử dụng trong nhiều thí nghiệm quan trọng trong lịch sử khoa học, giúp xác minh các lý thuyết vật lý và khám phá những hiện tượng mới. Dưới đây là một số thí nghiệm nổi bật sử dụng thiết bị này:
- 1. Thí Nghiệm Michelson-Morley: Đây là một trong những thí nghiệm nổi tiếng nhất trong lịch sử khoa học. Mục đích của thí nghiệm là kiểm tra sự tồn tại của ête, một môi trường giả định mà ánh sáng được cho là truyền qua. Kết quả âm tính của thí nghiệm này đã góp phần vào sự phát triển của thuyết tương đối đặc biệt của Einstein, khẳng định rằng tốc độ ánh sáng không phụ thuộc vào chuyển động của nguồn sáng hoặc người quan sát.
- 2. Thí Nghiệm Xác Định Bước Sóng Ánh Sáng: Giao thoa kế Michelson được sử dụng để xác định chính xác bước sóng của các nguồn sáng đơn sắc. Bằng cách tạo ra vân giao thoa và đo lường khoảng cách giữa các vân, các nhà khoa học có thể tính toán bước sóng của ánh sáng với độ chính xác rất cao.
- 3. Thí Nghiệm Đo Sự Giãn Nở Nhiệt: Thiết bị này cũng được sử dụng để đo sự giãn nở nhiệt của vật liệu. Khi một vật liệu được nung nóng, nó sẽ giãn nở, dẫn đến sự thay đổi quang lộ của chùm sáng trong giao thoa kế. Bằng cách đo sự dịch chuyển của các vân giao thoa, người ta có thể xác định mức độ giãn nở của vật liệu.
- 4. Thí Nghiệm Đo Sự Chênh Lệch Chiết Suất: Giao thoa kế Michelson có thể được sử dụng để đo sự chênh lệch chiết suất giữa hai môi trường. Khi một chùm sáng đi qua hai môi trường khác nhau, sự khác biệt về chiết suất sẽ làm dịch chuyển vị trí của các vân giao thoa, cho phép tính toán chính xác sự chênh lệch chiết suất.
- 5. Thí Nghiệm Trong Vật Lý Thiên Văn: Trong vật lý thiên văn, giao thoa kế Michelson đã được sử dụng để đo các hiện tượng vũ trụ, như sự giãn nở của các thiên hà và đo sóng hấp dẫn trong các thí nghiệm như LIGO. Những ứng dụng này đã mang lại những hiểu biết quan trọng về cấu trúc và sự tiến hóa của vũ trụ.
Những thí nghiệm trên chỉ là một phần nhỏ trong các ứng dụng của giao thoa kế Michelson. Thiết bị này tiếp tục đóng vai trò quan trọng trong nhiều nghiên cứu khoa học hiện đại, chứng minh tính ứng dụng rộng rãi và giá trị của nó trong việc khám phá thế giới tự nhiên.

5. Bài Tập và Giải Bài Tập Về Giao Thoa Kế Michelson
Dưới đây là một số bài tập liên quan đến giao thoa kế Michelson, kèm theo các bước giải chi tiết giúp bạn nắm vững cách sử dụng thiết bị này trong các tình huống thực tế.
- Bài tập 1: Tính toán bước sóng ánh sáng
Cho một giao thoa kế Michelson với độ dài hai cánh tay lần lượt là \(L_1\) và \(L_2\). Khi thay đổi độ dài một cánh tay thêm một khoảng \(\Delta L\), số vân sáng di chuyển là \(N\). Hãy tính bước sóng \(\lambda\) của ánh sáng sử dụng giao thoa kế.
Giải:
-
Bước 1: Xác định sự thay đổi quang lộ \(\Delta L\) bằng cách sử dụng công thức:
\[ \Delta L = N \cdot \lambda \] -
Bước 2: Từ đó, bước sóng \(\lambda\) của ánh sáng được tính bằng:
\[ \lambda = \frac{\Delta L}{N} \] -
Ví dụ: Nếu \(N = 100\) và \(\Delta L = 0.05\) mm, ta có:
\[ \lambda = \frac{0.05 \text{ mm}}{100} = 500 \text{ nm} \]
- Bài tập 2: Xác định sự dịch chuyển của vân giao thoa
Trong một thí nghiệm, một trong hai gương của giao thoa kế Michelson được dịch chuyển một khoảng \(d = 1\) µm. Tính số vân sáng di chuyển trên màn hình.
Giải:
-
Bước 1: Công thức tính số vân sáng di chuyển:
\[ N = \frac{2d}{\lambda} \] -
Bước 2: Với \(\lambda = 500\) nm, ta có:
\[ N = \frac{2 \cdot 1 \text{ µm}}{500 \text{ nm}} = 4 \text{ vân} \]
- Bài tập 3: Ứng dụng trong đo chiết suất của không khí
Sử dụng giao thoa kế Michelson để đo chiết suất của không khí. Khi một ống kính dài \(L = 10\) cm được đặt trong một cánh tay của giao thoa kế và áp suất không khí trong ống thay đổi, số vân sáng di chuyển là \(N = 200\). Tính chiết suất của không khí.
Giải:
-
Bước 1: Công thức liên hệ giữa chiết suất và số vân sáng:
\[ N = \frac{2L(n-1)}{\lambda} \] -
Bước 2: Với \(L = 10\) cm, \(\lambda = 500\) nm và \(N = 200\), ta tính được:
\[ n = 1 + \frac{N \cdot \lambda}{2L} = 1 + \frac{200 \cdot 500 \text{ nm}}{2 \cdot 10 \text{ cm}} \approx 1.0001 \]
Trên đây là các bài tập tiêu biểu về giao thoa kế Michelson, giúp củng cố kiến thức lý thuyết và nâng cao khả năng ứng dụng thực tế của thiết bị này trong các lĩnh vực khoa học.
Bài Tập 1: Tính toán bước sóng ánh sáng từ dữ liệu giao thoa
Bài tập này yêu cầu bạn sử dụng dữ liệu thu được từ thí nghiệm giao thoa sử dụng giao thoa kế Michelson để tính toán bước sóng của ánh sáng được sử dụng. Chúng ta sẽ làm việc theo từng bước để đảm bảo rằng bạn có thể áp dụng phương pháp này vào thực tế một cách hiệu quả.
-
Bước 1: Xác định số vân giao thoa \(N\)
Khi một trong hai gương của giao thoa kế Michelson được dịch chuyển một khoảng \(\Delta d\), số vân sáng hoặc tối di chuyển qua màn sẽ được đếm và ký hiệu là \(N\). Hãy ghi lại số vân \(N\) mà bạn quan sát được.
-
Bước 2: Đo khoảng cách dịch chuyển của gương \(\Delta d\)
Dùng một dụng cụ đo chính xác để xác định khoảng cách \(\Delta d\) mà gương đã dịch chuyển trong thí nghiệm. Đơn vị thường dùng là milimet (mm).
-
Bước 3: Áp dụng công thức tính bước sóng
Bước sóng ánh sáng \(\lambda\) được tính bằng công thức:
\[ \lambda = \frac{2\Delta d}{N} \]Trong đó:
- \(\Delta d\) là khoảng cách dịch chuyển của gương
- \(N\) là số vân giao thoa di chuyển
-
Bước 4: Tính toán kết quả
Thay các giá trị \(\Delta d\) và \(N\) vào công thức trên để tính ra bước sóng \(\lambda\). Đảm bảo rằng đơn vị của \(\lambda\) là nanomet (nm) nếu \(\Delta d\) được đo bằng milimet (mm).
Ví dụ: Nếu \(\Delta d = 0.03\) mm và \(N = 100\), thì bước sóng sẽ là:
\[ \lambda = \frac{2 \times 0.03 \text{ mm}}{100} = 0.0006 \text{ mm} = 600 \text{ nm} \] -
Bước 5: Đánh giá và xác minh
So sánh kết quả tính toán được với giá trị lý thuyết hoặc các giá trị đã biết trước đó để kiểm tra độ chính xác của thí nghiệm. Điều này giúp bạn xác định xem quá trình đo lường và tính toán có hợp lý và chính xác hay không.
Qua bài tập này, bạn đã học được cách sử dụng giao thoa kế Michelson để xác định bước sóng ánh sáng, một ứng dụng quan trọng trong các thí nghiệm quang học.

Bài Tập 2: Phân tích kết quả thí nghiệm Michelson-Morley
Thí nghiệm Michelson-Morley là một trong những thí nghiệm nổi tiếng nhất trong lịch sử vật lý, đóng vai trò quan trọng trong việc kiểm chứng thuyết tương đối của Albert Einstein. Dưới đây là các bước phân tích kết quả của thí nghiệm này.
- Bước 1: Hiểu nguyên lý hoạt động của thí nghiệm
Thí nghiệm Michelson-Morley sử dụng giao thoa kế Michelson để đo sự thay đổi về thời gian di chuyển của ánh sáng theo các hướng khác nhau. Nguyên lý cơ bản là nếu có sự tồn tại của "êtơ" (ether), tốc độ ánh sáng sẽ thay đổi tùy theo hướng di chuyển so với "êtơ".
- Bước 2: Xác định kỳ vọng ban đầu
Theo giả thuyết về "êtơ", ánh sáng di chuyển theo hướng song song với "êtơ" sẽ mất thời gian khác nhau so với ánh sáng di chuyển vuông góc với "êtơ". Vì vậy, khi thực hiện thí nghiệm, người ta kỳ vọng sẽ thấy sự dịch chuyển của các vân giao thoa do sự chênh lệch thời gian này.
- Bước 3: Quan sát kết quả thực tế
Kết quả thực tế của thí nghiệm Michelson-Morley không cho thấy sự dịch chuyển của các vân giao thoa, điều này ngụ ý rằng không có sự chênh lệch thời gian di chuyển của ánh sáng theo các hướng khác nhau.
- Bước 4: Phân tích và kết luận
Kết quả thí nghiệm đã khiến cho giả thuyết về "êtơ" bị bác bỏ và dẫn đến sự phát triển của thuyết tương đối hẹp của Einstein. Thuyết tương đối hẹp khẳng định rằng tốc độ ánh sáng là không đổi và không phụ thuộc vào chuyển động của người quan sát hay nguồn sáng.
- Bước 5: Tính toán độ chính xác của thí nghiệm
Các phép đo và tính toán trong thí nghiệm Michelson-Morley được thực hiện với độ chính xác cao. Công thức để tính sự chênh lệch về thời gian có thể được biểu diễn như sau:
\[
\Delta t = \frac{l}{c} \left( 1 + \frac{v^2}{c^2} \right)
\]
trong đó \( l \) là chiều dài cánh tay giao thoa kế, \( c \) là tốc độ ánh sáng, và \( v \) là vận tốc của Trái Đất so với "êtơ". Tuy nhiên, khi giá trị này bằng không, ta có kết luận rằng không tồn tại "êtơ".
Thí nghiệm Michelson-Morley đã mở ra một chương mới trong vật lý hiện đại, đặt nền tảng cho sự ra đời của thuyết tương đối và những hiểu biết sâu rộng về không gian và thời gian.

Bài Tập 3: Đo độ dịch chuyển nhỏ trong hệ thống quang học
Trong bài tập này, chúng ta sẽ sử dụng giao thoa kế Michelson để đo độ dịch chuyển nhỏ trong hệ thống quang học. Giao thoa kế Michelson là một dụng cụ quang học được sử dụng để đo lường các khoảng cách nhỏ bằng cách tạo ra hiện tượng giao thoa ánh sáng. Điều này cho phép chúng ta tính toán độ dịch chuyển với độ chính xác cao.
-
Chuẩn bị thiết bị:
- Giao thoa kế Michelson
- Laser He-Ne
- Gương phẳng và bản bán mạ
- Thước đo chính xác
-
Thiết lập hệ thống:
- Đặt laser He-Ne lên giá đỡ và điều chỉnh sao cho tia laser chiếu thẳng vào gương đầu tiên \(G_1\) và phản xạ lại đúng vị trí ban đầu.
- Đặt gương thứ hai \(G_2\) sao cho các tia sáng phản xạ từ \(G_1\) và \(G_2\) trùng nhau.
- Điều chỉnh bản bán mạ P để tạo ra hiện tượng giao thoa trên màn hình.
-
Tiến hành đo lường:
- Di chuyển gương \(G_1\) một khoảng nhỏ bằng cách xoay vít micrometer trên giao thoa kế.
- Quan sát số lượng vân giao thoa dịch chuyển trên màn hình. Ghi lại số vân giao thoa \(N\) đã dịch chuyển và độ dịch chuyển của gương \(d\).
-
Tính toán độ dịch chuyển:
Sử dụng công thức:
\[ d = \frac{N \lambda}{2} \]trong đó:
- \(d\) là độ dịch chuyển của gương
- \(N\) là số vân giao thoa đã dịch chuyển
- \(\lambda\) là bước sóng của ánh sáng sử dụng trong thí nghiệm
Kết quả tính toán sẽ cho chúng ta giá trị chính xác của độ dịch chuyển nhỏ trong hệ thống quang học.
-
Kết luận:
Bài tập này giúp chúng ta hiểu rõ hơn về cách sử dụng giao thoa kế Michelson để đo lường các khoảng cách nhỏ trong hệ thống quang học. Phương pháp này đặc biệt hữu ích trong các ứng dụng yêu cầu độ chính xác cao, chẳng hạn như trong nghiên cứu vật lý và công nghệ quang học.
Bài Tập 4: So sánh giao thoa kế Michelson và Fabry-Perot
Trong hệ thống quang học, giao thoa kế Michelson và Fabry-Perot đều là những công cụ quan trọng để đo lường các đặc tính của sóng ánh sáng, tuy nhiên chúng có những điểm khác biệt đáng chú ý trong cấu trúc và ứng dụng.
- Cấu trúc:
- Giao thoa kế Michelson sử dụng hai gương phẳng và một nguồn sáng, với một chùm tia được chia ra và đi theo hai đường quang học khác nhau. Sau đó, hai chùm tia này được kết hợp lại để tạo ra vân giao thoa.
- Giao thoa kế Fabry-Perot có cấu trúc phức tạp hơn, bao gồm hai gương bán mạ phản xạ cao được đặt song song với nhau, cho phép chùm tia sáng đi qua nhiều lần giữa hai gương, tạo ra nhiều chùm giao thoa.
- Cơ chế hoạt động:
- Trong giao thoa kế Michelson, sự thay đổi nhỏ trong độ dài đường quang học giữa hai chùm tia sẽ dẫn đến sự dịch chuyển của các vân giao thoa, từ đó xác định các thay đổi về khoảng cách hoặc chỉ số khúc xạ.
- Giao thoa kế Fabry-Perot, nhờ vào cấu trúc nhiều lần phản xạ, có khả năng phân giải các bước sóng rất nhỏ, thích hợp cho việc đo lường các dao động tần số cao và phân tích phổ chi tiết.
- Ứng dụng:
- Giao thoa kế Michelson thường được sử dụng trong các thí nghiệm cơ bản về giao thoa, đo khoảng cách chính xác, và trong các ứng dụng như phát hiện sóng hấp dẫn.
- Giao thoa kế Fabry-Perot được sử dụng rộng rãi trong quang phổ học, nghiên cứu về tính chất quang học của vật liệu, và trong các thiết bị đo laser chính xác.
- Ưu điểm và nhược điểm:
- Michelson có cấu trúc đơn giản, dễ dàng hiệu chỉnh, nhưng độ phân giải không cao bằng Fabry-Perot.
- Fabry-Perot có độ phân giải quang học cao hơn, nhưng cấu trúc phức tạp và khó hiệu chỉnh hơn, đòi hỏi sự chính xác trong việc lắp ráp và căn chỉnh các gương.
Tóm lại, việc lựa chọn giữa giao thoa kế Michelson và Fabry-Perot phụ thuộc vào yêu cầu cụ thể của thí nghiệm hay ứng dụng mà bạn muốn thực hiện. Nếu cần đo lường khoảng cách chính xác với cấu hình đơn giản, Michelson là lựa chọn phù hợp. Ngược lại, nếu cần phân giải quang phổ hoặc nghiên cứu các hiện tượng quang học với độ chi tiết cao, Fabry-Perot sẽ là lựa chọn tối ưu.
Bài Tập 5: Tính toán độ phân giải của giao thoa kế Michelson
Giao thoa kế Michelson là một công cụ quan trọng trong các thí nghiệm quang học, đặc biệt là trong việc đo lường các khoảng cách rất nhỏ hoặc thay đổi trong chiều dài. Độ phân giải của giao thoa kế được xác định bởi khả năng của nó để phát hiện các thay đổi nhỏ trong khoảng cách giữa hai gương. Trong bài tập này, chúng ta sẽ tính toán độ phân giải của giao thoa kế Michelson dựa trên các thông số đã cho.
Bước 1: Xác định bước sóng ánh sáng
Độ phân giải của giao thoa kế Michelson phụ thuộc vào bước sóng ánh sáng sử dụng trong thí nghiệm. Ta có:
Bước 2: Xác định khoảng cách dịch chuyển nhỏ nhất
Khoảng cách nhỏ nhất mà giao thoa kế Michelson có thể đo được chính là độ dịch chuyển tương ứng với một nửa bước sóng ánh sáng. Ta tính:
Bước 3: Tính độ phân giải
Độ phân giải của giao thoa kế Michelson có thể được biểu diễn qua số bậc giao thoa (N) khi dịch chuyển một khoảng cách nhất định. Khi số bậc giao thoa được tăng lên, độ phân giải sẽ càng cao. Công thức tính độ phân giải là:
Trong đó:
- \(\lambda\): Bước sóng ánh sáng
- \(N\): Số bậc giao thoa
Bước 4: Áp dụng vào bài toán cụ thể
Giả sử ta có bước sóng ánh sáng là 500 nm và số bậc giao thoa là 100. Độ phân giải của giao thoa kế Michelson sẽ được tính như sau:
Vậy, độ phân giải của giao thoa kế Michelson trong trường hợp này là 2.5 nm, nghĩa là nó có khả năng đo được những thay đổi trong khoảng cách gương nhỏ đến 2.5 nm.
Độ phân giải cao của giao thoa kế Michelson giúp nó trở thành một công cụ cực kỳ chính xác trong các thí nghiệm quang học và các ứng dụng liên quan.
Bài Tập 6: Ứng dụng giao thoa kế Michelson trong đo sóng hấp dẫn
Giao thoa kế Michelson đã đóng vai trò quan trọng trong việc phát hiện và nghiên cứu sóng hấp dẫn, một trong những hiện tượng vật lý thú vị nhất. Dưới đây là hướng dẫn chi tiết từng bước về cách sử dụng giao thoa kế Michelson để đo sóng hấp dẫn.
- Giới thiệu về sóng hấp dẫn:
Sóng hấp dẫn là sự dao động của không-thời gian do các sự kiện vũ trụ lớn như va chạm giữa các hố đen. Chúng di chuyển qua vũ trụ và gây ra những thay đổi nhỏ trong khoảng cách giữa các vật thể. Giao thoa kế Michelson có khả năng phát hiện những biến đổi cực nhỏ này.
- Nguyên lý hoạt động của giao thoa kế Michelson:
Giao thoa kế Michelson sử dụng hiện tượng giao thoa của ánh sáng để đo những biến đổi nhỏ trong khoảng cách giữa hai gương. Khi sóng hấp dẫn đi qua, nó làm thay đổi vị trí của các gương này, tạo ra sự thay đổi trong các vân giao thoa được quan sát.
- Cấu hình của giao thoa kế:
Giao thoa kế Michelson bao gồm hai gương đặt vuông góc với nhau và một nguồn ánh sáng laser. Ánh sáng từ laser được chia thành hai tia và phản xạ lại từ hai gương, sau đó tái kết hợp để tạo ra các vân giao thoa.
Khi sóng hấp dẫn đi qua, nó gây ra sự chênh lệch rất nhỏ trong đường đi của hai tia sáng, tạo ra một sự dịch chuyển trong các vân giao thoa mà ta có thể quan sát.
- Công thức tính toán độ dịch chuyển:
Độ dịch chuyển \(\Delta d\) của các vân giao thoa có thể được tính bằng công thức:
\[
\Delta d = \frac{m \lambda}{2}
\]Trong đó:
- \(m\): Số vân giao thoa dịch chuyển
- \(\lambda\): Bước sóng của ánh sáng được sử dụng
- Ứng dụng trong phát hiện sóng hấp dẫn:
Với công nghệ hiện đại, giao thoa kế Michelson đã được sử dụng trong các thí nghiệm lớn như LIGO để phát hiện sóng hấp dẫn. Việc phát hiện sóng hấp dẫn không chỉ xác nhận các lý thuyết của Einstein mà còn mở ra một cánh cửa mới cho việc nghiên cứu vũ trụ.
Qua các bước trên, ta có thể thấy giao thoa kế Michelson là một công cụ quan trọng trong việc đo lường và nghiên cứu sóng hấp dẫn, giúp chúng ta hiểu rõ hơn về vũ trụ và các hiện tượng vật lý liên quan.
Bài Tập 7: Phân tích ảnh hưởng của góc tới và góc phản xạ trong giao thoa kế Michelson
Trong bài tập này, chúng ta sẽ phân tích ảnh hưởng của góc tới và góc phản xạ trong giao thoa kế Michelson đến quá trình tạo ra các vân giao thoa. Các yếu tố này có thể ảnh hưởng đến kết quả đo và độ chính xác của thiết bị.
1. Nguyên lý hoạt động của giao thoa kế Michelson:
- Giao thoa kế Michelson sử dụng nguyên lý giao thoa của sóng ánh sáng, trong đó một chùm sáng được chia thành hai chùm, phản xạ từ hai gương, và sau đó giao thoa tại một điểm để tạo ra các vân giao thoa.
- Góc tới và góc phản xạ tại các gương có thể thay đổi đường đi của các chùm sáng và do đó ảnh hưởng đến vị trí và hình dạng của các vân giao thoa.
2. Ảnh hưởng của góc tới và góc phản xạ:
Khi góc tới (\(\theta_i\)) thay đổi, góc phản xạ (\(\theta_r\)) cũng thay đổi theo định luật phản xạ, trong đó:
Do đó, sự thay đổi góc tới có thể dẫn đến sự thay đổi về độ dài đường đi quang học của các chùm sáng, làm thay đổi sự khác biệt về pha giữa chúng. Điều này làm thay đổi hình dạng và vị trí của các vân giao thoa. Để phân tích cụ thể, chúng ta có thể xét các trường hợp sau:
- Trường hợp 1: Góc tới bằng 0: Khi góc tới là 0, các chùm sáng phản xạ trở lại theo cùng một trục, và giao thoa xảy ra theo cách thông thường, tạo ra các vân giao thoa đồng tâm.
- Trường hợp 2: Góc tới khác 0: Khi góc tới không bằng 0, các chùm sáng không còn giao thoa đồng trục, dẫn đến sự dịch chuyển của các vân giao thoa. Độ dịch chuyển này phụ thuộc vào giá trị của góc tới.
- Trường hợp 3: Ảnh hưởng của góc phản xạ: Tương tự, khi góc phản xạ thay đổi, sự khác biệt về đường đi của các chùm sáng cũng thay đổi, dẫn đến sự thay đổi trong vị trí và số lượng các vân giao thoa.
3. Tính toán sự thay đổi vân giao thoa:
Giả sử chúng ta có một hệ giao thoa kế với các gương đặt cách nhau một khoảng \(d\). Khi góc tới thay đổi, sự khác biệt về đường đi quang học (\(\Delta L\)) giữa hai chùm sáng là:
Do đó, sự thay đổi trong số lượng vân giao thoa có thể được tính theo công thức:
trong đó \(\lambda\) là bước sóng của ánh sáng sử dụng.
Qua bài tập này, chúng ta có thể thấy rằng góc tới và góc phản xạ có ảnh hưởng đáng kể đến quá trình giao thoa và kết quả đo của giao thoa kế Michelson. Hiểu rõ và kiểm soát được các yếu tố này giúp cải thiện độ chính xác của các phép đo quang học.

Bài Tập 8: Tính toán quang lộ trong giao thoa kế Michelson
Giao thoa kế Michelson là một thiết bị quang học quan trọng trong việc phân tích các hiện tượng giao thoa ánh sáng. Một trong những ứng dụng quan trọng của nó là tính toán quang lộ giữa hai nhánh của hệ thống. Để thực hiện điều này, ta cần hiểu rõ về cấu trúc và nguyên lý hoạt động của thiết bị.
Trong giao thoa kế Michelson, quang lộ của mỗi chùm sáng được xác định bởi khoảng cách giữa tấm chia chùm và các gương phản xạ. Chúng ta có thể tính toán sự chênh lệch quang lộ giữa hai nhánh bằng công thức:
\[
\Delta L = 2(d_1 - d_2)
\]
Ở đây:
- \(\Delta L\) là sự chênh lệch quang lộ.
- \(d_1\) là khoảng cách từ tấm chia chùm đến gương thứ nhất.
- \(d_2\) là khoảng cách từ tấm chia chùm đến gương thứ hai.
Khi có sự chênh lệch về quang lộ, các vân giao thoa được tạo ra trên màn hình sẽ thay đổi. Điều này phụ thuộc vào bước sóng của ánh sáng sử dụng và sự khác biệt giữa \(d_1\) và \(d_2\).
Để tăng độ chính xác trong việc tính toán quang lộ, chúng ta có thể điều chỉnh vị trí của các gương sao cho \(d_1\) và \(d_2\) khác biệt theo một giá trị nhỏ, đồng thời đo đạc số vân sáng hoặc tối xuất hiện trên màn hình:
\[
\Delta L = m \lambda \quad \text{(vân sáng)}
\]
\[
\Delta L = (m + 0.5) \lambda \quad \text{(vân tối)}
\]
Trong đó, \(m\) là số nguyên chỉ thứ bậc của vân giao thoa và \(\lambda\) là bước sóng của ánh sáng.
Thông qua việc điều chỉnh và đo đạc này, ta có thể xác định chính xác quang lộ của hệ thống, giúp ích cho nhiều ứng dụng khác nhau trong vật lý và công nghệ.
Cuối cùng, việc nắm vững phương pháp tính toán quang lộ trong giao thoa kế Michelson không chỉ giúp hiểu rõ hơn về thiết bị mà còn mở ra nhiều hướng nghiên cứu ứng dụng trong các lĩnh vực khác nhau.
Bài Tập 9: Đánh giá sai số trong phép đo bằng giao thoa kế Michelson
Trong quá trình thực hiện các phép đo bằng giao thoa kế Michelson, việc đánh giá và kiểm soát sai số là rất quan trọng để đảm bảo tính chính xác của kết quả. Các sai số này có thể phát sinh từ nhiều nguồn khác nhau, và chúng ta cần phân tích chúng một cách chi tiết để cải thiện độ tin cậy của phép đo.
- Sai số hệ thống: Đây là loại sai số xuất hiện do sự không hoàn hảo của thiết bị hoặc do điều kiện đo đạc không lý tưởng. Ví dụ, điểm 0 của thang đo không chính xác hoặc do sự dịch chuyển không đồng đều của các gương trong giao thoa kế. Sai số hệ thống có thể được hiệu chỉnh bằng cách thực hiện các điều chỉnh phù hợp trên thiết bị.
- Sai số ngẫu nhiên: Loại sai số này xuất hiện do các yếu tố ngẫu nhiên, chẳng hạn như dao động nhiệt độ hoặc độ nhạy của các thiết bị cảm biến. Sai số ngẫu nhiên khó kiểm soát hơn và thường được xử lý bằng cách thực hiện nhiều phép đo và tính giá trị trung bình.
Sai số trong phép đo có thể được đánh giá theo các bước sau:
- Tính sai số tuyệt đối: Sai số tuyệt đối được tính dựa trên sự khác biệt giữa giá trị đo được và giá trị trung bình. Công thức để tính sai số tuyệt đối là:
- Tính giá trị trung bình của sai số: Để giảm thiểu ảnh hưởng của các sai số ngẫu nhiên, chúng ta có thể tính giá trị trung bình của các lần đo:
- Sai số tuyệt đối trung bình: Sai số tuyệt đối trung bình của \(n\) lần đo được tính bằng công thức:
- Sai số dụng cụ: Đây là sai số liên quan đến độ chính xác của thiết bị đo và thường được ước lượng dựa trên độ chia nhỏ nhất của thang đo:
- Tổng sai số: Tổng sai số của phép đo là tổng của sai số tuyệt đối trung bình và sai số dụng cụ:
- Kết quả đo: Cuối cùng, kết quả đo lường sẽ được trình bày dưới dạng:
\[ \Delta A_i = |\bar{A} - A_i| \]
\[ \bar{A} = \dfrac{A_1 + A_2 + \dots + A_n}{n} \]
\[ \bar{\Delta A} = \dfrac{\Delta A_1 + \Delta A_2 + \dots + \Delta A_n}{n} \]
\[ \Delta A' = \text{nửa hoặc một độ chia nhỏ nhất của thiết bị} \]
\[ \Delta A = \bar{\Delta A} + \Delta A' \]
\[ A = \bar{A} \pm \Delta A \]
Trong đó, \( \Delta A \) là tổng sai số và \( \bar{A} \) là giá trị trung bình của các lần đo.
Việc đánh giá sai số trong các phép đo bằng giao thoa kế Michelson giúp chúng ta hiểu rõ hơn về độ chính xác và độ tin cậy của kết quả đo lường, từ đó có thể thực hiện các điều chỉnh cần thiết để giảm thiểu các sai số này.
Bài Tập 10: Thiết kế một thí nghiệm sử dụng giao thoa kế Michelson để đo tốc độ ánh sáng
Trong bài tập này, chúng ta sẽ thiết kế một thí nghiệm sử dụng giao thoa kế Michelson để đo tốc độ ánh sáng. Thí nghiệm này sẽ bao gồm các bước sau:
- Chuẩn bị thiết bị:
- Một nguồn sáng laser có bước sóng \(\lambda\).
- Giao thoa kế Michelson với các thành phần chính gồm: gương cố định, gương di động, và bộ tách chùm sáng.
- Một màn hình quan sát các vân giao thoa.
- Thiết lập thí nghiệm:
Đặt nguồn sáng laser sao cho chùm sáng ban đầu được chia thành hai chùm tại bộ tách chùm sáng. Một chùm sẽ phản xạ qua gương cố định, và chùm còn lại sẽ phản xạ qua gương di động. Hai chùm sáng này sau đó sẽ gặp lại nhau và giao thoa trên màn hình.
- Đo đạc:
Di chuyển gương di động một khoảng cách \(d\) và đếm số vân giao thoa \(N\) xuất hiện hoặc biến mất. Sử dụng công thức sau để xác định khoảng cách di chuyển của chùm sáng:
\[ \Delta d = \frac{N \cdot \lambda}{2} \]Trong đó:
- \(N\): Số vân giao thoa thay đổi.
- \(\lambda\): Bước sóng của ánh sáng laser.
- \(\Delta d\): Khoảng cách di chuyển của gương.
- Tính toán tốc độ ánh sáng:
Sử dụng công thức liên hệ giữa tốc độ ánh sáng \(c\), tần số \(f\), và bước sóng \(\lambda\) của nguồn sáng:
\[ c = f \cdot \lambda \]Trong thí nghiệm này, bạn có thể xác định \(c\) bằng cách sử dụng tần số của nguồn sáng và giá trị của bước sóng đo được.
- Đánh giá kết quả:
So sánh giá trị tốc độ ánh sáng đo được với giá trị lý thuyết \(c = 3 \times 10^8 \, \text{m/s}\). Đánh giá các sai số có thể xảy ra trong quá trình thí nghiệm, bao gồm sai số từ thiết bị và phương pháp đo.
Thí nghiệm này giúp hiểu rõ hơn về nguyên tắc hoạt động của giao thoa kế Michelson và cung cấp một phương pháp thực tế để đo tốc độ ánh sáng, một trong những hằng số vật lý quan trọng nhất.