Cực Tiểu Giao Thoa: Khám Phá Hiện Tượng Và Ứng Dụng Thực Tế

Hiện tượng giao thoa là một trong những khái niệm quan trọng trong vật lý, đặc biệt là trong nghiên cứu về sóng. Khi hai sóng gặp nhau, chúng có thể tương tác với nhau tạo nên các điểm cực đại và cực tiểu trong giao thoa. Điểm cực tiểu giao thoa là những vị trí mà biên độ của sóng tổng hợp là nhỏ nhất hoặc bằng không, tức là tại đó hai sóng triệt tiêu lẫn nhau.

1. Khái Niệm Về Cực Tiểu Giao Thoa

Cực tiểu giao thoa xảy ra khi hai sóng gặp nhau ở các vị trí mà biên độ của chúng đối ngược nhau, dẫn đến hiện tượng triệt tiêu. Hiện tượng này thường được sử dụng trong các bài toán sóng, quang học, và âm học để tính toán khoảng cách giữa các vân giao thoa và phân tích các mẫu giao thoa.

2. Công Thức Tính Toán Cực Tiểu Giao Thoa

Điểm cực tiểu trong giao thoa sóng xảy ra tại những vị trí mà:

Trong đó:

• \(\Delta d\) là hiệu đường đi của hai sóng đến một điểm.
• \(\lambda\) là bước sóng của sóng.
• \(k\) là số nguyên (0, 1, 2,...).

3. Ứng Dụng Thực Tiễn

Hiện tượng cực tiểu giao thoa không chỉ có giá trị lý thuyết mà còn được ứng dụng rộng rãi trong thực tế. Trong công nghệ quang học, nó được sử dụng để chế tạo các thiết bị như kính hiển vi giao thoa, các thiết bị đo lường chính xác, và thậm chí trong các hệ thống âm thanh để giảm thiểu nhiễu sóng.

4. Ví Dụ Minh Họa

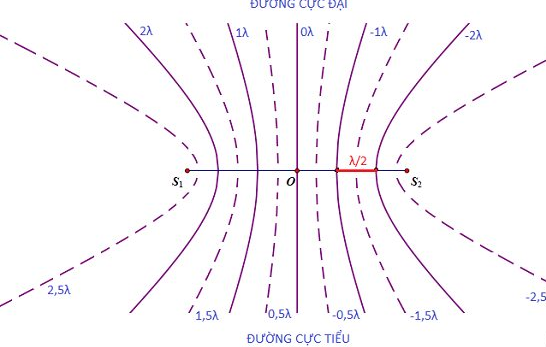
Trong bài toán giao thoa trên mặt nước, các điểm cực tiểu thường là các điểm nằm trên đường trung trực của hai nguồn sóng, nơi mà các sóng gặp nhau và triệt tiêu lẫn nhau. Nếu hai nguồn sóng cách nhau một khoảng cách \(d\), thì khoảng cách giữa các điểm cực tiểu liên tiếp là:

5. Kết Luận

Cực tiểu giao thoa là một khái niệm cơ bản trong nghiên cứu sóng, có vai trò quan trọng trong việc hiểu rõ hơn về bản chất của sóng và các hiện tượng liên quan. Nó không chỉ giúp giải thích các hiện tượng tự nhiên mà còn có nhiều ứng dụng trong công nghệ và đời sống.

Cực tiểu giao thoa là hiện tượng vật lý xuất hiện khi hai sóng kết hợp tại một điểm với độ lệch pha sao cho chúng triệt tiêu lẫn nhau, tạo ra điểm có biên độ nhỏ nhất, gọi là cực tiểu.

Trong quá trình giao thoa, hai sóng kết hợp tại điểm \(P\) sao cho hiệu đường đi của chúng là một bội số lẻ của nửa bước sóng, tức là:

\[ \Delta d = \left(2n + 1\right) \frac{\lambda}{2} \]

Ở đây:

• \(\Delta d\) là hiệu đường đi giữa hai sóng.
• \(n\) là số nguyên bất kỳ.
• \(\lambda\) là bước sóng của hai sóng giao thoa.

Hiện tượng cực tiểu giao thoa thường được quan sát rõ ràng trong các thí nghiệm giao thoa ánh sáng, sóng nước hoặc sóng âm.

Ví dụ, trong thí nghiệm khe Young, các điểm cực tiểu trên màn hình sẽ xuất hiện ở những vị trí mà khoảng cách từ các khe đến điểm đó chênh lệch đúng một nửa bước sóng, tạo ra những dải tối trên màn giao thoa.

Cực tiểu giao thoa đóng vai trò quan trọng trong nhiều ứng dụng thực tế như phân tích cấu trúc vật liệu, đo đạc chính xác trong quang học và kiểm tra chất lượng bề mặt trong công nghiệp.

Cực tiểu giao thoa không chỉ là một hiện tượng lý thuyết mà còn có nhiều ứng dụng thực tế quan trọng trong các lĩnh vực như quang học, công nghiệp, và y học.

Dưới đây là một số ứng dụng tiêu biểu:

• Phân tích quang học: Cực tiểu giao thoa được sử dụng để kiểm tra và phân tích chất lượng của các bề mặt quang học. Bằng cách đo các cực tiểu và cực đại giao thoa trên bề mặt, người ta có thể xác định độ nhám, độ phẳng, và các khiếm khuyết trên bề mặt với độ chính xác cao.
• Kiểm tra cấu trúc vật liệu: Trong ngành công nghiệp, hiện tượng cực tiểu giao thoa được áp dụng để kiểm tra các lớp màng mỏng, xác định độ dày và tính đồng nhất của các lớp vật liệu.
• Chụp ảnh giao thoa: Phương pháp chụp ảnh bằng giao thoa (interferometry) sử dụng cực tiểu giao thoa để tạo ra hình ảnh có độ phân giải cao, được ứng dụng trong nghiên cứu khoa học và y học, đặc biệt trong việc tạo ảnh 3D và kiểm tra mô học.
• Đo lường chính xác: Cực tiểu giao thoa cũng được dùng trong các thiết bị đo lường chính xác như interferometer để đo khoảng cách, độ dày, và các thông số khác với độ chính xác cực kỳ cao.

Ứng dụng của cực tiểu giao thoa đã và đang đóng góp tích cực trong nhiều lĩnh vực công nghệ và khoa học, giúp nâng cao hiệu quả sản xuất và nghiên cứu.

Trong hiện tượng giao thoa, cực tiểu giao thoa xảy ra tại các vị trí mà sóng từ hai nguồn giao thoa triệt tiêu lẫn nhau. Để tính toán các vị trí này, ta sử dụng phương trình cơ bản sau:

Khi hai sóng có cùng tần số và biên độ giao thoa, vị trí cực tiểu được xác định bởi điều kiện:

\[
d \cdot \sin(\theta) = (k + \frac{1}{2})\lambda
\]

Trong đó:

• \(d\): Khoảng cách giữa hai khe hoặc hai nguồn sóng.
• \(\theta\): Góc lệch so với phương pháp tuyến (góc tạo bởi đường thẳng nối hai khe và tia sáng).
• \(\lambda\): Bước sóng của sóng giao thoa.
• \(k\): Số nguyên, xác định thứ tự của cực tiểu (k = 0, 1, 2, ...).

Các bước tính toán vị trí cực tiểu giao thoa:

1. Xác định các thông số: \(d\), \(\lambda\), và thứ tự \(k\) của cực tiểu cần tìm.
2. Áp dụng phương trình \[d \cdot \sin(\theta) = (k + \frac{1}{2})\lambda\] để tìm góc \(\theta\).
3. Sử dụng \(\theta\) để tính khoảng cách từ vị trí cực tiểu đến tâm màn giao thoa, nếu cần.

Với các bước trên, bạn có thể tính toán chính xác vị trí của cực tiểu giao thoa trong các thí nghiệm hoặc ứng dụng thực tế liên quan đến hiện tượng này.

Dưới đây là các dạng bài tập phổ biến về hiện tượng cực tiểu giao thoa, giúp học sinh hiểu sâu hơn về khái niệm và ứng dụng thực tiễn:

1. Bài tập tính toán góc lệch \(\theta\) tại vị trí cực tiểu:
   • Cho biết khoảng cách giữa hai khe, bước sóng \(\lambda\) và thứ tự cực tiểu \(k\). Tính toán góc lệch \(\theta\).
   • Ví dụ: Tìm góc lệch \(\theta\) tại cực tiểu thứ nhất (\(k=0\)) khi khoảng cách giữa hai khe là 0.5mm và bước sóng ánh sáng là 600nm.
2. Bài tập xác định vị trí cực tiểu trên màn:
   • Cho khoảng cách từ khe đến màn, bước sóng, và khoảng cách giữa hai khe. Tính vị trí của các cực tiểu trên màn.
   • Ví dụ: Tính vị trí cực tiểu thứ hai (\(k=1\)) trên màn cách hai khe 1m, biết rằng khoảng cách giữa hai khe là 0.5mm và bước sóng ánh sáng là 600nm.
3. Bài tập liên quan đến số lượng cực tiểu:
   • Xác định số lượng cực tiểu xuất hiện trên màn trong một khoảng cách xác định.
   • Ví dụ: Tính số lượng cực tiểu xuất hiện trong khoảng 10cm trên màn khi khoảng cách giữa hai khe là 0.5mm và bước sóng ánh sáng là 600nm.
4. Bài tập về ảnh hưởng của bước sóng đến vị trí cực tiểu:
   • So sánh vị trí cực tiểu khi sử dụng ánh sáng có bước sóng khác nhau.
   • Ví dụ: So sánh vị trí cực tiểu thứ nhất (\(k=0\)) khi sử dụng ánh sáng đỏ (\(\lambda = 700nm\)) và ánh sáng tím (\(\lambda = 400nm\)).
5. Bài tập về sự thay đổi của khoảng cách giữa hai khe:
   • Xác định sự thay đổi vị trí cực tiểu khi thay đổi khoảng cách giữa hai khe.
   • Ví dụ: Tính sự thay đổi vị trí cực tiểu khi khoảng cách giữa hai khe thay đổi từ 0.5mm đến 1mm.
6. Bài tập xác định cực tiểu trong giao thoa của sóng âm:
   • Xác định vị trí cực tiểu trong giao thoa sóng âm khi biết tần số và khoảng cách giữa hai nguồn âm.
   • Ví dụ: Tính vị trí cực tiểu thứ ba (\(k=2\)) khi tần số âm là 1000Hz và khoảng cách giữa hai nguồn là 1m.
7. Bài tập về cực tiểu trong giao thoa của sóng nước:
   • Xác định vị trí cực tiểu trong giao thoa sóng nước khi biết tần số sóng và khoảng cách giữa hai nguồn sóng.
   • Ví dụ: Tính vị trí cực tiểu thứ hai (\(k=1\)) trên bề mặt nước khi tần số sóng là 2Hz và khoảng cách giữa hai nguồn sóng là 1.5m.
8. Bài tập kết hợp giữa cực đại và cực tiểu giao thoa:
   • So sánh và xác định vị trí giữa cực đại và cực tiểu trong cùng một hệ thống giao thoa.
   • Ví dụ: Xác định vị trí giao thoa cực đại và cực tiểu gần nhất khi khoảng cách giữa hai khe là 0.5mm và bước sóng ánh sáng là 600nm.
9. Bài tập về điều kiện để có cực tiểu:
   • Xác định các điều kiện cần thiết để xuất hiện cực tiểu trong hệ giao thoa.
   • Ví dụ: Tìm điều kiện của khoảng cách giữa hai khe và bước sóng để có cực tiểu thứ ba (\(k=2\)).
10. Bài tập mô phỏng cực tiểu giao thoa trên máy tính:
    • Sử dụng phần mềm mô phỏng để xác định và minh họa các vị trí cực tiểu giao thoa.
    • Ví dụ: Sử dụng phần mềm mô phỏng để xác định vị trí cực tiểu thứ nhất (\(k=0\)) khi khoảng cách giữa hai khe là 0.5mm và bước sóng ánh sáng là 600nm.

Các dạng bài tập trên không chỉ giúp học sinh nắm vững lý thuyết mà còn cung cấp công cụ để áp dụng vào các tình huống thực tế liên quan đến hiện tượng giao thoa ánh sáng.