Chủ đề hiện tượng giao thoa sóng xảy ra khi có: Hiện tượng giao thoa sóng xảy ra khi có sự gặp gỡ của hai hoặc nhiều sóng tại một điểm, tạo ra hiện tượng giao thoa với các đặc điểm đặc trưng. Bài viết này sẽ giúp bạn hiểu rõ về các điều kiện cần thiết để xảy ra hiện tượng giao thoa sóng và ứng dụng thực tế của nó trong cuộc sống.
Mục lục
Hiện Tượng Giao Thoa Sóng
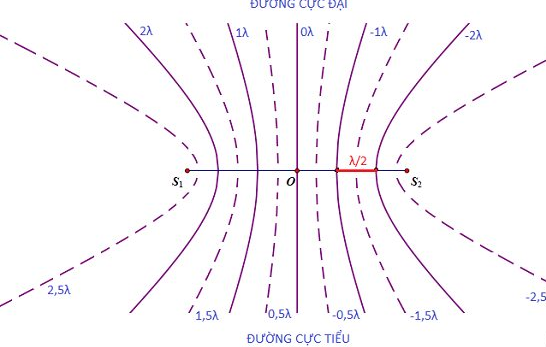
Hiện tượng giao thoa sóng xảy ra khi hai hoặc nhiều sóng gặp nhau tại một điểm và kết hợp với nhau, tạo ra các điểm có biên độ dao động cực đại hoặc cực tiểu. Đây là một hiện tượng quan trọng trong vật lý, có thể xảy ra với các loại sóng khác nhau như sóng nước, sóng âm, và sóng ánh sáng.
Điều Kiện Xảy Ra Hiện Tượng Giao Thoa Sóng
- Các nguồn sóng phải có tần số và độ lệch pha không đổi theo thời gian.
- Các nguồn sóng phải có biên độ tương đương hoặc gần bằng nhau.
- Các sóng phải gặp nhau tại một điểm trong không gian để tương tác.
Công Thức Biểu Diễn Sóng Giao Thoa
Phương trình sóng tại điểm giao thoa được mô tả bởi công thức:
\[ y = 2A \cos \left( \frac{\Delta \phi}{2} \right) \cos \left( \omega t + \frac{\Delta \phi}{2} \right) \]
Trong đó:
- \( A \) là biên độ của mỗi sóng thành phần.
- \( \Delta \phi \) là độ lệch pha giữa hai sóng.
- \( \omega \) là tần số góc của sóng.
- \( t \) là thời gian.
Hiện Tượng Tăng Cường và Triệt Tiêu
| Hiện tượng | Điều kiện | Biên độ tổng hợp |
| Tăng cường | \( \Delta d = k\lambda \) | \( A_{max} = 2A \) |
| Triệt tiêu | \( \Delta d = (k + \frac{1}{2})\lambda \) | \[ A_{min} = 0 \] |
Ứng Dụng Của Hiện Tượng Giao Thoa Sóng
- Đo bước sóng của ánh sáng trong các thí nghiệm vật lý.
- Ứng dụng trong công nghệ truyền thông và xử lý tín hiệu.
- Ứng dụng trong nghiên cứu và phát triển công nghệ sóng âm.

.png)
Tổng Quan Về Hiện Tượng Giao Thoa Sóng
Hiện tượng giao thoa sóng là một trong những biểu hiện rõ rệt của tính chất sóng trong vật lý, xảy ra khi hai hay nhiều sóng gặp nhau và kết hợp để tạo ra một mô hình giao thoa phức tạp. Hiện tượng này có thể quan sát được khi các sóng kết hợp từ hai nguồn đồng bộ gặp nhau tại một điểm trong không gian.
Để hiểu rõ hơn về giao thoa sóng, cần xem xét sự kết hợp của hai sóng đơn giản có cùng tần số và biên độ, nhưng có thể có sự khác biệt về pha. Phương trình tổng quát của sóng tại điểm giao thoa có dạng:
Trong đó:
- \(A\) là biên độ của mỗi sóng thành phần.
- \(\Delta \phi\) là độ lệch pha giữa hai sóng.
- \(\omega\) là tần số góc của sóng.
- \(t\) là thời gian.
Nếu hai sóng có cùng pha (\(\Delta \phi = 0\)), chúng sẽ tăng cường lẫn nhau, tạo ra một sóng mới có biên độ lớn hơn:
Ngược lại, nếu hai sóng ngược pha (\(\Delta \phi = \pi\)), chúng sẽ triệt tiêu lẫn nhau, làm cho biên độ tổng hợp tại điểm đó bằng không:
Điều này giải thích tại sao trên bề mặt nước, khi hai sóng kết hợp, chúng ta có thể thấy các vân sáng và vân tối xen kẽ – các vùng mà sóng nước tăng cường lẫn nhau và các vùng mà chúng triệt tiêu nhau.
Hiện tượng giao thoa sóng không chỉ dừng lại ở các sóng nước mà còn có thể quan sát được với sóng ánh sáng, âm thanh, và thậm chí là sóng vô tuyến, làm nền tảng cho nhiều ứng dụng khoa học và kỹ thuật hiện đại.
Các Dạng Bài Tập Về Hiện Tượng Giao Thoa Sóng
Dưới đây là các dạng bài tập cơ bản và nâng cao về hiện tượng giao thoa sóng mà học sinh cần nắm vững để có thể hiểu sâu về hiện tượng này và áp dụng vào thực tế:
-
Dạng 1: Xác định vị trí các vân giao thoa.
Yêu cầu học sinh xác định vị trí của các vân sáng và vân tối trên một màn giao thoa, sử dụng công thức tính khoảng cách giữa các vân:
\[ \Delta x = \frac{\lambda D}{a} \]Trong đó:
- \(\Delta x\) là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp.
- \(\lambda\) là bước sóng của sóng.
- \(D\) là khoảng cách từ hai nguồn đến màn.
- \(a\) là khoảng cách giữa hai nguồn.
-
Dạng 2: Tính số vân giao thoa.
Bài tập yêu cầu tính số lượng vân sáng và vân tối trong một khoảng nhất định trên màn giao thoa:
\[ n = \frac{2D \sin \theta}{\lambda} \]Trong đó:
- \(n\) là số lượng vân giao thoa.
- \(D\) là khoảng cách từ hai nguồn đến màn.
- \(\theta\) là góc tạo bởi đường nối từ nguồn đến màn và đường vuông góc với màn.
- \(\lambda\) là bước sóng của sóng.
-
Dạng 3: Xác định biên độ dao động tại một điểm.
Bài tập yêu cầu tính toán biên độ dao động tổng hợp tại một điểm giao thoa, khi biết biên độ của các sóng thành phần:
\[ A = 2A_0 \cos\left(\frac{\Delta \phi}{2}\right) \]Trong đó:
- \(A_0\) là biên độ của các sóng thành phần.
- \(\Delta \phi\) là độ lệch pha giữa hai sóng.
-
Dạng 4: Tính pha của sóng tại một điểm.
Bài tập này yêu cầu xác định pha của sóng tổng hợp tại một điểm khi biết pha của các sóng thành phần:
\[ \phi = \phi_1 + \phi_2 \]Trong đó:
- \(\phi_1\) và \(\phi_2\) là pha của các sóng thành phần.
-
Dạng 5: Tính cường độ sóng tại một điểm.
Bài tập yêu cầu xác định cường độ của sóng tại một điểm dựa trên biên độ của các sóng thành phần:
\[ I = I_0 \cos^2\left(\frac{\Delta \phi}{2}\right) \]Trong đó:
- \(I\) là cường độ của sóng tại điểm đó.
- \(I_0\) là cường độ của sóng thành phần.
- \(\Delta \phi\) là độ lệch pha giữa hai sóng.
-
Dạng 6: Giao thoa sóng âm.
Bài tập liên quan đến giao thoa sóng âm, yêu cầu xác định các điểm có cường độ âm lớn nhất và nhỏ nhất trên trục giao thoa.
-
Dạng 7: Giao thoa ánh sáng trong thí nghiệm Young.
Bài tập mô phỏng thí nghiệm Young với hai khe sáng, yêu cầu xác định vị trí các vân giao thoa sáng và tối.
-
Dạng 8: Giao thoa sóng nước.
Bài tập yêu cầu mô phỏng hiện tượng giao thoa trên mặt nước khi hai nguồn sóng kết hợp.
-
Dạng 9: Giao thoa sóng điện từ.
Bài tập yêu cầu xác định các vị trí có cường độ trường điện từ lớn nhất và nhỏ nhất trong một môi trường giao thoa.
-
Dạng 10: Giao thoa sóng trong cơ học lượng tử.
Bài tập yêu cầu phân tích hiện tượng giao thoa sóng của hạt trong cơ học lượng tử, ví dụ như giao thoa electron.