Trong Thí Nghiệm Về Giao Thoa Sóng Trên Mặt Nước: Hiểu Đúng, Thực Hành Chuẩn

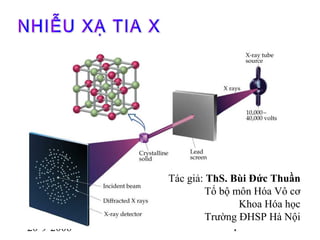
Trong vật lý, giao thoa sóng trên mặt nước là hiện tượng thú vị được sử dụng để minh họa các nguyên lý cơ bản của sóng. Khi hai nguồn sóng đồng pha đặt gần nhau trên mặt nước, chúng tạo ra các gợn sóng giao thoa. Thí nghiệm này thường được sử dụng trong các bài học vật lý để giúp học sinh hiểu rõ hơn về khái niệm giao thoa và sự chồng chập của sóng.

Các Thông Số Chính Trong Thí Nghiệm

• Tần số nguồn sóng: Tần số dao động của các nguồn sóng ảnh hưởng đến khoảng cách giữa các vân giao thoa. Ví dụ, với tần số \(f = 30\text{Hz}\), các vân giao thoa sẽ có khoảng cách ngắn hơn so với tần số thấp hơn.
• Khoảng cách giữa các nguồn: Khoảng cách giữa hai nguồn sóng cũng ảnh hưởng trực tiếp đến mô hình giao thoa. Khoảng cách này càng nhỏ thì các vân giao thoa càng dày.
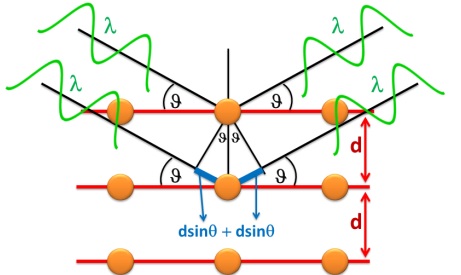
• Bước sóng \(\lambda\): Bước sóng được tính theo công thức \(\lambda = \dfrac{v}{f}\), trong đó \(v\) là vận tốc truyền sóng và \(f\) là tần số dao động.

Mô Hình Giao Thoa Sóng

Khi hai sóng từ hai nguồn đồng pha gặp nhau trên mặt nước, chúng sẽ giao thoa tạo nên các điểm giao thoa tăng cường và giao thoa triệt tiêu. Các điểm này được gọi là các vân sáng (giao thoa tăng cường) và vân tối (giao thoa triệt tiêu). Mô hình giao thoa này có thể được quan sát rõ ràng trên mặt nước bằng cách sử dụng đèn laser hoặc ánh sáng khác chiếu vào.

Ứng Dụng Của Thí Nghiệm

• Giúp học sinh hiểu rõ hơn về các khái niệm sóng và giao thoa trong vật lý.
• Ứng dụng trong việc đo bước sóng của sóng nước.
• Sử dụng để minh họa các nguyên lý cơ bản của giao thoa ánh sáng và sóng cơ học.

Thí nghiệm này không chỉ là một công cụ giáo dục mạnh mẽ mà còn là một minh chứng rõ ràng về sự kỳ diệu của các hiện tượng tự nhiên. Giao thoa sóng trên mặt nước là một hiện tượng dễ quan sát, dễ hiểu, và có nhiều ứng dụng thực tiễn trong đời sống cũng như trong nghiên cứu khoa học.

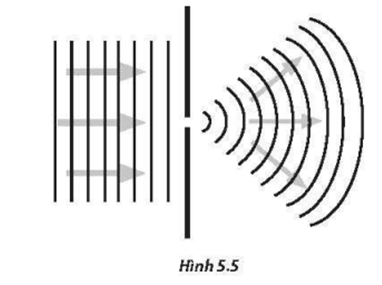
Giao thoa sóng là một hiện tượng thú vị xảy ra khi hai hay nhiều sóng gặp nhau và tương tác với nhau trên mặt nước. Trong thí nghiệm, hiện tượng này thường được quan sát khi ta tạo ra hai nguồn sóng và theo dõi cách các sóng từ hai nguồn này giao thoa, tạo ra các vân sáng và vân tối trên mặt nước.

• Đầu tiên, ta cần chuẩn bị hai nguồn sóng đồng nhất, được đặt cách nhau một khoảng nhất định.
• Sau đó, cả hai nguồn sóng sẽ được kích thích đồng thời, tạo ra các sóng lan truyền trên mặt nước.
• Khi các sóng này gặp nhau, chúng sẽ tạo ra hiện tượng giao thoa, nơi mà tại một số điểm, các sóng tăng cường lẫn nhau (vân sáng), và tại các điểm khác, chúng triệt tiêu lẫn nhau (vân tối).

Giao thoa sóng giúp ta hiểu rõ hơn về các tính chất của sóng, như bước sóng, tần số, và cách mà các sóng tương tác với nhau trong môi trường thực tế. Đây là một trong những hiện tượng cơ bản, đóng vai trò quan trọng trong việc nghiên cứu các tính chất vật lý của sóng.

Các thí nghiệm về giao thoa sóng trên mặt nước giúp minh họa rõ ràng hiện tượng sóng và cách chúng tương tác với nhau. Dưới đây là một số bước cơ bản để thực hiện thí nghiệm này.

1. Chuẩn bị dụng cụ:
   • Một bể chứa nước cạn.
   • Hai nguồn sóng cơ học (có thể là hai chiếc đinh ghim hoặc que nhỏ).
   • Một thiết bị tạo dao động để kích thích nguồn sóng.
2. Thiết lập thí nghiệm:
   • Đặt hai nguồn sóng cách nhau một khoảng nhất định trên mặt nước.
   • Kích hoạt thiết bị dao động để cả hai nguồn bắt đầu tạo sóng trên mặt nước.
3. Quan sát hiện tượng giao thoa:
   • Các sóng từ hai nguồn sẽ lan truyền và gặp nhau tại nhiều điểm trên mặt nước.
   • Những nơi các đỉnh sóng gặp nhau sẽ tạo ra các vân sáng (sóng tăng cường), và nơi đỉnh gặp đáy sẽ tạo ra các vân tối (sóng triệt tiêu).
4. Ghi nhận kết quả:
   • Sử dụng máy quay hoặc chụp ảnh để ghi lại các vân giao thoa.
   • Phân tích khoảng cách giữa các vân để xác định bước sóng và các đặc tính khác của sóng.

Thí nghiệm này không chỉ giúp hiểu rõ hơn về hiện tượng giao thoa sóng mà còn có thể ứng dụng trong nhiều lĩnh vực khác nhau như vật lý học, kỹ thuật và công nghệ sóng.

Mô hình giao thoa sóng là một trong những khái niệm quan trọng trong vật lý, thể hiện cách các sóng tương tác với nhau khi gặp gỡ. Hiện tượng này không chỉ xuất hiện trên mặt nước mà còn trong nhiều lĩnh vực khác như âm thanh, ánh sáng, và sóng điện từ. Dưới đây là một cái nhìn tổng quan về mô hình này và các ứng dụng thực tiễn của nó.

1. Mô Hình Giao Thoa Sóng
   • Mô hình này giải thích cách các sóng từ hai nguồn gặp nhau, tạo nên các vùng giao thoa với những đặc trưng như vân sáng (sóng tăng cường) và vân tối (sóng triệt tiêu).
   • Sự hình thành các vân giao thoa phụ thuộc vào khoảng cách giữa các nguồn sóng, bước sóng, và pha ban đầu của sóng.
   • Các vân sáng xuất hiện tại những điểm mà sóng từ hai nguồn đồng pha, trong khi các vân tối xuất hiện tại các điểm mà sóng từ hai nguồn ngược pha.
2. Các Ứng Dụng Thực Tiễn
   • Trong công nghệ sóng âm: Giao thoa sóng âm được ứng dụng trong thiết kế phòng thu, phòng hòa nhạc để tối ưu hóa chất lượng âm thanh.
   • Trong quang học: Giao thoa ánh sáng được sử dụng trong các thí nghiệm xác định bước sóng của ánh sáng, chế tạo các thiết bị đo lường chính xác như giao thoa kế.
   • Trong viễn thông: Nguyên lý giao thoa được áp dụng trong truyền thông bằng sóng radio, giúp cải thiện tín hiệu và giảm nhiễu.
   • Trong y học: Giao thoa sóng siêu âm được sử dụng để hình ảnh hóa các cơ quan nội tạng và chẩn đoán bệnh lý.
   • Trong nghiên cứu khoa học: Hiện tượng giao thoa là nền tảng cho nhiều thí nghiệm trong vật lý, từ nghiên cứu các hạt cơ bản đến khám phá vũ trụ.

Qua mô hình giao thoa sóng, chúng ta không chỉ hiểu sâu hơn về bản chất của sóng mà còn tìm ra nhiều ứng dụng thiết thực, đóng góp quan trọng trong đời sống và các ngành công nghiệp.

1. Bài tập 1: Tính toán khoảng cách giữa các vân giao thoa

   Hai nguồn sóng \(S_1\) và \(S_2\) dao động với cùng tần số trên mặt nước, khoảng cách giữa chúng là \(d = 10\) cm. Bước sóng là \(\lambda = 2\) cm. Hãy tính khoảng cách giữa các vân sáng liên tiếp.

   Lời giải: Khoảng cách giữa hai vân sáng liên tiếp là \( \Delta x = \frac{\lambda}{2} = 1 \) cm.

2. Bài tập 2: Xác định vị trí vân tối thứ 3

   Hai nguồn sóng cách nhau 20 cm, dao động đồng pha với bước sóng là 4 cm. Xác định vị trí vân tối thứ 3 trên mặt nước.

   Lời giải: Vị trí vân tối thứ 3 được tính bằng công thức \( x_3 = \frac{(2k+1)\lambda}{2} = 18 \) cm.

3. Bài tập 3: Tính số vân sáng trong một khoảng nhất định

   Cho biết khoảng cách giữa hai nguồn sóng là 15 cm và bước sóng là 1.5 cm. Tính số vân sáng xuất hiện trên đoạn thẳng nối hai nguồn.

   Lời giải: Số vân sáng \( n = \frac{d}{\lambda} + 1 = 11 \) vân.

4. Bài tập 4: Tính khoảng cách giữa hai điểm dao động cùng pha

   Hai nguồn phát sóng cách nhau 25 cm. Bước sóng của sóng là 5 cm. Tính khoảng cách giữa hai điểm trên mặt nước dao động cùng pha.

   Lời giải: Khoảng cách giữa hai điểm dao động cùng pha là \( d = n\lambda = 25 \) cm.

5. Bài tập 5: Xác định biên độ tổng hợp tại một điểm

   Hai nguồn sóng có cùng biên độ phát ra sóng với tần số 50 Hz, bước sóng 2 cm. Tính biên độ dao động tại điểm M cách hai nguồn lần lượt 6 cm và 4 cm.

   Lời giải: Biên độ tại điểm M là \( A = 2A_0\cos\left(\frac{2\pi}{\lambda}\times \frac{\Delta d}{2}\right) \).

6. Bài tập 6: Tính tần số sóng từ độ lệch pha

   Một nguồn sóng dao động với biên độ 0.5 cm. Độ lệch pha giữa hai điểm M và N là 90 độ. Tính tần số của sóng nếu khoảng cách từ M đến N là 2 cm.

   Lời giải: Tần số của sóng \( f = \frac{\Delta \phi}{2\pi \times d/\lambda} \).

7. Bài tập 7: Xác định vị trí vân sáng khi tăng bước sóng

   Hai nguồn sóng cách nhau 12 cm. Nếu bước sóng tăng từ 1 cm lên 2 cm, vị trí vân sáng thứ 4 thay đổi như thế nào?

   Lời giải: Vị trí vân sáng thứ 4 thay đổi theo công thức \( x_4 = \frac{4\lambda}{d} \).

8. Bài tập 8: Xác định vận tốc sóng

   Một nguồn sóng dao động với tần số 60 Hz tạo ra sóng với bước sóng 3 cm. Tính vận tốc của sóng trên mặt nước.

   Lời giải: Vận tốc sóng \( v = f \times \lambda = 180 \) cm/s.

9. Bài tập 9: Tính số vân tối trên một đoạn thẳng

   Cho hai nguồn sóng cách nhau 20 cm với bước sóng là 2 cm. Tính số vân tối trên đoạn thẳng nối hai nguồn.

   Lời giải: Số vân tối là \( n = \frac{d}{\lambda} = 10 \) vân.

10. Bài tập 10: Xác định biên độ tại giao điểm của hai sóng

    Hai nguồn sóng phát ra sóng với cùng biên độ và cùng pha. Tính biên độ tại điểm giao nhau của hai sóng trên mặt nước.

    Lời giải: Biên độ tại giao điểm là \( A_{tổng} = 2A_0 \cos(\Delta \phi / 2) \).

Trong thí nghiệm giao thoa sóng trên mặt nước, việc tính toán bước sóng là một trong những kỹ năng cơ bản nhưng quan trọng. Để xác định bước sóng \(\lambda\), bạn có thể áp dụng các công thức toán học từ dữ liệu thí nghiệm, bao gồm khoảng cách giữa các điểm trên mặt nước, tần số của sóng và vận tốc truyền sóng.

Dưới đây là các bước cơ bản để giải quyết dạng bài tập này:

1. Xác định các thông số cần thiết:
   • Vận tốc truyền sóng trên mặt nước \(v\) (m/s).
   • Tần số dao động \(f\) (Hz).
   • Khoảng cách giữa hai nguồn sóng hoặc các điểm giao thoa \(d\) (cm hoặc m).
2. Áp dụng công thức:

   Sử dụng công thức tính bước sóng:

   \[ \lambda = \frac{v}{f} \]

   Trong đó:

   • \(v\) là vận tốc truyền sóng.
   • \(f\) là tần số dao động của nguồn sóng.
3. Thay số và tính toán:

   Thay các giá trị \(v\) và \(f\) vào công thức để tính toán bước sóng \(\lambda\).

4. Đối chiếu với dữ liệu thí nghiệm:

   Sau khi tính toán, đối chiếu kết quả với dữ liệu thực tế từ thí nghiệm để xác nhận độ chính xác.

Ví dụ, nếu trong thí nghiệm bạn có vận tốc truyền sóng \(v = 20\) cm/s và tần số \(f = 5\) Hz, bước sóng sẽ được tính như sau:

Với các bước trên, bạn có thể dễ dàng tính toán được bước sóng dựa trên dữ liệu từ thí nghiệm giao thoa sóng trên mặt nước.

Trong thí nghiệm giao thoa sóng trên mặt nước, xác định khoảng cách giữa các vân giao thoa là một bước quan trọng để hiểu rõ hơn về tính chất của sóng. Khoảng cách này có thể được tính toán bằng cách sử dụng bước sóng \(\lambda\) và khoảng cách giữa hai nguồn sóng \(d\).

Các bước thực hiện cụ thể như sau:

1. Xác định các thông số:
   • Bước sóng \(\lambda\) (cm hoặc m) được tính từ Dạng 1.
   • Khoảng cách giữa hai nguồn sóng \(d\) (cm hoặc m).
   • Khoảng cách từ nguồn sóng đến điểm quan sát \(L\) (cm hoặc m).
2. Áp dụng công thức tính khoảng cách giữa các vân:

   Sử dụng công thức sau để tính khoảng cách giữa các vân giao thoa:

   \[ \Delta y = \frac{\lambda \cdot L}{d} \]

   Trong đó:

   • \(\Delta y\) là khoảng cách giữa hai vân giao thoa liên tiếp.
   • \(\lambda\) là bước sóng.
   • \(L\) là khoảng cách từ nguồn sóng đến điểm quan sát.
   • \(d\) là khoảng cách giữa hai nguồn sóng.
3. Thay số và tính toán:

   Thay các giá trị đã xác định vào công thức để tính toán khoảng cách giữa các vân.

4. Phân tích kết quả:

   Sau khi tính toán, đối chiếu với các vân thực tế quan sát được trên mặt nước để xác nhận độ chính xác của kết quả.

Ví dụ, nếu bước sóng \(\lambda = 2\) cm, khoảng cách giữa hai nguồn sóng \(d = 10\) cm và khoảng cách từ nguồn đến điểm quan sát \(L = 50\) cm, ta có:

Với cách tính này, bạn có thể xác định khoảng cách giữa các vân giao thoa một cách chính xác và hiệu quả.

Trong thí nghiệm giao thoa sóng trên mặt nước, vận tốc truyền sóng là một đại lượng quan trọng có thể được tính toán dựa trên các thông số liên quan đến tần số và bước sóng. Quá trình tính toán vận tốc sóng thường được thực hiện theo các bước sau:

Các bước tính toán vận tốc truyền sóng:

1. Bước 1: Đo tần số sóng (\(f\))

   Tần số sóng là số lần sóng lặp lại trong một giây. Trong thí nghiệm, bạn có thể sử dụng nguồn phát sóng để tạo ra sóng đều đặn trên mặt nước, sau đó đo tần số này bằng cách đếm số lần sóng lặp lại trong một khoảng thời gian nhất định.

   \[ f = \frac{N}{T} \]

   Trong đó:

   • \(f\) là tần số sóng (Hz)
   • \(N\) là số lần sóng lặp lại
   • \(T\) là thời gian thực hiện thí nghiệm (giây)
2. Bước 2: Đo bước sóng (\(\lambda\))

   Bước sóng là khoảng cách giữa hai đỉnh sóng liên tiếp. Bạn có thể đo trực tiếp bước sóng bằng cách đo khoảng cách giữa các đỉnh sóng trên mặt nước.

   \[ \lambda = \frac{D}{n} \]

   Trong đó:

   • \(\lambda\) là bước sóng (m)
   • \(D\) là khoảng cách giữa hai nguồn sóng (m)
   • \(n\) là số đỉnh sóng
3. Bước 3: Tính vận tốc sóng (\(v\))

   Sau khi đã có được giá trị tần số sóng và bước sóng, vận tốc truyền sóng có thể được tính bằng công thức sau:

   \[ v = f \cdot \lambda \]

   Trong đó:

   • \(v\) là vận tốc truyền sóng (m/s)
   • \(f\) là tần số sóng (Hz)
   • \(\lambda\) là bước sóng (m)

   Ví dụ: Nếu tần số sóng đo được là \(5 \, \text{Hz}\) và bước sóng là \(0.2 \, \text{m}\), vận tốc sóng sẽ là:

   \[ v = 5 \cdot 0.2 = 1 \, \text{m/s} \]

Phân tích kết quả:

Sau khi tính toán, bạn sẽ có được vận tốc truyền sóng. Kết quả này có thể được sử dụng để so sánh với các giá trị lý thuyết và đánh giá độ chính xác của thí nghiệm. Nếu có sự sai lệch, cần kiểm tra lại các bước đo lường và điều kiện thực hiện thí nghiệm.

Trong thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn sóng kết hợp thường dao động cùng pha, tạo ra các cực đại và cực tiểu tại những điểm nhất định trên bề mặt nước. Dưới đây là các bước phân tích mô hình giao thoa sóng dựa trên kết quả thí nghiệm.

1. Phân tích hình dạng giao thoa

• Xác định vị trí các điểm cực đại và cực tiểu trên bề mặt nước bằng cách quan sát các vòng sóng đồng tâm lan truyền từ hai nguồn.
• Phân tích mô hình giao thoa: Các điểm cực đại tương ứng với sự giao thoa tăng cường, trong khi các điểm cực tiểu là kết quả của sự giao thoa triệt tiêu.

2. Phân tích khoảng cách giữa các cực đại và cực tiểu

Khoảng cách giữa các vân giao thoa có thể được tính toán thông qua công thức:

Trong đó:

• \(\Delta x\) là khoảng cách giữa các vân giao thoa.
• \(\lambda\) là bước sóng của sóng trên mặt nước.
• D là khoảng cách từ nguồn sóng đến màn quan sát.
• d là khoảng cách giữa hai nguồn sóng.

3. Đánh giá tần số dao động

Tần số của các nguồn sóng đóng vai trò quan trọng trong việc xác định bước sóng và từ đó ảnh hưởng đến khoảng cách giữa các vân giao thoa. Giả sử hai nguồn dao động với tần số \(f = 80\ Hz\), ta có thể sử dụng công thức:

Trong đó:

• v là vận tốc truyền sóng trên mặt nước.
• f là tần số dao động của nguồn.
• \(\lambda\) là bước sóng.

4. So sánh kết quả lý thuyết với thực tế

Sau khi đo đạc và tính toán, ta so sánh khoảng cách giữa các vân giao thoa thực tế với kết quả lý thuyết. Nếu có sự sai lệch, cần xác định các yếu tố như sai số đo đạc, ảnh hưởng của môi trường (như tốc độ gió, độ sâu nước) để giải thích.

5. Ứng dụng kết quả thí nghiệm

• Hiểu biết về hiện tượng giao thoa sóng trên mặt nước có thể ứng dụng trong các nghiên cứu sóng biển, truyền thông và viễn thông.
• Kết quả của thí nghiệm cũng có thể được áp dụng trong việc thiết kế các hệ thống cảm biến dựa trên hiện tượng giao thoa.

Như vậy, qua việc phân tích mô hình giao thoa sóng từ kết quả thí nghiệm, chúng ta không chỉ hiểu rõ hơn về nguyên lý của hiện tượng giao thoa mà còn có thể ứng dụng vào nhiều lĩnh vực khác nhau trong đời sống thực tế.

Trong thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp dao động cùng pha với tần số \( f \). Tại một điểm M cách các nguồn những khoảng \( d_1 \) và \( d_2 \), sóng có biên độ cực đại. Giữa M và đường trung trực của hai nguồn có các dãy cực đại hoặc cực tiểu xen kẽ.

Dưới đây là các bước tính toán tần số sóng dựa trên dữ liệu thực nghiệm:

1. Xác định khoảng cách từ điểm M đến hai nguồn, ký hiệu là \( d_1 \) và \( d_2 \).
2. Xác định số lượng dãy cực đại (hoặc cực tiểu) giữa M và đường trung trực, ký hiệu là \( n \).
3. Sử dụng công thức giao thoa để tính bước sóng \( \lambda \):

\[
\Delta d = |d_1 - d_2| = k\lambda
\]
với \( k \) là số bậc của cực đại (hoặc cực tiểu).

4. Sử dụng vận tốc sóng \( v \) đã biết để tính tần số sóng:

\[
f = \frac{v}{\lambda}
\]

Ví dụ thực nghiệm:

• Trong thí nghiệm, hai nguồn dao động với tần số \( f = 20 \, \text{Hz} \) và cùng pha.
• Điểm M cách hai nguồn lần lượt \( d_1 = 25 \, \text{cm} \) và \( d_2 = 20 \, \text{cm} \).
• Số dãy cực tiểu giữa M và đường trung trực là 5.
• Sử dụng dữ liệu trên, ta có:

\[
\Delta d = |25 - 20| = 5 \, \text{cm}
\]

• Vận tốc truyền sóng trên mặt nước là \( v = 40 \, \text{cm/s} \).
• Do đó, bước sóng \( \lambda \) được tính như sau:

\[
\lambda = \frac{\Delta d}{k} = \frac{5 \, \text{cm}}{5} = 1 \, \text{cm}
\]

• Tần số sóng được tính bằng công thức:

\[
f = \frac{v}{\lambda} = \frac{40 \, \text{cm/s}}{1 \, \text{cm}} = 40 \, \text{Hz}
\]

Trong thí nghiệm giao thoa sóng trên mặt nước, ta sử dụng hai nguồn sóng kết hợp \( S_1 \) và \( S_2 \) dao động đồng pha với cùng tần số. Vị trí các vân giao thoa sẽ được xác định dựa trên sự chênh lệch pha giữa các sóng phát ra từ hai nguồn này.

Để xác định số lượng vân giao thoa trên một đoạn nhất định, ta cần áp dụng công thức tính số vân cực đại và số vân cực tiểu dựa vào điều kiện giao thoa như sau:

• Điều kiện vân cực đại (vân sáng): \(\Delta d = k\lambda\)
• Điều kiện vân cực tiểu (vân tối): \(\Delta d = \left( k + \frac{1}{2} \right)\lambda\)

Trong đó:

• \(\Delta d\) là độ chênh lệch quãng đường truyền của sóng từ hai nguồn tới điểm khảo sát.
• \(\lambda\) là bước sóng.
• \(k\) là số nguyên biểu thị thứ tự của vân giao thoa.

Bước đầu tiên là xác định các giá trị đầu vào:

1. Khoảng cách giữa hai nguồn sóng \( S_1 \) và \( S_2 \) (gọi là \( d \)).
2. Khoảng cách từ các nguồn sóng đến điểm cần khảo sát trên mặt nước.
3. Bước sóng \( \lambda \) của sóng trên mặt nước.

Sau khi có đủ các thông số này, ta sẽ tính số lượng vân giao thoa trong khoảng cách cần xác định.

Ví dụ:

Giả sử hai nguồn sóng cách nhau \( d = 10 \, \text{cm} \) và bước sóng của sóng là \( \lambda = 2 \, \text{cm} \). Ta cần xác định số lượng vân sáng và vân tối trên đoạn thẳng từ điểm \( M \) đến điểm \( N \), với khoảng cách giữa \( M \) và \( N \) là \( 20 \, \text{cm} \).

Ta có công thức tính số lượng vân sáng giữa hai điểm:

Thay số vào công thức:

Do đó, trên đoạn thẳng từ \( M \) đến \( N \), sẽ có tổng cộng 10 vân sáng. Số vân tối cũng có thể tính toán tương tự dựa vào khoảng cách giữa các điểm giao thoa.

Kết luận: Việc xác định số lượng vân giao thoa trên một đoạn nhất định đòi hỏi sự tính toán cẩn thận các yếu tố như bước sóng, khoảng cách giữa các nguồn sóng và khoảng cách khảo sát. Từ đó, ta có thể dễ dàng đếm được số lượng vân giao thoa một cách chính xác.

Trong thí nghiệm về giao thoa sóng trên mặt nước, sự ảnh hưởng của khoảng cách giữa các nguồn sóng đến hiện tượng giao thoa là một trong những yếu tố quan trọng cần được phân tích chi tiết. Khoảng cách này có thể ảnh hưởng đến sự xuất hiện của các dãy cực đại và cực tiểu trên mặt nước.

Một số yếu tố cần được xem xét bao gồm:

• Khoảng cách giữa các nguồn sóng \(d\)
• Tần số của sóng \(f\)
• Biên độ sóng \(A\)
• Tốc độ truyền sóng \(v\)

Giả sử hai nguồn sóng \(A\) và \(B\) dao động cùng pha, khoảng cách giữa chúng là \(d\), khi đó các điểm cực đại và cực tiểu sẽ phân bố trên mặt nước tùy thuộc vào \(d\) và bước sóng \(\lambda\).

Ta có công thức tính bước sóng:

Trong đó:

• \(v\) là tốc độ truyền sóng
• \(f\) là tần số của sóng

Khi khoảng cách giữa hai nguồn sóng \(d\) thay đổi, số lượng các dãy cực đại và cực tiểu cũng thay đổi tương ứng. Ta có công thức xác định vị trí của các điểm cực đại và cực tiểu trên mặt nước:

Điểm cực đại xuất hiện khi:

Điểm cực tiểu xuất hiện khi:

Trong đó \(k\) là một số nguyên.

Như vậy, khi khoảng cách giữa hai nguồn sóng \(d\) lớn hơn, các điểm cực đại sẽ xuất hiện thưa hơn, và ngược lại, khi khoảng cách này giảm, số lượng các điểm cực đại sẽ dày hơn trên mặt nước. Do đó, việc điều chỉnh khoảng cách giữa các nguồn sóng có thể thay đổi mô hình giao thoa.

Ví dụ minh họa: Nếu trong thí nghiệm, hai nguồn sóng \(A\) và \(B\) dao động cùng pha với tần số 28 Hz, tốc độ truyền sóng trên mặt nước là 28 cm/s. Khi đó, bước sóng được tính bằng:

Khoảng cách giữa các điểm cực đại sẽ phụ thuộc vào khoảng cách giữa hai nguồn sóng \(d\). Nếu \(d = 5\,\,cm\), số lượng các điểm cực đại sẽ thưa hơn so với trường hợp \(d = 2\,\,cm\).

Do đó, sự điều chỉnh khoảng cách giữa các nguồn sóng là một yếu tố quan trọng để kiểm soát và quan sát rõ ràng các hiện tượng giao thoa trên mặt nước.

Trong mô hình giao thoa sóng trên mặt nước, tính toán công suất sóng có thể được thực hiện dựa trên các yếu tố như bước sóng, tần số, biên độ, và vận tốc sóng. Để hiểu rõ hơn, ta sẽ thực hiện các bước tính toán công suất sóng dựa trên các thông số sau:

1. Xác định bước sóng (\(\lambda\)):

   Bước sóng (\(\lambda\)) là khoảng cách giữa hai điểm tương ứng trên hai gợn sóng kế tiếp nhau. Nó có thể được tính dựa trên tần số (\(f\)) và vận tốc truyền sóng (\(v\)) theo công thức:

   \[
   \lambda = \frac{v}{f}
   \]

2. Tính toán vận tốc truyền sóng (\(v\)):

   Vận tốc truyền sóng có thể được xác định từ các điều kiện thực nghiệm. Ví dụ, trong thí nghiệm giao thoa với hai nguồn sóng kết hợp, nếu tần số dao động là \(15 \, \text{Hz}\) và bước sóng là \(1.2 \, \text{cm}\), vận tốc sóng được tính như sau:

   \[
   v = f \times \lambda = 15 \times 1.2 = 18 \, \text{cm/s}
   \]

3. Xác định biên độ sóng (\(A\)):

   Biên độ sóng là độ cao tối đa mà một phần tử của môi trường dao động khi sóng đi qua. Trong mô hình giao thoa, biên độ tổng hợp tại các điểm cực đại giao thoa có thể là tổng của biên độ từ hai nguồn sóng.

   \[
   A_{\text{max}} = 2A
   \]

4. Tính toán công suất sóng (\(P\)):

   Công suất sóng là năng lượng mà sóng truyền qua một đơn vị diện tích trong một đơn vị thời gian. Nó phụ thuộc vào biên độ, tần số và vận tốc sóng:

   \[
   P = \frac{1}{2} \rho v A^2 f^2
   \]

   Trong đó, \(\rho\) là mật độ của môi trường mà sóng truyền qua, \(v\) là vận tốc sóng, \(A\) là biên độ, và \(f\) là tần số dao động.

5. Áp dụng vào thực tế:

   Giả sử trong thí nghiệm, vận tốc sóng là \(18 \, \text{cm/s}\), biên độ dao động là \(2 \, \text{cm}\), và tần số là \(15 \, \text{Hz}\). Mật độ của nước là \(\rho = 1000 \, \text{kg/m}^3\). Công suất sóng có thể được tính như sau:

   \[
   P = \frac{1}{2} \times 1000 \times 0.18 \times (0.02)^2 \times (15)^2 \approx 1.62 \, \text{W/m}^2
   \]

Như vậy, thông qua các bước trên, ta có thể xác định được công suất sóng dựa trên các thông số thực nghiệm và lý thuyết từ mô hình giao thoa sóng trên mặt nước.

Giao thoa sóng trên mặt nước là một hiện tượng vật lý thú vị và có tính ứng dụng cao trong thực tiễn. Trong lĩnh vực đo đạc thực nghiệm, giao thoa sóng được sử dụng để tiến hành các thí nghiệm chính xác, giúp đo đạc và phân tích sự tương tác giữa các sóng cơ học.

Dưới đây là các bước cơ bản để thực hiện thí nghiệm giao thoa sóng trên mặt nước nhằm ứng dụng vào việc đo đạc:

1. Chuẩn bị thí nghiệm:
   • Chuẩn bị một bể nước nông và trong suốt để dễ quan sát hiện tượng giao thoa.
   • Chuẩn bị các nguồn phát sóng như dao động cơ hoặc thiết bị tạo sóng đều đặn trên mặt nước.
2. Tiến hành thí nghiệm:
   • Khởi động các nguồn phát sóng đồng bộ để tạo ra sóng trên mặt nước.
   • Quan sát các điểm giao thoa của sóng. Những điểm cực đại và cực tiểu xuất hiện tại các vị trí giao thoa sóng.
3. Đo đạc và phân tích:
   • Sử dụng thước đo hoặc công cụ đo lường để xác định khoảng cách giữa các vân giao thoa.
   • Áp dụng công thức giao thoa sóng để tính toán các giá trị cần thiết. Công thức tính khoảng cách giữa các vân giao thoa được xác định bằng: \[ \Delta x = \frac{\lambda D}{d} \] trong đó \( \lambda \) là bước sóng, \( D \) là khoảng cách từ nguồn phát sóng đến màn quan sát, và \( d \) là khoảng cách giữa các nguồn phát sóng.
4. Kết luận:
   • Đưa ra các nhận xét về hiện tượng giao thoa và các kết quả đo đạc. Đối chiếu với lý thuyết để kiểm chứng tính chính xác.

Thí nghiệm này không chỉ giúp sinh viên và nhà nghiên cứu hiểu rõ hơn về bản chất của sóng và hiện tượng giao thoa, mà còn có thể ứng dụng trong các lĩnh vực như kiểm soát sóng trong công nghiệp, nghiên cứu sóng âm trong y học và bảo vệ môi trường nước.

Dạng bài tập này yêu cầu sự kết hợp giữa lý thuyết về giao thoa sóng và kỹ năng giải toán để tìm ra các yếu tố như vị trí giao thoa cực đại, cực tiểu và các thông số liên quan đến bước sóng, tần số và vận tốc sóng.

1. Xác định vị trí các điểm giao thoa

Trong thí nghiệm giao thoa sóng trên mặt nước với hai nguồn sóng kết hợp, ta sử dụng công thức sau để xác định vị trí của các điểm cực đại và cực tiểu:

• Cực đại giao thoa xảy ra khi hiệu đường đi của hai sóng từ hai nguồn đến điểm đang xét là bội số nguyên của bước sóng: \[\Delta d = k \lambda \] (với \(k\) là số nguyên).
• Cực tiểu giao thoa xảy ra khi hiệu đường đi của hai sóng từ hai nguồn đến điểm đang xét là bội số lẻ của nửa bước sóng: \[\Delta d = (k + \frac{1}{2}) \lambda \]

2. Tính toán bước sóng và tần số

Bước sóng và tần số của sóng có thể được tính dựa trên vận tốc sóng và các dữ kiện cho trước:

Trong đó:

• \( \lambda \): Bước sóng (m)
• \( v \): Vận tốc sóng (m/s)
• \( f \): Tần số sóng (Hz)

3. Ví dụ minh họa

Giả sử hai nguồn sóng \(S_1\) và \(S_2\) dao động cùng pha và có khoảng cách \(d = 30 \, cm\). Vận tốc truyền sóng trên mặt nước là \(v = 0.5 \, m/s\), tần số sóng \(f = 25 \, Hz\). Ta có thể tính được bước sóng của sóng là:

Với bước sóng \( \lambda = 0.02 \, m \), ta xác định các vị trí cực đại và cực tiểu dựa trên hiệu đường đi giữa hai nguồn \( S_1 \) và \( S_2 \).

4. Bài tập áp dụng

1. Bài tập 1: Trong thí nghiệm giao thoa, hai nguồn kết hợp dao động với tần số \(f = 24 \, Hz\), vận tốc truyền sóng là \(v = 0.6 \, m/s\). Hãy tính bước sóng và xác định các điểm cực đại và cực tiểu trên mặt nước.
2. Bài tập 2: Trong thí nghiệm với hai nguồn kết hợp cách nhau \(d = 20 \, cm\), tần số sóng là \(f = 30 \, Hz\). Hãy xác định các vị trí điểm cực đại thứ hai và thứ ba từ trung trực của hai nguồn.

5. Kết luận

Việc giải các bài tập về giao thoa sóng trên mặt nước đòi hỏi người học phải nắm vững lý thuyết và biết cách vận dụng công thức để tính toán các đại lượng như bước sóng, tần số và vận tốc sóng. Bằng cách thực hành thường xuyên, học sinh sẽ có thể giải quyết tốt các dạng bài tập tổng hợp này.