Công Thức Nhiễu Xạ Ánh Sáng: Giải Thích, Ứng Dụng và Các Dạng Bài Tập Thực Tế

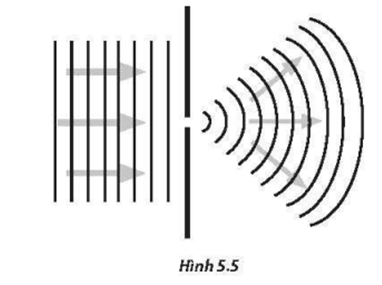
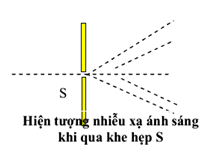
Nhiễu xạ ánh sáng là hiện tượng khi sóng ánh sáng đi qua các vật cản nhỏ hoặc khe hẹp, ánh sáng bị bẻ cong và tạo thành các vân sáng tối xen kẽ nhau. Đây là một minh chứng rõ ràng cho tính chất sóng của ánh sáng. Công thức nhiễu xạ ánh sáng giúp tính toán được vị trí các vân nhiễu xạ trên màn quan sát.

Công Thức Tính Vị Trí Vân Sáng và Vân Tối

Để xác định vị trí của các vân nhiễu xạ trong thí nghiệm với khe hẹp, ta sử dụng công thức:

Trong đó:

• \( d \) là khoảng cách giữa các khe.
• \( \theta \) là góc lệch của vân sáng hoặc vân tối so với trục chính.
• \( m \) là bậc của vân (vân sáng bậc 0, 1, 2,... hoặc vân tối bậc -1, -2,...).
• \( \lambda \) là bước sóng của ánh sáng chiếu vào khe.

Hiện Tượng Nhiễu Xạ Qua Khe Hẹp

Khi ánh sáng đi qua một khe hẹp có độ rộng \( a \), hiện tượng nhiễu xạ xảy ra. Biên độ sáng tối của các vân được phân bố theo công thức:

Trong đó:

• \( I(\theta) \) là cường độ ánh sáng tại góc lệch \( \theta \).
• \( I_0 \) là cường độ sáng tại vân trung tâm (góc \( \theta = 0 \)).
• \( \beta = \frac{\pi a \sin(\theta)}{\lambda} \).

Ví Dụ Thực Tế

Trong thí nghiệm Young với hai khe hẹp, khoảng cách giữa các vân sáng liên tiếp có thể được tính bằng công thức:

Trong đó:

• \( y \) là khoảng cách giữa hai vân sáng hoặc tối liên tiếp trên màn.
• \( L \) là khoảng cách từ khe đến màn quan sát.
• \( d \) là khoảng cách giữa hai khe.
• \( \lambda \) là bước sóng ánh sáng.

Kết Luận

Hiện tượng nhiễu xạ ánh sáng là một minh chứng rõ ràng về tính chất sóng của ánh sáng. Bằng các công thức trên, chúng ta có thể dễ dàng tính toán vị trí và cường độ của các vân sáng tối trong nhiều thí nghiệm khác nhau, từ đó hiểu rõ hơn về bản chất sóng của ánh sáng.

Nhiễu xạ ánh sáng là một hiện tượng quan trọng trong vật lý sóng. Bài viết này sẽ tổng hợp kiến thức cơ bản và các dạng bài tập xoay quanh công thức nhiễu xạ ánh sáng, giúp bạn nắm rõ các khái niệm và ứng dụng của nó trong thực tế.

• 1. Khái Niệm Nhiễu Xạ Ánh Sáng

  Nhiễu xạ ánh sáng là sự uốn cong của sóng ánh sáng khi nó gặp vật cản hoặc đi qua khe hẹp. Hiện tượng này chứng minh rằng ánh sáng có tính chất sóng.

• 2. Công Thức Nhiễu Xạ Ánh Sáng Qua Khe Hẹp

  Công thức tính vị trí các vân sáng, vân tối trong thí nghiệm nhiễu xạ qua khe hẹp được biểu diễn như sau:

  \[ y = \frac{m \cdot \lambda \cdot D}{a} \]

  Trong đó: \( y \) là khoảng cách từ vân sáng (hoặc vân tối) đến trung tâm, \( \lambda \) là bước sóng ánh sáng, \( D \) là khoảng cách từ khe đến màn, và \( a \) là độ rộng của khe.

• 3. Thí Nghiệm Young Với Hai Khe

  Thí nghiệm Young là một minh chứng nổi tiếng về nhiễu xạ và giao thoa ánh sáng, với công thức:

  \[ \Delta y = \frac{\lambda \cdot D}{d} \]

  Trong đó \( \Delta y \) là khoảng cách giữa hai vân sáng liền kề, \( d \) là khoảng cách giữa hai khe.

• 4. Tính Toán Cường Độ Sáng Tại Vị Trí Nhiễu Xạ

  Cường độ sáng tại các vân nhiễu xạ được tính toán dựa trên sự phân bố năng lượng của sóng ánh sáng khi gặp vật cản.

• 5. Ứng Dụng Thực Tế Của Hiện Tượng Nhiễu Xạ Ánh Sáng

  Nhiễu xạ ánh sáng được ứng dụng trong các thiết bị quang học, phân tích vật liệu, và nhiều lĩnh vực khác trong khoa học và công nghệ.

• 6. Bài Tập Vận Dụng Về Nhiễu Xạ Ánh Sáng

  Bài viết cũng cung cấp một số bài tập thực hành liên quan đến nhiễu xạ ánh sáng, giúp bạn củng cố kiến thức.

Trong thí nghiệm nhiễu xạ ánh sáng qua khe hẹp, nhiệm vụ của chúng ta là tính toán vị trí các vân sáng trên màn quan sát dựa vào công thức nhiễu xạ. Bài tập này sẽ hướng dẫn bạn từng bước để xác định vị trí các vân sáng.

1. Bước 1: Xác định các thông số cơ bản

   Trước tiên, chúng ta cần xác định các thông số sau:

   • Độ rộng khe hẹp \( a \)
   • Bước sóng ánh sáng \( \lambda \)
   • Khoảng cách từ khe hẹp đến màn quan sát \( D \)
   • Bậc của vân sáng \( m \) (với \( m = 0, \pm 1, \pm 2, \dots \))
2. Bước 2: Sử dụng công thức tính vị trí các vân sáng

   Công thức tính khoảng cách từ vân sáng trung tâm đến các vân sáng bậc \( m \) là:

   \[ y = \frac{m \cdot \lambda \cdot D}{a} \]

   Trong đó:

   • \( y \) là khoảng cách từ vân sáng trung tâm đến vân sáng bậc \( m \)
   • \( m \) là bậc của vân sáng
   • \( \lambda \) là bước sóng ánh sáng
   • \( D \) là khoảng cách từ khe hẹp đến màn
   • \( a \) là độ rộng của khe
3. Bước 3: Áp dụng công thức

   Giả sử chúng ta có các thông số:

   • \( \lambda = 600 \, \text{nm} \) (bước sóng ánh sáng)
   • \( D = 2 \, \text{m} \) (khoảng cách từ khe hẹp đến màn)
   • \( a = 0.5 \, \text{mm} \) (độ rộng của khe)
   • \( m = 1 \) (bậc của vân sáng)

   Áp dụng công thức:

   \[ y = \frac{1 \cdot 600 \cdot 10^{-9} \cdot 2}{0.5 \cdot 10^{-3}} = 2.4 \, \text{mm} \]
4. Bước 4: Kết luận

   Vị trí của vân sáng bậc 1 so với vân sáng trung tâm là \( y = 2.4 \, \text{mm} \). Bài tập này giúp chúng ta nắm rõ cách áp dụng công thức nhiễu xạ ánh sáng trong thí nghiệm khe hẹp.

Thí nghiệm Young là một trong những thí nghiệm nổi tiếng về hiện tượng giao thoa ánh sáng. Bài tập này sẽ hướng dẫn bạn tính toán khoảng cách giữa các vân sáng trên màn hình quan sát khi tiến hành thí nghiệm giao thoa với hai khe sáng.

1. Bước 1: Xác định các thông số ban đầu

   Trước khi tính toán, chúng ta cần xác định các thông số sau:

   • Bước sóng ánh sáng \( \lambda \)
   • Khoảng cách giữa hai khe \( d \)
   • Khoảng cách từ khe đến màn quan sát \( D \)
2. Bước 2: Sử dụng công thức tính khoảng cách giữa các vân sáng

   Công thức tính khoảng cách giữa hai vân sáng liên tiếp là:

   \[ \Delta y = \frac{\lambda \cdot D}{d} \]

   Trong đó:

   • \( \Delta y \) là khoảng cách giữa hai vân sáng liên tiếp
   • \( \lambda \) là bước sóng ánh sáng
   • \( D \) là khoảng cách từ hai khe đến màn quan sát
   • \( d \) là khoảng cách giữa hai khe
3. Bước 3: Áp dụng công thức với ví dụ cụ thể

   Giả sử chúng ta có các thông số sau:

   • \( \lambda = 500 \, \text{nm} \) (bước sóng ánh sáng)
   • \( D = 1.5 \, \text{m} \) (khoảng cách từ hai khe đến màn)
   • \( d = 0.2 \, \text{mm} \) (khoảng cách giữa hai khe)

   Áp dụng công thức:

   \[ \Delta y = \frac{500 \cdot 10^{-9} \cdot 1.5}{0.2 \cdot 10^{-3}} = 3.75 \, \text{mm} \]
4. Bước 4: Kết luận

   Khoảng cách giữa hai vân sáng liên tiếp trong thí nghiệm Young với các thông số trên là \( 3.75 \, \text{mm} \). Bài tập này giúp chúng ta hiểu rõ hơn về hiện tượng giao thoa ánh sáng và cách tính toán khoảng cách giữa các vân sáng.

Bài tập này hướng dẫn bạn cách xác định bước sóng của ánh sáng thông qua thí nghiệm nhiễu xạ khe hẹp. Chúng ta sẽ sử dụng các thông số thu được từ thí nghiệm để tính toán bước sóng \( \lambda \) của ánh sáng.

1. Bước 1: Xác định các thông số từ thí nghiệm

   Đầu tiên, bạn cần thu thập các thông số sau từ thí nghiệm nhiễu xạ:

   • Khoảng cách từ khe hẹp đến màn quan sát \( D \)
   • Vị trí của vân tối thứ \( n \) \( y_n \) so với vân trung tâm
   • Độ rộng khe hẹp \( a \)
2. Bước 2: Sử dụng công thức nhiễu xạ để tính bước sóng

   Công thức xác định bước sóng \( \lambda \) từ vị trí vân tối trong thí nghiệm nhiễu xạ là:

   \[ \lambda = \frac{y_n \cdot a}{n \cdot D} \]

   Trong đó:

   • \( y_n \) là vị trí của vân tối thứ \( n \) trên màn
   • \( a \) là độ rộng của khe hẹp
   • \( n \) là số thứ tự của vân tối
   • \( D \) là khoảng cách từ khe đến màn
3. Bước 3: Áp dụng công thức vào ví dụ cụ thể

   Giả sử trong một thí nghiệm, chúng ta có các thông số sau:

   • \( y_2 = 4 \, \text{mm} \) (vị trí vân tối thứ 2)
   • \( a = 0.1 \, \text{mm} \) (độ rộng khe)
   • \( n = 2 \) (vân tối thứ 2)
   • \( D = 1 \, \text{m} \) (khoảng cách từ khe đến màn)

   Áp dụng vào công thức:

   \[ \lambda = \frac{4 \cdot 10^{-3} \cdot 0.1 \cdot 10^{-3}}{2 \cdot 1} = 2 \times 10^{-7} \, \text{m} \]

   Vậy bước sóng của ánh sáng là \( 200 \, \text{nm} \).

4. Bước 4: Kết luận

   Thông qua việc đo đạc vị trí của các vân tối trong thí nghiệm nhiễu xạ, ta có thể dễ dàng xác định bước sóng của ánh sáng. Phương pháp này là một minh chứng cho nguyên lý sóng ánh sáng và sự nhiễu xạ.

Trong bài tập này, chúng ta sẽ tính toán cường độ ánh sáng tại một vị trí cụ thể trong thí nghiệm nhiễu xạ ánh sáng. Cường độ ánh sáng có thể được tính dựa trên sự thay đổi pha và biên độ của sóng ánh sáng tại điểm nhiễu xạ.

1. Bước 1: Xác định các thông số cần thiết

   Để tính toán cường độ ánh sáng, chúng ta cần biết các thông số sau:

   • Cường độ ánh sáng tại vân trung tâm \( I_0 \)
   • Góc nhiễu xạ \( \theta \)
   • Bước sóng của ánh sáng \( \lambda \)
   • Độ rộng khe hẹp \( a \)
2. Bước 2: Sử dụng công thức cường độ nhiễu xạ

   Công thức tính cường độ ánh sáng tại vị trí góc nhiễu xạ \( \theta \) là:

   \[ I(\theta) = I_0 \left( \frac{\sin(\beta)}{\beta} \right)^2 \]

   Trong đó:

   • \( \beta = \frac{\pi a \sin(\theta)}{\lambda} \)
   • \( a \) là độ rộng của khe
   • \( \lambda \) là bước sóng ánh sáng
   • \( \theta \) là góc nhiễu xạ
3. Bước 3: Áp dụng công thức vào ví dụ cụ thể

   Giả sử trong một thí nghiệm, chúng ta có các thông số:

   • Cường độ tại vân trung tâm \( I_0 = 1 \, \text{W/m}^2 \)
   • Góc nhiễu xạ \( \theta = 30^\circ \)
   • Bước sóng \( \lambda = 500 \, \text{nm} \)
   • Độ rộng khe \( a = 0.1 \, \text{mm} \)

   Tính \( \beta \):

   \[ \beta = \frac{\pi \cdot 0.1 \cdot 10^{-3} \cdot \sin(30^\circ)}{500 \cdot 10^{-9}} = 314.16 \]

   Sau đó, tính cường độ ánh sáng:

   \[ I(\theta) = 1 \left( \frac{\sin(314.16)}{314.16} \right)^2 \approx 0.01 \, \text{W/m}^2 \]
4. Bước 4: Kết luận

   Cường độ ánh sáng tại góc nhiễu xạ \( 30^\circ \) trong thí nghiệm được tính toán là \( 0.01 \, \text{W/m}^2 \). Điều này cho thấy cường độ giảm mạnh so với cường độ tại vân trung tâm.

Thí nghiệm nhiễu xạ qua khe hẹp là một trong những bài tập quan trọng giúp chúng ta hiểu rõ hơn về tính chất sóng của ánh sáng. Trong bài tập này, chúng ta sẽ tìm hiểu về cách tính toán vị trí và cường độ các vân sáng trong thí nghiệm nhiễu xạ qua khe hẹp.

1. Bước 1: Xác định các thông số cơ bản

   Trong thí nghiệm này, các thông số quan trọng cần xác định bao gồm:

   • Độ rộng của khe hẹp \( a \)
   • Bước sóng của ánh sáng \( \lambda \)
   • Khoảng cách từ khe đến màn quan sát \( D \)
   • Góc nhiễu xạ \( \theta \)
2. Bước 2: Công thức tính vị trí vân sáng và vân tối

   Vị trí của các vân sáng và vân tối có thể được tính bằng công thức nhiễu xạ đơn khe:

   • Vị trí vân sáng:
   \[ y_m = \frac{m \lambda D}{a} \]

   Trong đó:

   • \( m \) là bậc của vân sáng (m = 0, ±1, ±2, ...)
   • \( y_m \) là khoảng cách từ vân trung tâm đến vân sáng bậc m
   • Vị trí vân tối:
   \[ y_n = \frac{(n + 1/2) \lambda D}{a} \]

   Trong đó:

   • \( n \) là bậc của vân tối (n = 0, ±1, ±2, ...)
   • \( y_n \) là khoảng cách từ vân trung tâm đến vân tối bậc n
3. Bước 3: Áp dụng công thức vào ví dụ cụ thể

   Giả sử chúng ta có các thông số sau:

   • Độ rộng khe hẹp \( a = 0.2 \, \text{mm} \)
   • Bước sóng ánh sáng \( \lambda = 600 \, \text{nm} \)
   • Khoảng cách từ khe đến màn \( D = 2 \, \text{m} \)

   Ta có thể tính vị trí vân sáng bậc 1 (m = 1):

   \[ y_1 = \frac{1 \cdot 600 \times 10^{-9} \cdot 2}{0.2 \times 10^{-3}} = 0.006 \, \text{m} = 6 \, \text{mm} \]

   Vậy vân sáng bậc 1 cách vân trung tâm 6 mm.

4. Bước 4: Kết luận

   Thí nghiệm nhiễu xạ qua khe hẹp giúp chúng ta tính toán chính xác vị trí và cường độ của các vân sáng và vân tối trên màn, từ đó khẳng định tính chất sóng của ánh sáng.

Trong hiện tượng nhiễu xạ ánh sáng, việc xác định khoảng cách giữa các vân tối là một phần quan trọng. Đây là bước mà bạn sẽ tính toán dựa trên các công thức đã được thiết lập từ lý thuyết nhiễu xạ qua khe hẹp. Để thực hiện dạng bài tập này, chúng ta sẽ đi qua từng bước một cách chi tiết.

1. Bước 1: Xác định các yếu tố liên quan

   Trước tiên, bạn cần xác định các thông số quan trọng bao gồm:

   • \(a\): Chiều rộng của khe hẹp (đơn vị: mét).
   • \(\lambda\): Bước sóng của ánh sáng sử dụng trong thí nghiệm (đơn vị: mét).
   • \(D\): Khoảng cách từ khe hẹp đến màn quan sát (đơn vị: mét).

2. Bước 2: Sử dụng công thức nhiễu xạ

   Khoảng cách giữa các vân tối có thể được tính dựa vào công thức nhiễu xạ:

   \[
   \Delta y = \frac{\lambda \cdot D}{a}
   \]

   Trong đó:

   • \(\Delta y\): Khoảng cách giữa hai vân tối liên tiếp (đơn vị: mét).
   • \(\lambda\): Bước sóng của ánh sáng.
   • \(D\): Khoảng cách từ khe đến màn.
   • \(a\): Chiều rộng khe hẹp.

3. Bước 3: Thay số và tính toán

   Thay các giá trị cụ thể của \(a\), \(\lambda\), và \(D\) vào công thức trên để tính toán khoảng cách \(\Delta y\) giữa các vân tối. Ví dụ:

   Nếu \(a = 0.1 \, mm\), \(\lambda = 600 \, nm\), và \(D = 1 \, m\), ta có:

   \[
   \Delta y = \frac{600 \times 10^{-9} \, m \times 1 \, m}{0.1 \times 10^{-3} \, m} = 6 \, mm
   \]

4. Bước 4: Phân tích kết quả

   Giá trị \(\Delta y\) sau khi tính toán cho biết khoảng cách giữa hai vân tối liên tiếp trên màn. Để kiểm tra tính chính xác, bạn có thể so sánh kết quả với dữ liệu thực nghiệm hoặc sử dụng các công thức tương tự trong các điều kiện khác.

Như vậy, bằng cách sử dụng công thức nhiễu xạ ánh sáng, chúng ta đã xác định được khoảng cách giữa các vân tối. Đây là một trong những ứng dụng quan trọng của nhiễu xạ trong việc nghiên cứu và phân tích tính chất sóng của ánh sáng.

Trong thí nghiệm Y-âng (Young), hiện tượng giao thoa ánh sáng được sử dụng để xác định khoảng cách giữa các vân sáng trên màn quan sát. Đây là một bài toán phổ biến trong Vật lý về nhiễu xạ ánh sáng, giúp hiểu rõ hơn về tính chất sóng của ánh sáng.

Để tính toán vị trí và khoảng cách giữa các vân sáng, chúng ta sử dụng công thức:

Trong đó:

• \(i\) là khoảng cách giữa hai vân sáng liên tiếp (hay còn gọi là khoảng vân).
• \(\lambda\) là bước sóng của ánh sáng đơn sắc.
• \(D\) là khoảng cách từ khe đến màn quan sát.
• \(a\) là khoảng cách giữa hai khe.

Ví dụ, nếu khoảng cách giữa hai khe là \(a = 2 \, mm\), khoảng cách từ khe đến màn là \(D = 2 \, m\), và bước sóng ánh sáng là \(\lambda = 0.64 \, \mu m\), khoảng vân \(i\) sẽ được tính như sau:

Như vậy, khoảng cách giữa các vân sáng liên tiếp trên màn sẽ là \(0.64 \, mm\).

Để giải quyết bài toán xác định vị trí vân sáng bậc \(n\), công thức được sử dụng là:

Với \(n\) là bậc của vân sáng cần xác định. Chẳng hạn, đối với vân sáng bậc 3:

Như vậy, vân sáng bậc 3 sẽ cách vân trung tâm một khoảng \(1.92 \, mm\) trên màn quan sát.

Trong hiện tượng nhiễu xạ ánh sáng, góc lệch được xác định bằng cách sử dụng các công thức nhiễu xạ cụ thể. Để giải quyết bài tập này, bạn cần tuân theo các bước sau:

1. Bước 1: Xác định bước sóng \(\lambda\) của ánh sáng sử dụng trong thí nghiệm.

   Giả sử ánh sáng có bước sóng \(\lambda\), bạn cần biết giá trị này để tính toán góc lệch.

2. Bước 2: Xác định khoảng cách giữa các khe hẹp (d) trong thí nghiệm nhiễu xạ.

   Giá trị khoảng cách d giữa các khe hẹp được sử dụng để xác định mô hình nhiễu xạ.

3. Bước 3: Sử dụng công thức tính góc lệch trong hiện tượng nhiễu xạ.

   Góc lệch \(\theta\) có thể được xác định thông qua công thức sau:

   \[\sin\theta = \frac{m\lambda}{d}\]

   Trong đó, \(m\) là bậc của vân nhiễu xạ (thường là số nguyên dương).

4. Bước 4: Giải phương trình để tìm góc lệch \(\theta\).

   Bằng cách thay các giá trị của \(\lambda\) và \(d\) vào phương trình trên, bạn có thể tính toán giá trị của \(\theta\) để xác định góc lệch.

5. Bước 5: Phân tích kết quả và đối chiếu với thí nghiệm.

   Sau khi tìm được góc lệch, so sánh kết quả với thực tế hoặc giá trị dự kiến để xác định tính chính xác của phép tính.

Bằng cách thực hiện các bước trên, bạn có thể xác định chính xác góc lệch trong hiện tượng nhiễu xạ ánh sáng, từ đó hiểu rõ hơn về các nguyên lý và công thức liên quan đến nhiễu xạ.

Bước sóng của ánh sáng là một yếu tố quan trọng trong các hiện tượng quang học như nhiễu xạ. Dưới đây là hướng dẫn chi tiết để tính toán bước sóng của ánh sáng đỏ khi nó đi qua hiện tượng nhiễu xạ.

1. Giới thiệu về hiện tượng nhiễu xạ ánh sáng:

Nhiễu xạ xảy ra khi sóng ánh sáng gặp chướng ngại vật hoặc khe hẹp và bị uốn cong, từ đó tạo ra các vân sáng và vân tối trên màn quan sát. Hiện tượng này cho phép xác định bước sóng của ánh sáng thông qua các công thức tính toán dựa trên hình dạng và vị trí của các vân này.

2. Công thức tính bước sóng:

Khi xét hiện tượng nhiễu xạ qua một khe hẹp, bước sóng \(\lambda\) của ánh sáng có thể được tính bằng công thức:

\[
\lambda = \frac{a \cdot y}{m \cdot D}
\]

Trong đó:

• \(\lambda\): Bước sóng của ánh sáng (mét).
• \(a\): Bề rộng của khe hẹp (mét).
• \(y\): Khoảng cách từ vân sáng trung tâm đến vân sáng bậc \(m\) (mét).
• \(m\): Số bậc của vân sáng (thường là một số nguyên dương).
• \(D\): Khoảng cách từ khe hẹp đến màn quan sát (mét).

3. Ví dụ bài tập cụ thể:

Cho một khe hẹp có bề rộng \(a = 0,5 \, mm\), khoảng cách từ khe hẹp đến màn quan sát là \(D = 2 \, m\). Quan sát thấy vân sáng bậc 3 cách vân sáng trung tâm một khoảng \(y = 6 \, mm\). Tính bước sóng của ánh sáng đỏ.

Giải:

Áp dụng công thức tính bước sóng:

\[
\lambda = \frac{0,5 \times 10^{-3} \cdot 6 \times 10^{-3}}{3 \cdot 2} = 5 \times 10^{-7} \, m
\]

Vậy, bước sóng của ánh sáng đỏ là \(500 \, nm\).

4. Kết luận:

Qua bài tập này, ta có thể thấy rằng việc tính toán bước sóng dựa trên hiện tượng nhiễu xạ không chỉ giúp chúng ta hiểu rõ hơn về tính chất sóng của ánh sáng mà còn ứng dụng trong các lĩnh vực nghiên cứu khác nhau, từ vật lý cơ bản đến các công nghệ quang học hiện đại.

Trong hiện tượng nhiễu xạ ánh sáng qua khe hẹp, cường độ ánh sáng tại các vị trí khác nhau trên màn sẽ biến đổi tùy thuộc vào góc quan sát và bước sóng của ánh sáng. Để tính toán cường độ tại vân trung tâm, chúng ta sẽ sử dụng công thức:

Giả sử ánh sáng đơn sắc có bước sóng \(\lambda\) chiếu tới một khe hẹp có bề rộng \(a\). Cường độ sáng tại vân trung tâm (góc \(\theta = 0\)) được xác định bởi:

Trong đó:

• \(I_0\) là cường độ sáng tối đa tại vân trung tâm.
• \(\theta\) là góc lệch so với phương truyền thẳng của ánh sáng.

Khi cần tính cường độ tại một vị trí khác trên màn (tức là khi góc \(\theta\) không bằng 0), ta sử dụng công thức:

Với:

• \(\beta = \frac{\pi a \sin(\theta)}{\lambda}\)

Để tính toán cụ thể, hãy thực hiện các bước sau:

1. Xác định bước sóng ánh sáng \(\lambda\) và bề rộng khe hẹp \(a\).
2. Xác định góc \(\theta\) ứng với vị trí cần tính toán.
3. Tính giá trị \(\beta\) theo công thức: \(\beta = \frac{\pi a \sin(\theta)}{\lambda}\).
4. Áp dụng giá trị \(\beta\) vào công thức cường độ \(I(\theta) = I_0 \left(\frac{\sin(\beta)}{\beta}\right)^2\) để tính cường độ ánh sáng tại vị trí đó.

Ví dụ: Giả sử ánh sáng đỏ có bước sóng \(\lambda = 650 \, nm\) và khe hẹp có bề rộng \(a = 0.2 \, mm\). Tại vân trung tâm (\(\theta = 0\)), cường độ sáng là \(I(0) = I_0\). Với các vị trí khác trên màn, bạn có thể sử dụng công thức trên để tính toán cường độ tương ứng.