Chủ đề nhiễu xạ là gì: Nhiễu xạ là gì? Đây là hiện tượng xảy ra khi sóng bị uốn cong quanh vật cản hoặc qua khe hẹp. Bài viết này sẽ cung cấp một cái nhìn sâu sắc về nhiễu xạ, từ nguyên lý cơ bản đến những ứng dụng quan trọng trong khoa học và công nghệ, giúp bạn hiểu rõ hơn về hiện tượng thú vị này.
Mục lục
- Nhiễu Xạ Là Gì?
- 1. Giới Thiệu Về Nhiễu Xạ
- 2. Các Loại Nhiễu Xạ
- 3. Nguyên Lý Hoạt Động Của Nhiễu Xạ
- 4. Ứng Dụng Của Hiện Tượng Nhiễu Xạ
- 5. Các Bài Tập Về Nhiễu Xạ (Có Lời Giải)
- 5.1. Bài Tập 1: Tính Góc Nhiễu Xạ Theo Định Luật Bragg
- 5.2. Bài Tập 2: Phân Tích Mô Hình Nhiễu Xạ Của Màng Đơn Lớp
- 5.3. Bài Tập 3: Sử Dụng Phép Toán Fourier Trong Nhiễu Xạ
- 5.4. Bài Tập 4: Tính Toán Bước Sóng Dựa Trên Mô Hình Nhiễu Xạ Fraunhofer
- 5.5. Bài Tập 5: Phân Tích Nhiễu Xạ Tia X Để Xác Định Cấu Trúc Tinh Thể
- 5.6. Bài Tập 6: Nghiên Cứu Sự Phân Tán Sóng Âm Qua Khe Hẹp
- 5.7. Bài Tập 7: Ứng Dụng Nhiễu Xạ Trong Thiết Kế Ống Kính Quang Học
- 5.8. Bài Tập 8: Phân Tích Nhiễu Xạ Để Xác Định Thành Phần Hóa Học Của Mẫu
- 5.9. Bài Tập 9: Mô Phỏng Nhiễu Xạ Bằng Phương Pháp Số
- 5.10. Bài Tập 10: Phân Tích Sự Tương Quan Giữa Nhiễu Xạ Và Hiện Tượng Giao Thoa
Nhiễu Xạ Là Gì?
Nhiễu xạ là hiện tượng vật lý xảy ra khi sóng ánh sáng gặp vật cản hoặc khe hẹp và bị bẻ cong, phân tán theo nhiều hướng khác nhau. Hiện tượng này đặc biệt rõ ràng khi kích thước của vật cản hoặc khe có cùng bậc với bước sóng ánh sáng.
1. Khái Niệm Cơ Bản Về Nhiễu Xạ
Nhiễu xạ ánh sáng là hiện tượng mà khi sóng ánh sáng gặp một chướng ngại vật, nó sẽ không chỉ di chuyển theo đường thẳng mà còn có thể uốn cong và lan rộng ra theo các hướng khác nhau. Điều này xảy ra khi ánh sáng gặp phải các vật cản có kích thước nhỏ hơn hoặc tương đương với bước sóng của ánh sáng.
2. Nguyên Lý Hoạt Động Của Nhiễu Xạ
Hiện tượng nhiễu xạ có thể được giải thích bằng nguyên lý Huygens-Fresnel, trong đó mỗi điểm trên mặt sóng được coi là một nguồn phát ra các sóng con. Sự giao thoa giữa các sóng con này sẽ tạo ra các mô hình nhiễu xạ đặc trưng.
Định luật Bragg là một trong những phương pháp cơ bản để phân tích và tính toán các đặc điểm của nhiễu xạ, được biểu diễn bằng công thức:
\[ n\lambda = 2d\sin(\theta) \]
Trong đó:
- \(\lambda\): Bước sóng của ánh sáng
- \(d\): Khoảng cách giữa các mặt phẳng tinh thể
- \(\theta\): Góc nhiễu xạ
- \(n\): Bậc nhiễu xạ (số nguyên)
3. Ứng Dụng Của Hiện Tượng Nhiễu Xạ
- Nhiếp ảnh và nghệ thuật: Sử dụng hiệu ứng nhiễu xạ để tạo ra các hình ảnh độc đáo với sự phân tán ánh sáng, tạo nên không gian nghệ thuật mơ màng.
- Thiết kế ánh sáng: Áp dụng trong việc tạo hiệu ứng ánh sáng trong kiến trúc, sân khấu và sự kiện.
- Kỹ thuật quang học: Sử dụng trong các phương pháp phân tích và đo lường vật liệu, như nhiễu xạ tia X để xác định cấu trúc tinh thể.
- Chẩn đoán y tế: Ứng dụng trong hình ảnh y tế như siêu âm và X-quang để cung cấp hình ảnh chi tiết về cấu trúc cơ thể.
4. Các Loại Nhiễu Xạ
- Nhiễu xạ Fresnel: Xảy ra khi nguồn sáng và màn hình ở khoảng cách hữu hạn so với vật cản.
- Nhiễu xạ Fraunhofer: Xảy ra khi nguồn sáng và màn hình ở rất xa so với vật cản, các sóng ánh sáng coi như song song.
- Nhiễu xạ tia X: Được sử dụng để phân tích cấu trúc tinh thể của vật liệu, giúp xác định các thành phần và đặc điểm của vật liệu ở cấp độ nguyên tử.
5. Tầm Quan Trọng Của Nhiễu Xạ Trong Khoa Học
Hiện tượng nhiễu xạ đóng vai trò quan trọng trong nhiều lĩnh vực nghiên cứu khoa học, từ vật lý, hóa học đến sinh học. Nó giúp các nhà khoa học hiểu rõ hơn về cấu trúc của các vật liệu, đặc tính của sóng ánh sáng, và ứng dụng trong nhiều công nghệ hiện đại.
6. Kết Luận
Nhiễu xạ là một hiện tượng quan trọng và thú vị trong vật lý học, với nhiều ứng dụng thực tiễn trong đời sống và công nghệ. Việc hiểu rõ về nhiễu xạ không chỉ giúp chúng ta khám phá thế giới vi mô mà còn mở ra những khả năng mới trong nhiều lĩnh vực khác nhau.

.png)
1. Giới Thiệu Về Nhiễu Xạ
Nhiễu xạ là một hiện tượng vật lý quan trọng liên quan đến sự uốn cong của sóng khi chúng gặp vật cản hoặc đi qua khe hẹp. Hiện tượng này xuất hiện khi kích thước của vật cản hoặc khe có cùng cỡ với bước sóng của sóng đang truyền. Nhiễu xạ có thể xảy ra với nhiều loại sóng khác nhau như ánh sáng, âm thanh, sóng điện từ, và thậm chí cả sóng nước.
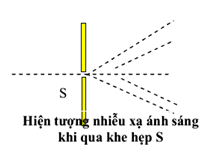
Khi sóng gặp vật cản hoặc đi qua khe hẹp, các phần của sóng sẽ tán xạ ra nhiều hướng khác nhau, dẫn đến sự thay đổi về hướng truyền của sóng. Điều này dẫn đến các hiện tượng như vân nhiễu xạ, nơi ánh sáng hoặc âm thanh tạo ra các mẫu giao thoa phức tạp.
Nguyên lý cơ bản của nhiễu xạ có thể được giải thích bằng lý thuyết sóng Huygens. Theo nguyên lý này, mỗi điểm trên mặt sóng đang lan truyền có thể được coi như là nguồn phát ra các sóng nhỏ. Khi các sóng này giao thoa với nhau, chúng tạo ra các mẫu nhiễu xạ.
Nhiễu xạ không chỉ là một hiện tượng lý thú trong vật lý, mà còn có nhiều ứng dụng thực tiễn trong đời sống. Chẳng hạn, trong quang học, nhiễu xạ được sử dụng để thiết kế các thiết bị như lăng kính nhiễu xạ và các dụng cụ phân tích quang phổ. Trong y học, nhiễu xạ tia X được sử dụng để nghiên cứu cấu trúc tinh thể của các phân tử sinh học, giúp hiểu rõ hơn về cấu trúc của DNA và các protein.
Hiểu rõ hiện tượng nhiễu xạ không chỉ giúp chúng ta nắm vững các nguyên lý cơ bản của sóng, mà còn mở ra nhiều cơ hội ứng dụng trong các lĩnh vực khoa học và công nghệ, từ quang học, âm học, đến công nghệ thông tin và y học.
2. Các Loại Nhiễu Xạ
Nhiễu xạ có thể được chia thành hai loại chính dựa trên đặc điểm và hình dạng của vật cản hoặc khe mà sóng gặp phải. Hai loại nhiễu xạ này là nhiễu xạ Fresnel và nhiễu xạ Fraunhofer.
Nhiễu Xạ Fresnel
Nhiễu xạ Fresnel xảy ra khi sóng truyền qua một vật cản hoặc khe hẹp ở khoảng cách ngắn, tức là khi nguồn sáng và màn quan sát đều nằm gần vật cản. Trong loại nhiễu xạ này, các sóng đi theo những quỹ đạo cong, tạo ra các vân nhiễu xạ không đồng đều trên màn quan sát.
- Đặc điểm: Các vân nhiễu xạ có sự thay đổi về độ sáng và kích thước theo khoảng cách từ vật cản.
- Ứng dụng: Thường được sử dụng trong các nghiên cứu quang học và phân tích cấu trúc của các vật liệu nhỏ.
Nhiễu Xạ Fraunhofer
Nhiễu xạ Fraunhofer xảy ra khi sóng truyền qua vật cản hoặc khe hẹp ở khoảng cách rất xa, khi nguồn sáng và màn quan sát đều nằm ở khoảng cách vô hạn so với vật cản. Trong loại nhiễu xạ này, các sóng đi theo những quỹ đạo thẳng, tạo ra các vân nhiễu xạ đồng đều và dễ dự đoán.
- Đặc điểm: Các vân nhiễu xạ có dạng song song và phân bố đều, giúp dễ dàng phân tích và đo đạc.
- Ứng dụng: Được ứng dụng rộng rãi trong các hệ thống quang học, như trong máy quang phổ và kính hiển vi điện tử.
Cả hai loại nhiễu xạ này đều đóng vai trò quan trọng trong nghiên cứu và ứng dụng thực tiễn, từ việc phân tích vật liệu đến thiết kế các thiết bị quang học phức tạp. Hiểu rõ các loại nhiễu xạ giúp chúng ta áp dụng chúng một cách hiệu quả hơn trong nhiều lĩnh vực khoa học và công nghệ.

3. Nguyên Lý Hoạt Động Của Nhiễu Xạ
Nhiễu xạ xảy ra khi sóng gặp phải một vật cản hoặc khe hẹp, và thay vì đi thẳng, sóng bị bẻ cong và lan tỏa theo các hướng khác nhau. Hiện tượng này được giải thích dựa trên nguyên lý Huygens-Fresnel, cho rằng mỗi điểm trên một mặt sóng có thể coi là nguồn phát ra sóng cầu nhỏ, và sự chồng chập của các sóng cầu này tạo nên hiện tượng nhiễu xạ.
- Khi sóng gặp khe hẹp, các sóng cầu phát ra từ các điểm khác nhau trên khe sẽ giao thoa với nhau, tạo ra các vân sáng và tối trên màn quan sát.
- Độ bẻ cong của sóng phụ thuộc vào kích thước của khe so với bước sóng của sóng tới. Nếu khe hẹp hơn hoặc tương đương với bước sóng, nhiễu xạ sẽ rõ rệt hơn.
- Sự chồng chập của các sóng cầu dẫn đến các khu vực có cường độ sáng khác nhau trên màn quan sát, từ đó tạo thành các vân nhiễu xạ.
Trong nhiễu xạ Fraunhofer, khi nguồn sáng và màn quan sát ở xa vật cản, các sóng cầu trở nên song song, và các vân nhiễu xạ được tạo ra có thể dễ dàng được phân tích dựa trên công thức toán học:
Trong đó, \(\beta = \frac{\pi a \sin(\theta)}{\lambda}\), với \(a\) là độ rộng của khe, \(\lambda\) là bước sóng ánh sáng, và \(\theta\) là góc lệch so với phương truyền thẳng của ánh sáng.
Nhiễu xạ có vai trò quan trọng trong nhiều lĩnh vực như quang học, viễn thông, và phân tích cấu trúc vật liệu. Việc hiểu rõ nguyên lý hoạt động của nhiễu xạ giúp chúng ta ứng dụng hiệu quả trong các công nghệ hiện đại như thiết kế kính hiển vi điện tử, hệ thống quang phổ, và nhiều thiết bị quang học khác.

4. Ứng Dụng Của Hiện Tượng Nhiễu Xạ
Hiện tượng nhiễu xạ, mặc dù thường được liên kết với các hiện tượng quang học, có ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và công nghệ hiện đại. Dưới đây là một số ứng dụng chính của hiện tượng này:
- Thiết Kế Kính Hiển Vi Điện Tử: Nhiễu xạ được sử dụng trong kính hiển vi điện tử để phân tích cấu trúc vi mô của vật liệu. Bằng cách phân tích các mô hình nhiễu xạ, các nhà khoa học có thể xác định cấu trúc nguyên tử của vật liệu với độ chính xác cao.
- Quang Phổ: Nhiễu xạ là cơ sở của nhiều kỹ thuật quang phổ, trong đó có quang phổ nhiễu xạ tia X (XRD) được sử dụng để xác định cấu trúc tinh thể của các chất rắn.
- Hệ Thống Thông Tin Quang Học: Trong viễn thông quang học, nhiễu xạ được tận dụng để kiểm soát và tối ưu hóa việc truyền dẫn ánh sáng qua các sợi quang, từ đó tăng cường hiệu suất và tốc độ truyền thông tin.
- Thiết Kế Màng Mỏng: Các lớp phủ chống phản xạ và các màng mỏng quang học khác được thiết kế dựa trên hiện tượng nhiễu xạ để cải thiện tính năng quang học của các thiết bị như kính mắt, máy ảnh, và ống kính.
- Thiết Kế Cảm Biến: Nhiễu xạ được ứng dụng trong các cảm biến quang học để phát hiện các thay đổi nhỏ trong môi trường, chẳng hạn như sự thay đổi nhiệt độ hoặc áp suất.
Nhìn chung, hiện tượng nhiễu xạ không chỉ giúp chúng ta hiểu rõ hơn về bản chất của ánh sáng và sóng, mà còn mở ra nhiều ứng dụng thiết thực trong các lĩnh vực khác nhau, từ y học, kỹ thuật đến khoa học vật liệu. Khả năng khai thác nhiễu xạ để cải tiến các công nghệ hiện đại đã và đang đóng góp quan trọng vào sự phát triển của khoa học và công nghệ trên toàn cầu.

5. Các Bài Tập Về Nhiễu Xạ (Có Lời Giải)
Dưới đây là danh sách các bài tập về hiện tượng nhiễu xạ cùng với lời giải chi tiết, giúp bạn củng cố kiến thức và hiểu rõ hơn về chủ đề này:
- Bài Tập 1: Tính khoảng cách giữa các vân sáng trong hiện tượng nhiễu xạ qua khe hẹp. \\
- Đề bài: Một khe hẹp có chiều rộng \(a = 0.2\) mm được chiếu bởi ánh sáng đơn sắc có bước sóng \(\lambda = 600\) nm. Khoảng cách từ khe đến màn là \(D = 1\) m. Tính khoảng cách giữa các vân sáng liên tiếp trên màn.
- Lời giải: Ta sử dụng công thức \(x = \frac{\lambda D}{a}\) để tính khoảng cách giữa các vân sáng: \[ x = \frac{600 \times 10^{-9} \times 1}{0.2 \times 10^{-3}} = 3 \times 10^{-3} \, \text{m} = 3 \, \text{mm} \] Vậy khoảng cách giữa các vân sáng là 3 mm.
- Bài Tập 2: Tính góc nhiễu xạ bậc nhất cho hiện tượng nhiễu xạ qua cách tử. \\
- Đề bài: Một cách tử có 5000 vạch/mm được chiếu sáng bởi ánh sáng có bước sóng \(\lambda = 650\) nm. Tính góc nhiễu xạ bậc nhất.
- Lời giải: Ta sử dụng công thức \(d \sin \theta = m\lambda\), với \(d = \frac{1}{5000} \, \text{mm} = 2 \times 10^{-4}\) mm: \[ \sin \theta = \frac{1 \times 650 \times 10^{-9}}{2 \times 10^{-4}} = 3.25 \times 10^{-3} \] \(\theta \approx 0.186^\circ\).
- Bài Tập 3: Xác định bước sóng của ánh sáng qua hiện tượng nhiễu xạ. \\
- Đề bài: Khi ánh sáng đơn sắc đi qua một khe hẹp có chiều rộng \(a = 0.1\) mm, góc lệch của vân tối bậc nhất là \(2^\circ\). Xác định bước sóng của ánh sáng.
- Lời giải: Sử dụng công thức \(a \sin \theta = m\lambda\), với \(m = 1\), ta có: \[ \lambda = \frac{a \sin \theta}{m} = 0.1 \times 10^{-3} \times \sin 2^\circ = 3.49 \times 10^{-7} \, \text{m} = 349 \, \text{nm} \] Vậy bước sóng của ánh sáng là 349 nm.
- Bài Tập 4: Tính khoảng cách từ màn đến khe trong hiện tượng nhiễu xạ qua khe kép. \\
- Đề bài: Ánh sáng đơn sắc có bước sóng \(\lambda = 500\) nm đi qua một khe kép có khoảng cách giữa hai khe là \(d = 0.3\) mm. Khoảng cách giữa hai vân sáng liên tiếp trên màn là 2 mm. Tính khoảng cách từ màn đến khe.
- Lời giải: Ta sử dụng công thức \(x = \frac{\lambda D}{d}\) để tính khoảng cách \(D\): \[ D = \frac{x \times d}{\lambda} = \frac{2 \times 10^{-3} \times 0.3 \times 10^{-3}}{500 \times 10^{-9}} = 1.2 \, \text{m} \] Vậy khoảng cách từ màn đến khe là 1.2 m.
- Bài Tập 5: Tính cường độ sáng tại điểm trên màn trong hiện tượng nhiễu xạ qua khe đơn. \\
- Đề bài: Ánh sáng có bước sóng \(\lambda = 450\) nm đi qua khe đơn có chiều rộng \(a = 0.05\) mm. Tính cường độ sáng tại một điểm trên màn với góc lệch \(\theta = 1^\circ\) so với trục chính.
- Lời giải: Cường độ sáng được tính theo công thức: \[ I(\theta) = I_0 \left( \frac{\sin(\beta)}{\beta} \right)^2 \] Với \(\beta = \frac{\pi a \sin \theta}{\lambda}\), thay các giá trị vào: \[ \beta = \frac{\pi \times 0.05 \times 10^{-3} \times \sin 1^\circ}{450 \times 10^{-9}} = 0.109 \] Cường độ sáng tại điểm cần tính: \[ I(\theta) = I_0 \left( \frac{\sin(0.109)}{0.109} \right)^2 \approx 0.996 I_0 \]
XEM THÊM:
5.1. Bài Tập 1: Tính Góc Nhiễu Xạ Theo Định Luật Bragg
Định luật Bragg là một trong những công cụ quan trọng trong việc phân tích nhiễu xạ tia X, được sử dụng để tính toán góc nhiễu xạ khi biết khoảng cách giữa các mặt phẳng nguyên tử và bước sóng của tia X.
Bài tập: Cho một tinh thể có các mặt phẳng nguyên tử cách nhau một khoảng \(d = 2.5 \, \text{Å}\). Tia X chiếu tới với bước sóng \(\lambda = 1.54 \, \text{Å}\). Tính góc nhiễu xạ đầu tiên (góc Bragg) xuất hiện trong quá trình nhiễu xạ.
Lời giải:
- Áp dụng định luật Bragg, ta có công thức: \[ n\lambda = 2d\sin\theta \] Với \(n\) là số nguyên dương (thứ tự của cực đại), \(\lambda\) là bước sóng của tia X, \(d\) là khoảng cách giữa các mặt phẳng nguyên tử, và \(\theta\) là góc nhiễu xạ.
- Trong trường hợp này, để tính góc nhiễu xạ đầu tiên, ta chọn \(n = 1\). Thay các giá trị đã biết vào công thức: \[ 1.54 = 2 \times 2.5 \times \sin\theta \]
- Giải phương trình trên để tìm \(\sin\theta\): \[ \sin\theta = \frac{1.54}{5} = 0.308 \]
- Dùng máy tính để tìm góc \(\theta\): \[ \theta = \arcsin(0.308) \approx 17.98^\circ \]
- Vậy góc nhiễu xạ đầu tiên xuất hiện là \(\theta \approx 17.98^\circ\).
Qua bài tập này, chúng ta thấy rằng định luật Bragg giúp ta xác định chính xác góc nhiễu xạ, điều này rất quan trọng trong việc phân tích cấu trúc tinh thể bằng tia X.
5.2. Bài Tập 2: Phân Tích Mô Hình Nhiễu Xạ Của Màng Đơn Lớp
Trong bài tập này, chúng ta sẽ phân tích mô hình nhiễu xạ của một màng đơn lớp mỏng bằng cách sử dụng nguyên lý nhiễu xạ ánh sáng. Quá trình này liên quan đến việc tính toán và giải thích các kết quả nhiễu xạ thu được từ một chùm tia sáng đi qua màng đơn lớp. Dưới đây là các bước thực hiện:
- Bước 1: Xác định các tham số cần thiết để mô phỏng nhiễu xạ. Gọi \( d \) là khoảng cách giữa các lớp của màng, \( \lambda \) là bước sóng của ánh sáng chiếu vào màng.
- Bước 2: Sử dụng nguyên lý Huygens-Fresnel để mô tả cách thức mỗi điểm trên màng trở thành một nguồn phát sóng thứ cấp. Các sóng này giao thoa với nhau để tạo ra mô hình nhiễu xạ.
- Bước 3: Áp dụng định luật Bragg cho màng đơn lớp để tìm các góc nhiễu xạ thoả mãn điều kiện:
- Trong đó, \( n \) là số nguyên biểu diễn bậc của nhiễu xạ, \( \theta \) là góc nhiễu xạ. Công thức này cho phép tính toán góc tại đó nhiễu xạ xảy ra.
- Bước 4: Mô phỏng và vẽ đồ thị mô hình nhiễu xạ dựa trên các góc tính được từ bước 3. Dữ liệu này có thể được sử dụng để so sánh với các kết quả thực nghiệm.
- Bước 5: Phân tích kết quả nhiễu xạ thu được và đưa ra kết luận về tính chất của màng đơn lớp, bao gồm độ dày của màng và các tính chất quang học liên quan.
\[ n\lambda = 2d \sin \theta \]
Bài tập này giúp sinh viên hiểu rõ hơn về cơ chế của nhiễu xạ trong màng đơn lớp và cách áp dụng lý thuyết vào thực tế. Việc thực hiện mô phỏng và phân tích các góc nhiễu xạ sẽ cung cấp cái nhìn sâu sắc về cấu trúc của màng và các hiện tượng quang học liên quan.

5.3. Bài Tập 3: Sử Dụng Phép Toán Fourier Trong Nhiễu Xạ
Trong bài tập này, chúng ta sẽ áp dụng phép toán Fourier để phân tích hiện tượng nhiễu xạ ánh sáng. Nhiễu xạ xảy ra khi ánh sáng đi qua một vật cản hoặc khe hẹp, làm thay đổi hướng truyền thẳng của sóng ánh sáng và dẫn đến hiện tượng giao thoa. Để hiểu rõ hơn về quá trình này, chúng ta sẽ đi sâu vào các bước thực hiện sau:
-
Bước 1: Xác định hàm truyền của hệ thống
Khi ánh sáng gặp một vật cản hoặc khe hẹp, nó sẽ tạo ra một mô hình nhiễu xạ trên màn hứng. Mô hình này có thể được mô tả bằng một hàm truyền \( T(x) \) đặc trưng cho hệ thống nhiễu xạ.
-
Bước 2: Áp dụng phép biến đổi Fourier
Để tính toán phân bố cường độ ánh sáng trên màn hứng, chúng ta sử dụng phép biến đổi Fourier. Phép biến đổi Fourier của hàm truyền \( T(x) \) sẽ cho chúng ta biểu thức toán học của mô hình nhiễu xạ:
\[
I(k) = \left| \mathcal{F}\{T(x)\} \right|^2
\]Trong đó, \( I(k) \) là cường độ ánh sáng tại vị trí \( k \) trên màn, và \( \mathcal{F} \) là phép biến đổi Fourier.
-
Bước 3: Phân tích kết quả
Dựa trên biểu thức nhận được từ phép biến đổi Fourier, chúng ta có thể phân tích các đặc điểm của mô hình nhiễu xạ, chẳng hạn như vị trí của các vân sáng và vân tối, cũng như cường độ của chúng.
Ví dụ, nếu chúng ta có một khe đơn với hàm truyền \( T(x) \) là một hàm chữ nhật, phép biến đổi Fourier sẽ cho chúng ta một mô hình nhiễu xạ có dạng hàm \( sinc \), với các cực đại và cực tiểu tương ứng với các vân sáng và vân tối trên màn.
-
Bước 4: So sánh với thí nghiệm thực tế
Cuối cùng, so sánh kết quả lý thuyết từ phép toán Fourier với các kết quả thí nghiệm để xác nhận tính chính xác và hiệu quả của phương pháp. Điều này giúp chúng ta hiểu sâu hơn về bản chất sóng của ánh sáng và hiện tượng nhiễu xạ.
Bài tập này không chỉ giúp bạn nắm vững cách sử dụng phép toán Fourier trong phân tích nhiễu xạ, mà còn cung cấp một cái nhìn sâu sắc về các hiện tượng quang học liên quan.
5.4. Bài Tập 4: Tính Toán Bước Sóng Dựa Trên Mô Hình Nhiễu Xạ Fraunhofer
Trong bài tập này, chúng ta sẽ tìm hiểu và áp dụng phép toán Fourier để tính toán bước sóng ánh sáng dựa trên mô hình nhiễu xạ Fraunhofer. Nhiễu xạ là hiện tượng ánh sáng bị bẻ cong khi đi qua một vật cản hoặc khe hẹp, làm cho ánh sáng không còn đi theo đường thẳng mà phân tán ra các hướng khác nhau.
- Bước 1: Đầu tiên, hãy xem xét một khe hẹp có độ rộng \( a \). Khi ánh sáng đơn sắc có bước sóng \( \lambda \) chiếu qua khe này, ta sẽ quan sát được một mẫu nhiễu xạ trên màn.
- Bước 2: Sử dụng mô hình nhiễu xạ Fraunhofer, ta có thể biểu diễn cường độ ánh sáng trên màn theo công thức Fourier:
\[
I(\theta) = I_0 \left( \frac{\sin(\beta)}{\beta} \right)^2
\]
Với:
- \( I_0 \): Cường độ ánh sáng tại điểm chính giữa
- \( \beta = \frac{\pi a \sin(\theta)}{\lambda} \)
- \( \theta \): Góc nhiễu xạ
- Bước 3: Để tính toán bước sóng \( \lambda \), ta có thể sử dụng vị trí của các cực tiểu nhiễu xạ trên màn. Cực tiểu thứ nhất xảy ra khi \( \beta = \pm \pi \), do đó ta có phương trình:
\[
\sin(\theta_1) = \frac{\lambda}{a}
\]
- Bước 4: Từ phương trình trên, suy ra công thức tính bước sóng \( \lambda \):
\[
\lambda = a \sin(\theta_1)
\]
- Bước 5: Bây giờ, bạn có thể đo góc \( \theta_1 \) từ thực nghiệm và sử dụng công thức trên để tính toán bước sóng ánh sáng \( \lambda \).
Thông qua bài tập này, bạn đã học được cách áp dụng mô hình nhiễu xạ Fraunhofer để xác định bước sóng của ánh sáng một cách chính xác.

5.5. Bài Tập 5: Phân Tích Nhiễu Xạ Tia X Để Xác Định Cấu Trúc Tinh Thể
Nhiễu xạ tia X là một phương pháp phân tích không phá hủy, được sử dụng rộng rãi trong việc xác định cấu trúc tinh thể của các vật liệu. Dưới đây là các bước cơ bản để thực hiện bài tập phân tích nhiễu xạ tia X nhằm xác định cấu trúc tinh thể:
- Bước 1: Chuẩn bị mẫu
Chọn mẫu vật liệu cần phân tích. Mẫu cần phải có kích thước và hình dạng phù hợp để đảm bảo tia X có thể chiếu xuyên qua một cách hiệu quả.
- Bước 2: Chiếu tia X
Chiếu một chùm tia X đơn sắc vào mẫu vật liệu. Khi tia X đi qua mẫu, nó sẽ tương tác với các nguyên tử trong cấu trúc tinh thể và gây ra hiện tượng nhiễu xạ.
- Bước 3: Ghi nhận mô hình nhiễu xạ
Đo góc và cường độ của các đỉnh nhiễu xạ trên màn ghi nhận. Các đỉnh này tương ứng với sự phân bố của các nguyên tử trong mạng tinh thể của mẫu.
- Bước 4: Phân tích dữ liệu
So sánh các đỉnh nhiễu xạ thu được với cơ sở dữ liệu chuẩn (ví dụ: ICDD - Trung tâm Quốc tế về Dữ liệu nhiễu xạ) để xác định các pha của mẫu. Kích thước tinh thể trung bình và các khuyết tật trong cấu trúc cũng có thể được xác định từ mô hình nhiễu xạ.
- Bước 5: Kết luận
Sử dụng kết quả phân tích để đưa ra kết luận về cấu trúc tinh thể của mẫu, bao gồm việc xác định loại tinh thể, kích thước ô mạng và các đặc điểm đặc trưng khác.
Dưới đây là một số công thức liên quan đến nhiễu xạ tia X:
- Công thức Bragg: \[n\lambda = 2d\sin\theta\], trong đó:
- \(\lambda\) là bước sóng của tia X.
- \(d\) là khoảng cách giữa các mặt phẳng trong mạng tinh thể.
- \(\theta\) là góc nhiễu xạ.
- \(n\) là số nguyên bậc nhiễu xạ.
- Cường độ của các đỉnh nhiễu xạ: \[I(hkl) \propto \frac{1}{V^2} \left|F(hkl)\right|^2\], với:
- \(I(hkl)\) là cường độ đỉnh nhiễu xạ ứng với mặt phẳng \(hkl\).
- \(V\) là thể tích ô mạng đơn vị.
- \(F(hkl)\) là yếu tố cấu trúc của mặt phẳng \(hkl\).
5.6. Bài Tập 6: Nghiên Cứu Sự Phân Tán Sóng Âm Qua Khe Hẹp
Trong bài tập này, chúng ta sẽ nghiên cứu hiện tượng phân tán sóng âm khi đi qua một khe hẹp. Hiện tượng này có thể được giải thích bằng hiện tượng nhiễu xạ, một hiện tượng thường gặp khi sóng truyền qua các vật cản hoặc khe hẹp.
Đầu tiên, hãy xem xét nguyên lý cơ bản của sự nhiễu xạ. Khi sóng âm truyền qua một khe hẹp, nó không chỉ đi thẳng qua khe mà còn lan rộng ra hai phía của khe. Sự lan rộng này gây ra hiện tượng giao thoa, tức là sự chồng chập của các sóng. Kết quả là, phía sau khe hẹp sẽ có những vùng giao thoa sáng tối xen kẽ nhau, tùy thuộc vào tần số và bước sóng của sóng âm.
Để mô phỏng và hiểu rõ hơn về hiện tượng này, chúng ta sẽ thực hiện các bước sau:
- Chuẩn bị: Chuẩn bị nguồn phát sóng âm, một khe hẹp có thể điều chỉnh độ rộng, và các thiết bị đo đạc cần thiết như micro và máy hiện sóng.
- Thí nghiệm:
- Đặt nguồn phát sóng âm cách khe hẹp một khoảng cách nhất định.
- Điều chỉnh độ rộng của khe và quan sát sự thay đổi trong mẫu phân tán của sóng âm phía sau khe.
- Sử dụng micro để thu thập dữ liệu sóng âm tại các vị trí khác nhau phía sau khe, ghi lại cường độ và pha của sóng âm tại các điểm đó.
- Phân tích:
- Sử dụng các công cụ toán học để phân tích mẫu giao thoa thu được, tính toán các vị trí cực đại và cực tiểu của cường độ sóng.
- Sử dụng công thức nhiễu xạ \[ a \sin(\theta) = m \lambda \] để tính toán và so sánh với dữ liệu thực nghiệm.
- Kết luận: Rút ra kết luận về sự ảnh hưởng của độ rộng khe đến sự phân tán sóng âm, cũng như mối quan hệ giữa tần số sóng, bước sóng, và góc nhiễu xạ.
Bằng việc hoàn thành bài tập này, bạn sẽ hiểu rõ hơn về cách sóng âm phân tán qua khe hẹp và ứng dụng của hiện tượng nhiễu xạ trong các tình huống thực tế, chẳng hạn như trong thiết kế các hệ thống âm thanh và nghiên cứu về âm học.
| Bước | Mô tả |
| Bước 1 | Chuẩn bị các thiết bị và dụng cụ cần thiết. |
| Bước 2 | Thực hiện thí nghiệm bằng cách phát sóng âm qua khe hẹp và thu thập dữ liệu. |
| Bước 3 | Phân tích dữ liệu và so sánh với lý thuyết. |
| Bước 4 | Rút ra kết luận và ứng dụng thực tế. |
5.7. Bài Tập 7: Ứng Dụng Nhiễu Xạ Trong Thiết Kế Ống Kính Quang Học
Trong bài tập này, chúng ta sẽ tìm hiểu cách nhiễu xạ ánh sáng có thể được ứng dụng trong việc thiết kế ống kính quang học, giúp cải thiện chất lượng hình ảnh và giảm thiểu các sai lệch quang học.
- Bước 1: Xem xét sự tương tác giữa ánh sáng và các cấu trúc quang học của ống kính. Khi ánh sáng đi qua các lỗ nhỏ hoặc khe hẹp, hiện tượng nhiễu xạ xảy ra, làm thay đổi hướng đi của sóng ánh sáng.
- Bước 2: Áp dụng phép toán Fourier để phân tích các mẫu nhiễu xạ. Phép toán này giúp biểu diễn hình ảnh quang học thành các tần số không gian, cho phép chúng ta hiểu rõ hơn về cách mà nhiễu xạ ảnh hưởng đến hình ảnh thu được.
- Bước 3: Dựa trên các phân tích từ bước 2, điều chỉnh thiết kế của ống kính để tối ưu hóa hiệu suất quang học. Điều này có thể bao gồm việc thay đổi kích thước và hình dạng của các phần tử trong ống kính nhằm kiểm soát tốt hơn nhiễu xạ.
- Bước 4: Sử dụng mô hình nhiễu xạ Fraunhofer để tính toán bước sóng ánh sáng liên quan và xác định cấu trúc quang học phù hợp cho ống kính.
Để thực hiện các tính toán trên, bạn có thể áp dụng các công thức sau:
- Công thức tính khoảng vân nhiễu xạ: \[ i = \frac{\lambda D}{a} \], trong đó:
- \( \lambda \) là bước sóng ánh sáng,
- \( D \) là khoảng cách từ khe nhiễu xạ đến màn quan sát,
- \( a \) là khoảng cách giữa hai khe nhiễu xạ.
- Công thức tính cường độ nhiễu xạ: \[ I(\theta) = I_0 \left(\frac{\sin(\beta)}{\beta}\right)^2 \], với \( \beta = \frac{\pi a \sin(\theta)}{\lambda} \).
Qua bài tập này, bạn sẽ hiểu rõ hơn về cách hiện tượng nhiễu xạ được sử dụng trong thực tế để cải thiện thiết kế và hiệu năng của các hệ thống quang học.
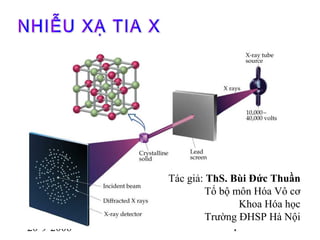
5.8. Bài Tập 8: Phân Tích Nhiễu Xạ Để Xác Định Thành Phần Hóa Học Của Mẫu
Trong bài tập này, chúng ta sẽ tìm hiểu về ứng dụng của nhiễu xạ trong việc xác định thành phần hóa học của mẫu. Nhiễu xạ là hiện tượng mà sóng ánh sáng hoặc sóng khác bị bẻ cong khi chúng đi qua một lỗ nhỏ hoặc gặp chướng ngại vật, tạo ra các mẫu giao thoa đặc trưng.
Trong phân tích nhiễu xạ tia X (XRD), một chùm tia X được chiếu vào mẫu vật liệu. Các nguyên tử trong mẫu sẽ làm tán xạ chùm tia X này, dẫn đến sự hình thành các mẫu giao thoa nhiễu xạ đặc trưng. Dựa trên các mẫu này, chúng ta có thể xác định được các khoảng cách giữa các lớp nguyên tử trong tinh thể, từ đó suy ra các thành phần hóa học có trong mẫu.
- Bước 1: Chuẩn bị mẫu vật liệu cần phân tích. Mẫu cần phải ở dạng tinh thể hoặc ít nhất có cấu trúc tinh thể rõ ràng để đảm bảo kết quả nhiễu xạ chính xác.
- Bước 2: Sử dụng máy XRD để chiếu tia X vào mẫu. Máy sẽ đo các góc tán xạ và cường độ của các chùm tia X bị nhiễu xạ.
- Bước 3: Phân tích các dữ liệu thu thập được để xác định các khoảng cách giữa các lớp nguyên tử trong mẫu. Dữ liệu này thường được biểu diễn dưới dạng các đồ thị nhiễu xạ với các đỉnh đặc trưng.
- Bước 4: So sánh các đỉnh nhiễu xạ với cơ sở dữ liệu chuẩn để xác định các thành phần hóa học có trong mẫu. Mỗi hợp chất hóa học có một mẫu nhiễu xạ riêng biệt, giúp chúng ta dễ dàng nhận diện chúng.
Ứng dụng của nhiễu xạ trong phân tích hóa học không chỉ dừng lại ở việc xác định thành phần, mà còn giúp kiểm tra độ tinh khiết của vật liệu, đánh giá cấu trúc và các khuyết tật trong tinh thể. Điều này đặc biệt hữu ích trong ngành công nghiệp vật liệu và nghiên cứu khoa học.
Ví dụ, trong việc phân tích thành phần hóa học của hợp kim thép, kỹ thuật XRD cho phép xác định các pha cấu trúc khác nhau trong hợp kim, từ đó đưa ra những đánh giá về tính chất cơ lý của vật liệu.
| Công thức tổng quát: | \[d = \frac{n\lambda}{2\sin\theta}\] |
| Trong đó: |
|
5.9. Bài Tập 9: Mô Phỏng Nhiễu Xạ Bằng Phương Pháp Số
Trong bài tập này, chúng ta sẽ nghiên cứu và mô phỏng hiện tượng nhiễu xạ thông qua phương pháp số. Nhiễu xạ là hiện tượng xảy ra khi sóng đi qua một khe hẹp hoặc gặp một chướng ngại vật, làm cho sóng bị uốn cong và tạo ra các mô hình giao thoa phức tạp. Phương pháp số sẽ giúp chúng ta hiểu rõ hơn về sự lan truyền và tương tác của sóng trong các môi trường khác nhau.
- Bước 1: Xây dựng mô hình toán học
- Bước 2: Chọn phương pháp số phù hợp
- Bước 3: Triển khai mô phỏng trên máy tính
- Bước 4: Phân tích kết quả
Đầu tiên, cần thiết lập các phương trình mô tả sự truyền sóng trong không gian, bao gồm cả điều kiện biên và các yếu tố tác động như khe hẹp hay chướng ngại vật. Một trong những phương trình cơ bản nhất là phương trình Helmholtz:
\[ \nabla^2 U + k^2 U = 0 \]trong đó, \(U\) là biên độ của sóng và \(k\) là số sóng.
Phương pháp số phổ biến được sử dụng để giải các phương trình này là phương pháp phần tử hữu hạn (FEM) hoặc phương pháp sai phân hữu hạn (FDM). Các phương pháp này cho phép chúng ta chia nhỏ không gian thành các phần tử hoặc điểm lưới để tính toán sự lan truyền sóng một cách chính xác.
Sử dụng phần mềm chuyên dụng hoặc các ngôn ngữ lập trình như Python, MATLAB để mô phỏng sự lan truyền sóng và hiện tượng nhiễu xạ. Kết quả mô phỏng sẽ giúp chúng ta hình dung rõ hơn về các mô hình nhiễu xạ, bao gồm các vùng sáng-tối trong mô hình giao thoa.
Cuối cùng, phân tích các kết quả mô phỏng để xác định các yếu tố ảnh hưởng đến hiện tượng nhiễu xạ, như kích thước khe hẹp, tần số sóng, và góc tới. Điều này giúp rút ra các kết luận quan trọng về sự phân bố năng lượng và cường độ của sóng sau khi nhiễu xạ.
Bài tập này không chỉ giúp bạn nắm vững kiến thức về nhiễu xạ mà còn phát triển kỹ năng ứng dụng toán học và phương pháp số vào việc giải quyết các vấn đề vật lý phức tạp.
5.10. Bài Tập 10: Phân Tích Sự Tương Quan Giữa Nhiễu Xạ Và Hiện Tượng Giao Thoa
Trong bài tập này, chúng ta sẽ đi sâu vào phân tích sự tương quan giữa hai hiện tượng nhiễu xạ và giao thoa, vốn là những hiện tượng quan trọng trong quang học sóng. Cả hai hiện tượng này đều liên quan đến tính chất sóng của ánh sáng, nhưng chúng có những đặc điểm riêng biệt và ứng dụng cụ thể.
Bước 1: Hiểu hiện tượng nhiễu xạ
Nhiễu xạ là hiện tượng khi sóng ánh sáng đi qua một vật cản hoặc khe hẹp, nó bị uốn cong và lan rộng ra. Hiện tượng này chứng tỏ ánh sáng có tính chất sóng. Để giải thích rõ hơn, ta xét trường hợp ánh sáng đi qua một khe hẹp và tạo ra các vân nhiễu xạ, với các vân sáng và tối xen kẽ nhau.
Bước 2: Hiểu hiện tượng giao thoa
Giao thoa là hiện tượng xảy ra khi hai sóng ánh sáng kết hợp với nhau, tạo ra các vân sáng và tối do sự cộng hưởng hoặc triệt tiêu lẫn nhau. Giao thoa có thể xảy ra với các sóng có cùng bước sóng và pha, và được ứng dụng trong nhiều thiết bị quang học như giao thoa kế.
Bước 3: So sánh và phân tích sự tương quan
Để so sánh hai hiện tượng này, ta cần phân tích các điểm tương đồng và khác biệt:
- Cả nhiễu xạ và giao thoa đều liên quan đến sự can thiệp của sóng, dẫn đến sự hình thành các vân sáng tối.
- Nhiễu xạ xảy ra khi sóng đi qua vật cản hoặc khe hẹp, còn giao thoa xảy ra khi hai sóng gặp nhau.
- Các vân nhiễu xạ thường lan rộng ra không gian, trong khi các vân giao thoa có thể được điều chỉnh bởi khoảng cách giữa hai nguồn sáng.
Bước 4: Ứng dụng thực tiễn
Hiểu rõ sự tương quan giữa nhiễu xạ và giao thoa giúp chúng ta thiết kế các thiết bị quang học chính xác hơn. Ví dụ, trong thiết kế ống kính quang học, việc kiểm soát nhiễu xạ và giao thoa giúp giảm thiểu sai số và nâng cao chất lượng hình ảnh.
Bước 5: Bài tập thực hành
Sử dụng các phương trình sau để mô phỏng các vân sáng tối trong nhiễu xạ và giao thoa:
- Vân sáng tối trong nhiễu xạ: \(\theta = \frac{m\lambda}{a}\) với \(m = 0, \pm 1, \pm 2,...\)
- Vân sáng tối trong giao thoa: \(\Delta \phi = \frac{2\pi d}{\lambda}\)
Hãy áp dụng các công thức này vào việc mô phỏng trên máy tính, so sánh kết quả thu được và rút ra kết luận về sự tương quan giữa hai hiện tượng này.